Системы координат, используемые в трехмерном моделировании

В приложениях трехмерной графики, в зависимости от решаемых задач, используются как минимум двумя системами координат. Для задания координат точек в трехмерном пространстве модели «мира» будем использовать общепринятую в векторной алгебре правую систему координат (рис. 3.1 а). При этом, если смотреть со стороны положительной полуоси в центр координат, то поворот на +90° (против часовой стрелке) переводит одну положительную ось в другую (направление движения расположенного вдоль оси и поворачивающегося против часовой стрелки правого винта и положительной полуоси совпадают).

Рис. 3.1. Правая (а) и левая (б) системы координат.

Для представления координат точек в системе связанной с плоскостью экрана, будет использоваться левая система координат (см. рис. 3.1 б). При этом плоскость экрана совмещается с плоскостью XY, а ось z направлена в глубь экрана. В левой системе координат положительными будут повороты по часовой стрелке, если смотреть с положительного конца полуоси.

Геометрические преобразования в пространстве.

Как и на плоскости, так и в трехмерном пространстве любое преобразование координат точек или изменение системы координат можно представить в виде совокупности элементарных преобразований переноса, поворота относительно координатных осей и масштабирования. Матрицы для этих преобразований в системе однородных координат следующие:

1. Перенос точки на расстояния , вдоль положительных направлений осей 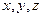соответственно, либо перенос начала системы координат на расстояния , вдоль отрицательных направлений осей 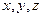соответственно:

.

2. Поворот точек плоскости на угол вокруг оси OZ, либо поворот осей системы координат вокруг оси OZ на угол :

.

3. Поворот точек плоскости на угол вокруг оси OX, либо поворот осей системы координат вокруг оси OX на угол :

.

4. Поворот точек плоскости на угол вокруг оси OY, либо поворот осей системы координат вокруг оси OY на угол :

.

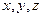5. Масштабирование координат точек плоскости относительно начала системы координат в раз, по координатам соответственно, либо базовых векторов в раз соответственно:

Видовое преобразование.

В данной работе используется представление объектов сцены в виде каркасных (проволочных моделей). При этом каждый объект сцены задается наборами своих вершин и ребер. Вершины задаются своими трехмерными координатами в системе модели «мира». Будем называть такую систему мировой, а координаты - мировыми. Каждое ребро объекта будет определяться двумя вершинами, т.е. представлять собой отрезок прямой линии, соединяющий две вершины рис. 3.2.

Рис.3.2. Вершины и ребра каркасной модели объекта

Для того чтобы получить изображение объекта, как он выглядит при наблюдении из некоторой точки, необходимо знать:

1. Координаты точки наблюдения в мировой системе координат.

2. Вектор, указывающий направление наблюдения.

3. Плоскость, на которой формируется изображение (плоскость экрана). Эту плоскость можно задать различными способами, например
две пересекающихся прямых, три принадлежащие плоскости неколлинеарные точки, три взаимно перпендикулярных вектора и т. п.

В нашем случае для простоты примем следующее рис. 3.3:

1. Начало мировой системы координат находится в центре объекта.

2. Вектор наблюдения направлен из точки наблюдения Е в начало мировой системы координат.

3. Плоскость экрана перпендикулярна вектору наблюдения, и этот вектор, пересекает ее в центре экрана.

Рис. 3.3. Расположение объектов сцены.

Чтобы получить изображение объекта выполним следующие действия:

1. Повернем мировую систему координат вокруг осей z и y так, чтобы ось х была направлена в точку Е.

2. Перенесем начало этой системы координат в точку Е.

3. Поменяем направление оси х на обратное.

4. Переименуем ось х в z, y в x, z в y.

5. Разместим экран на расстоянии d от точки наблюдения по новой оси z, так, чтобы ось х экрана была параллельна оси х новой системы координат, а ось y экрана – оси y новой системы координат.

Совокупность этих преобразований называется видовым преобразованием, а новая система координат – видовой системой координат.

Если теперь пересчитать координаты вершин объекта в видовой системе координат, и нарисовать на экране сцену используя видовые координаты x и y, игнорируя z, то мы получим изображение параллельной проекции сцены, как она выглядит при наблюдении из точки E.

Рассмотрим, каким образом можно выполнить видовое преобразование.

Будем задавать наше преобразование матрицей 4х4, которая получается путем перемножения следующих 4-х матриц элементарных преобразований:

Матрица поворота системы координат на угол вокруг оси z

рис. 3.4.

Матрица поворота системы координат на угол вокруг оси y.

Матрица переноса начала системы координат в точку Е.

Матрица S преобразования осей системы координат.

Рис. 3.4. Система координат до видового преобразования.

Матрица поворота системы координат вокруг оси z на угол будет следующей:

Как видно из рис. 3: , а, , где

После этого поворота оси координат займут положение как на рис. 3.5.

Рис 3.5. Система координат после поворота вокруг оси z.

Теперь видно, чтобы ось х была направлена в точку Е необходимо повернуть систему координат вокруг оси y на угол . Матрица такого преобразования следующая:

Как видно из рис. 3.5, , а ,
где , а .

Сейчас наша система координат выглядит следующим образом рис. 3.6.

Рис. 3.6. Система координат после поворота вокруг оси y.

Перенесем начало системы координат в точку Е. Матрица для этого преобразования следующая:

, где .

После этого преобразования получим систему координат как на рис. 3.7.

Рис. 3.7. Положение координатных осей после переноса
начала координат в точку Е.

Сейчас необходимо изменить направление оси х на противоположное, и переименовать оси системы координат, для этого воспользуемся следующей матрицей:

Окончательное положение осей видовой системы координат получим следующее рис. 3.8.

Рис. 3.8. Окончательное положение осей видовой системы координат.

Перспективное преобразование.

Если применить полученную матрицу преобразования к координатам вершин объекта, то мы получим координаты вершин объекта в видовой системе координат. Для получения перспективной проекции объекта, мы должны рассчитать новые координаты x и y вершин объекта с учетом их расстояния до точки наблюдения. Эффект перспективы проявляется в кажущемся сокращении расстояний между точками при их движении от наблюдателя рис. 3.9.

Рис. 3.9. Получение перспективной проекции.

Рассмотрим треугольники EPZp и EP'd. Эти треугольники подобны, поэтому . Отсюда .

Таким образом, если точка P задана своими видовыми координатами x, y, z , то координаты x’ и y’ ее центральной проекции на плоскость экрана вычисляются следующим образом:

где d – расстояние от точки наблюдения до экрана.

Последнее, что нам необходимо сделать, это пересчитать полученные координаты проекций точек в системе экранных координат. Экранные координаты Sx и Sy рассчитываются следующим образом:

, где W – ширина экрана, а H его высота.

Задания к лабораторной работе № 3

Перед выдачей заданий, студентов необходимо поделить на пары. Если количество студентов нечетное, то оставшемуся без пары студенту предлагается выполнять вариант №1.

В данной работе необходимо получить на экране компьютера параллельную и перспективную проекции трехмерной сцены. Объектом отображения является трехмерное выпуклое тело, задаваемое в виде каркасной модели, т.е. в виде совокупности координат вершин объекта в трехмерном пространстве, и отрезков прямых линий (ребер), соединяющих эти вершины рис. 3.10.

Рис. 3.10. Каркасная модель куба.

Объекты задаются параметрически, т.е. вы должны в программе рассчитать координаты вершин объекта, и построить списки ребер, для заданных значений основных параметров объекта и его расположения относительно мировой системы координат. Например, объектом является куб, со стороной равной а (конкретное значение задается пользователем). Центр симметрии куба находится в точке О начала системы координат. Ребра куба параллельны соответствующим осям координат. На основе этой информации можно построить объект, показанный на рис. 3.11.

Однако для построения проекции трехмерной сцены, этой информации недостаточно. Как минимум необходимо знать координаты точки наблюдения в мировой системе координат, вектор направления наблюдения, и расположение системы координат экрана компьютера относительно мировой системы координат. Все вышесказанное поясняет рис. 3.12. Здесь нужно отметить, что координаты точки наблюдения задает пользователь.

Рис. 3.11. Параметрически заданный куб.

Рис. 3.12. Получение проекции трехмерной сцены.

Вариант № 1.

Объектом является цилиндр, аппроксимируемый правильной n-гранной призмой рис.3.13. Основания цилиндра параллельны плоскости xy. Нижнее основание лежит в плоскости xy. Центр нижнего основания совпадает с точкой О начала мировой системы координат. Число граней призмы n, радиус описанной вокруг основания окружности r, высота призмы h, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

Рис. 3.13. Цилиндр. Вариант №1.

Вариант № 2.

Объектом является цилиндр, аппроксимируемый правильной n-гранной призмой рис. 3.14. Основания цилиндра параллельны плоскости xy. Нижнее основание лежит в плоскости xy. Центр нижнего основания совпадает с точкой О начала мировой системы координат. Число граней призмы n, длина стороны основания призмы a, высота призмы h, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

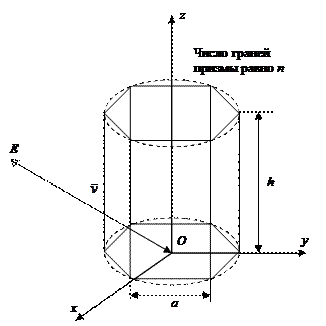
Рис. 3.14. Цилиндр. Вариант №2.

Вариант № 3.

Объектом является конус, аппроксимируемый правильной n-гранной пирамидой рис. 4.15. Основание конуса лежит в плоскости xy. Центр основания совпадает с точкой О начала мировой системы координат. Число граней пирамиды n, радиус описанной вокруг основания окружности r, высота пирамиды h, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

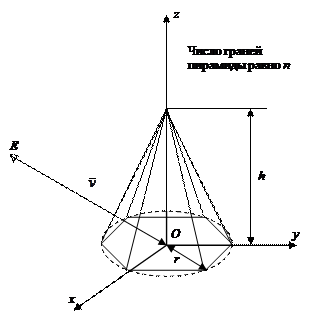
Рис. 3.15. Конус. Вариант №3.

Вариант № 4.

Объектом является конус, аппроксимируемый правильной n-гранной пирамидой рис. 4.16. Основание пирамиды лежит в плоскости xy. Центр основания совпадает с точкой О начала мировой системы координат. Число граней пирамиды n, длина стороны основания пирамиды a, высота пирамиды h, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

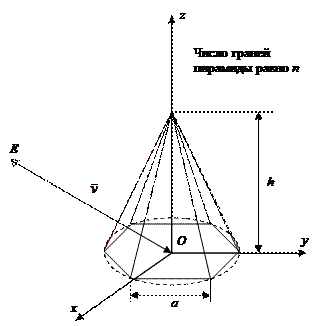
Рис. 3.16. Конус. Вариант №4.

Вариант № 5.

Объектом является конус, аппроксимируемый правильной n-гранной пирамидой рис. 3.17. Основание конуса лежит в плоскости xy. Центр основания совпадает с точкой О начала мировой системы координат. Число граней пирамиды n, радиус описанной вокруг основания окружности r, угол раскрыва конуса β, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

Рис. 3.17. Конус. Вариант №5.

Вариант № 6.

Объектом является конус, аппроксимируемый правильной n-гранной пирамидой рис. 3.18. Основание пирамиды лежит в плоскости xy. Центр основания совпадает с точкой О начала мировой системы координат. Число граней пирамиды n, длина стороны основания пирамиды a, угол раскрыва конуса β, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

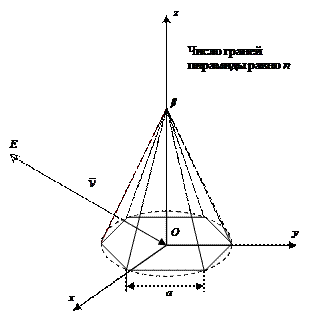
Рис. 3.18. Конус. Вариант №6.

Вариант № 7.

Объектом является сфера, аппроксимируемая многогранником рис. 3.19. Центр сферы совпадает с точкой О начала мировой системы координат. Число параллелей n, число меридианов m, радиус сферы r, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

Рис.3.19. Сфера. Вариант №7.

Вариант № 8.

Объектом является сфера, аппроксимируемая многогранником рис. 3.20. Центр сферы совпадает с точкой О начала мировой системы координат. Число параллелей n, число меридианов m, длина стороны меридиана a, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

Рис. 3.20. Сфера. Вариант №8.

Вариант № 9.

Объектом является полусфера, аппроксимируемая многогранником
рис. 3.21. Основание полусферы лежит в плоскости xy. Центр основания совпадает с точкой О начала мировой системы координат. Число параллелей n, число меридианов m, радиус основания полусферы r, и координаты точки наблюдения E задаются пользователем. Вектор наблюдения направлен в точку О. Необходимо построить параллельную и перспективную проекции данной сцены.

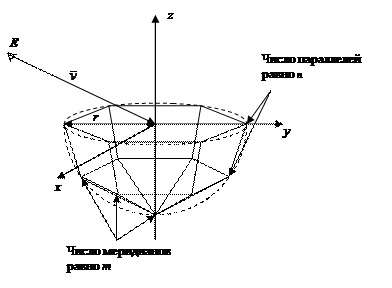
Рис. 3.21. Полусфера. Вариант №9.