
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
М. М. Афанасьева, О.С. Громова, В. А. Павский
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
КЕМЕРОВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ ПИЩЕВОЙ ПРОМЫШЛЕННОСТИ
М. М. Афанасьева, О.С. Громова, В. А. Павский
Учебно-методический комплекс по МАТЕМАТИКе
В 3-х частях
Часть 2
Учебное пособие
Кемерово 2005
УДК:517(075)
Печатается по решению Редакционно-издательского совета Кемеровского технологического института пищевой промышленности
Математика: учебно-методический комплекс, часть 2/ М.М. Афанасьева, О.С. Громова, В.А. Павский Кемеровский технологический институт пищевой промышленности. – Кемерово, 2005г. – 116 с.
Учебно-методический комплекс составлен в соответствии с программой по математике для технических вузов и, хотя предназначен для студентов заочной формы обучения, может быть полезен студентам всех специальностей и всех форм обучения.
Изложение теоретического материала сопровождается рассмотрением большого числа примеров и задач, ведется на доступном, по возможности строгом языке.
Рецензенты:
Кафедра высшей и прикладной математики Кемеровского института МГУК (Заведующий кафедрой, к. ф.-м. н., доцент Астраков С.Н.)
Доцент кафедры ЮНЕСКО по НИТ, к. ф.-м. н. Гудов А.М.

ISB N 5-89289-216-6
© Афанасьева Майя Михайловна
© Громова Ольга Сергеевна
© Павский Валерий Алексеевич
© Кемеровский технологический
институт пищевой промышленности, 2005
Оглавление
введение.. 4
Тема 1. Функции нескольких переменных.. 7
1.1 Общие сведения. 7
1.2 Производные и дифференциалы.. 9
1.3 Экстремумы функции нескольких переменных. 13
1.4 Скалярное поле. Производная по направлению. Градиент. 16
Тема 2. КОМПЛЕКСНЫЕ ЧИСЛА.. 20
тема 3. определенныЙ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛЫ... 26
3.1 Основные понятия и теоремы.. 26
3.2 Методы интегрирования. 36
3.3 Основные классы интегрируемых функций. 43
3.4 Несобственные интегралы.. 51
3.5 Приложения интегрального исчисления к геометрии. 55
ТЕМА 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.. 62
4.1 Основные понятия. 62
4.2 Дифференциальные уравнения 1-го порядка. 63
4.3 Дифференциальные уравнения второго порядка. 72
4.4 Задачи на составление дифференциальных уравнений. 83
ТЕМА 5. РЯДЫ... 85
5.1 Числовые ряды.. 85
5.2 Числовые ряды с положительными членами. 87
5.3 Знакопеременные ряды.. 95
5.4 Степенные ряды.. 99
5.5 Разложение функции в степенной ряд. Ряд Тейлора. 104
5.6 Применение степенных рядов. 108
Контрольные задания.. 110
Введение
Основными задачами преподавания математики студентам нашего вуза являются: а) повышение уровня математической культуры мышления; б) воспитание потребностей использования полученных знаний в других дисциплинах и, в дальнейшем, в своей профессиональной деятельности; в) привитие навыков работы со специальной литературой.
Программа курса математики составлена в объеме, необходимом для изучения фундаментальных, общеинженерных и специальных дисциплин.
Работа студента над учебным материалом состоит из следующих элементов: изучение материала по учебникам и учебным пособиям, выполнение контрольных работ, слушание лекций, участие в практических занятиях, сдача зачета и/или экзамена.
Настоящее пособие включает в себя некоторые теоретические сведения, решение типовых задач и варианты контрольных работ по следующим разделам курса математики: функции нескольких переменных, комплексные числа, интегральное исчисление, дифференциальные уравнения, ряды.
Перед выполнением контрольного задания студент должен изучить соответствующие разделы курса по учебникам или по предлагаемому пособию. После изучения всей темы следует закрепить знания выполнением упражнений. Если студент испытывает затруднения в освоении теоретического или практического материала, то он может обратиться за письменной или устной консультацией на кафедру математики (тел. (3842) 73-42-00, E-mail: [email protected]).
При написании данного пособия была использована следующая литература:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов.- М.: Наука, 1970-2001, т. 1, 2.
2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики.- М.: Наука, 1989.
3. Данко П.Е., Попов А.Г., Кожевников Т.Я. Высшая математика в упражнениях и задачах. - М.: Наука, 1999, ч. 1, 2.
Авторы выражают благодарность всему коллективу кафедры высшей математики КЕМТИПП за помощь в оформлении учебного пособия.
ПРАВИЛА ВЫПОЛНЕНИЯ
И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студенту для переработки.
Каждую контрольную работу следует выполнять в отдельной тетради (файле), чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента. На обложке тетради (титульном листе) должны быть написаны (разборчиво) фамилия студента, его инициалы, учебный номер (шифр), номер контрольной работы, название дисциплины, дата отправки работы в институт и адрес студента. В конце работы следует проставить дату ее выполнения и расписаться.
Количество контрольных работ и заданий в них определяется в зависимости от специальности и в соответствие с учебным планом. В работу должны быть включены все задачи, указанные в задании, соответствующие положенному варианту. Контрольные работы, содержащие не все задачи, а также содержащие задачи не из своего варианта, могут быть не зачтены.
НОМЕР ВАРИАНТА соответствует последней цифре шифра студента в зачетной книжке: шифру 6453 соответствует вариант №3. Решения задач необходимо располагать в порядке номеров, указанных в заданиях, при этом условие задачи должно быть полностью переписано перед ее решением. В том случае, если несколько задач, из которых студент выбирает задачи своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
Решения задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
После получения прорецензированной работы, как не зачтенной, так и зачтенной студент должен исправить все отмеченные рецензентом ошибки и недочеты. Выполнить исправления можно в конце той же тетради (после записи «Работа над ошибками»). В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех дополнений и исправлений. Вносить исправления в сам текст работы после рецензирования запрещается.
Если контрольная работа не зачтена, то ее выполняют еще раз и отправляют на повторную рецензию. При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее.
Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена. Студент не получивший зачета, хотя бы по одной работе, к экзамену (зачету) не допускается.
Общие сведения
В предыдущих разделах рассматривалось совместное изменение двух переменных, одна из которых зависела от другой. В науке нередки случаи, когда для определения значения некоторой величины необходимо установить значения, совместно принимаемые несколькими независимыми переменными.
Так, например, объём  кругового цилиндра есть функция от радиуса
кругового цилиндра есть функция от радиуса 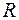 его основания и от высоты
его основания и от высоты  ; зависимость между этими переменными выражается формулой
; зависимость между этими переменными выражается формулой 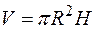 , которая даёт возможность определить значение объёма
, которая даёт возможность определить значение объёма  , зная значения двух переменных
, зная значения двух переменных 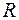 и
и  .
.
Изучая физическое состояние какого-нибудь тела, приходится наблюдать изменение его свойств от точки к точке: температуры, плотности, напряжений и т. д. Все эти величины можно рассматривать как функции координат 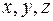 точки, то есть как функции от трёх независимых переменных.
точки, то есть как функции от трёх независимых переменных.
Функции, зависящие от двух и более переменных, называют функциями нескольких переменных.
Наиболее часто приходится иметь дело с функцией от двух переменных. Рассмотрим на плоскости Oxy некоторое множество точек с координатами 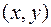 иобозначим его через D.
иобозначим его через D.
ОПРЕДЕЛЕНИЕ. Величину  называют функцией независимых переменных
называют функцией независимых переменных  и
и  на множестве D, если каждой паре
на множестве D, если каждой паре 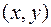 этого множества по некоторому правилу или закону ставится в соответствие одно определенное значение величины
этого множества по некоторому правилу или закону ставится в соответствие одно определенное значение величины  .
.
Множество D называют областью определения функции  .Переменные
.Переменные  и
и  по отношению к функции
по отношению к функции  называют ее аргументами. Функции нескольких переменных могут быть заданы в явном и неявном виде. Функциональная зависимость между
называют ее аргументами. Функции нескольких переменных могут быть заданы в явном и неявном виде. Функциональная зависимость между  и
и  ,
,  обозначается различными способами:
обозначается различными способами: 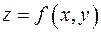 ,
,  ,
, 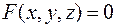 и т.д.
и т.д.
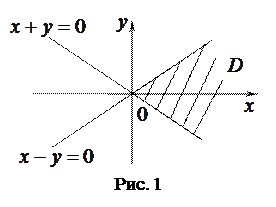 Если пара
Если пара  взята из области
взята из области 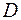 , то
, то 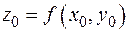 называют частным значением функции
называют частным значением функции 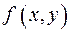 , которое она принимает, когда
, которое она принимает, когда 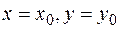 .
.
Пример. Найти область определения функции  . Найти частное значение функции в точке
. Найти частное значение функции в точке 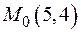 .
.
РЕШЕНИЕ
Квадратный корень определён в случае, если подкоренное выражение является неотрицательным. Поэтому функция  определена при тех действительных значениях переменных
определена при тех действительных значениях переменных  и
и  , для которых одновременно выполняются следующие условия:
, для которых одновременно выполняются следующие условия:  и
и 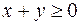 . Геометрическое изображение решения системы неравенств (область определения функции) представлено на рис. 1.
. Геометрическое изображение решения системы неравенств (область определения функции) представлено на рис. 1.
Частное значение функции в точке 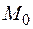 равно
равно 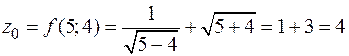 .
.
В общем случае область определения функции двух переменных геометрически может быть представлена некоторым множеством точек (x,у) плоскости.
Подобно тому, как функция  геометрически изображается графиком, можно геометрически задать функцию
геометрически изображается графиком, можно геометрически задать функцию  , ставя в соответствие каждой точке
, ставя в соответствие каждой точке 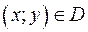 аппликату
аппликату  . Мы получим некоторое множество точек (x; y; z) трехмерного пространства – чаще всего некоторую поверхность. Поэтому равенство
. Мы получим некоторое множество точек (x; y; z) трехмерного пространства – чаще всего некоторую поверхность. Поэтому равенство  называют уравнением поверхности.
называют уравнением поверхности.
 Пример. Пусть задана функция
Пример. Пусть задана функция 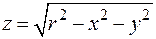 . Ее область определения найдем из неравенства
. Ее область определения найдем из неравенства 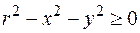 , т.е.
, т.е. 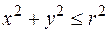 . Это круг с центром в начале координат и радиусом r (рис. 2). Графиком функции
. Это круг с центром в начале координат и радиусом r (рис. 2). Графиком функции 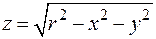 являетсяверхняя половина сферы
являетсяверхняя половина сферы  (разрешив уравнение сферы относительно z, получим две однозначные функции
(разрешив уравнение сферы относительно z, получим две однозначные функции  :
: 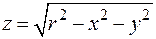 и
и  ).
).
Рассмотрим функцию  и точку
и точку  . Полным приращением функции
. Полным приращением функции  в точке
в точке  называют разность
называют разность 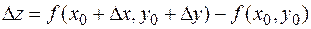 .
.
Если изменение функции  происходит при изменении только одного из аргументов, например х, при фиксированном значении другого аргумента - у, то функция получит приращение
происходит при изменении только одного из аргументов, например х, при фиксированном значении другого аргумента - у, то функция получит приращение
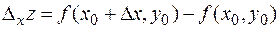 ,
,
которое называют частным приращением функции  по х.
по х.
Также задается частное приращение по переменной  :
: 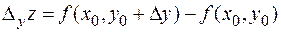 .
.
ОПРЕДЕЛЕНИЕ. Функцию  называют непрерывной в точке
называют непрерывной в точке  , если она определена в некоторой окрестности этой точки и если бесконечно малым приращениям
, если она определена в некоторой окрестности этой точки и если бесконечно малым приращениям  и
и  соответствует бесконечно малое приращение
соответствует бесконечно малое приращение  , т.е.
, т.е.
 , где
, где 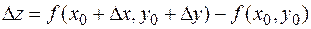 .
.
Обозначим 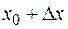 через
через  , а
, а 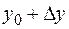 через
через  . Тогда из того, что
. Тогда из того, что  и
и 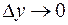 следует, что
следует, что 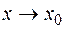 и
и 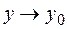 . И условие непрерывности функции
. И условие непрерывности функции  можно записать в виде:
можно записать в виде:
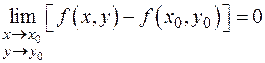 или
или  .
.
Это равенство означает, что функция непрерывна в точке  , если предел функции равен значению функции в предельной точке.
, если предел функции равен значению функции в предельной точке.
Производные и дифференциалы
Рассмотрим функцию 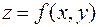 , если изменяется только один из аргументов.
, если изменяется только один из аргументов.
ОПРЕДЕЛЕНИЕ. Частной производной функции 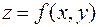 по аргументу
по аргументу  в точке
в точке  называют предел
называют предел
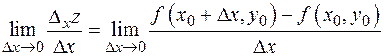
и обозначают одним из символов: 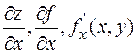 .
.
Аналогично определяется частная производная  по аргументу
по аргументу  :
:
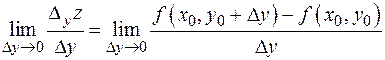 .
.
По определению, каждая частная производная является фактически производной функции одной переменной: 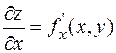 (где у = const),
(где у = const), 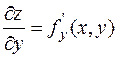 (где
(где  = const). Поэтому при вычислении частных производных можно пользоваться уже известными правилами и формулами дифференцирования функции одной переменной, считая при этом другую переменную фиксированной.
= const). Поэтому при вычислении частных производных можно пользоваться уже известными правилами и формулами дифференцирования функции одной переменной, считая при этом другую переменную фиксированной.
Пример. Найти частные производные функции 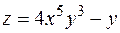 .
.
РЕШЕНИЕ
Имеем
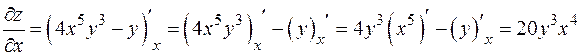
(  фиксировано);
фиксировано);
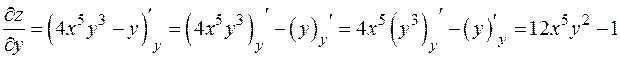
(  фиксировано).
фиксировано).
Пример. Дано 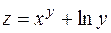 . Найти
. Найти 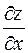 и
и 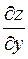 , вычислить их значения в точке А(1; 2).
, вычислить их значения в точке А(1; 2).
РЕШЕНИЕ
Имеем 
(при фиксированном  производная первого слагаемого находится как производная степенной функции, а второго - как производная постоянной);
производная первого слагаемого находится как производная степенной функции, а второго - как производная постоянной);
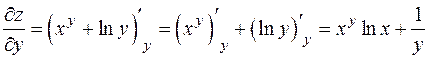
(при фиксированном  производная первого слагаемого находится как производная показательной функции).
производная первого слагаемого находится как производная показательной функции).
Вычислим значения частных производных в точке А(1; 2):
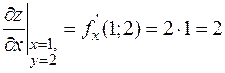 ;
; 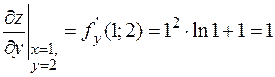 .
.
Аналогично определяются функции трех и более переменных. Если каждому набору значений (x; y; …; t) независимых переменных из множества D соответствует одно определенное значение u из множества E, то u называют функцией переменных x, y, …, t и обозначают u = f(x, y, …, t).
Для функции трех и более переменных геометрической интерпретации не существует.
Частные производные нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.
Пример. Найти частные производные функции 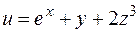 .
.
РЕШЕНИЕ
Имеем  (у и z фиксированы);
(у и z фиксированы); 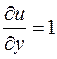 (
(  и
и  фиксированы);
фиксированы); 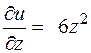 (
(  и y фиксированы).
и y фиксированы).
Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной - это скорость изменения функции относительно изменения одного из аргументов.
Пример.Количественная величина потока П пассажиров железных дорог может быть выражена функцией П = N2/R, где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстояние между пунктами.
Частная производная функции П по R, равная 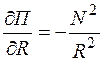 , показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.
, показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.
Частная производная функции П по N, равная 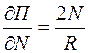 , показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населенных пунктов при одном и том же расстоянии между пунктами.
, показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населенных пунктов при одном и том же расстоянии между пунктами.
ОПРЕДЕЛЕНИЕ. Полным дифференциалом функции 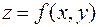 называют главную линейную часть полного приращения функции, линейную относительно приращений независимых переменных.
называют главную линейную часть полного приращения функции, линейную относительно приращений независимых переменных.
Обозначая дифференциал буквой 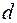 , можно записать
, можно записать  ,
,  ,
,
где  не зависят от
не зависят от  ,
, 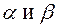 - бесконечно малые при
- бесконечно малые при  .
.
Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемойв этой области.
Сформулируем без доказательства достаточное условие дифференцируемости функции.
ТЕОРЕМА. Если функция  имеет непрерывные частные производные
имеет непрерывные частные производные 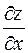 и
и 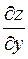 в данной области, то она дифференцируема в этой области и ее дифференциал выражается формулой
в данной области, то она дифференцируема в этой области и ее дифференциал выражается формулой
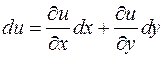
Произведение частной производной на приращение соответствующей независимой переменной называют частным дифференциалом. Частные дифференциалы обозначают:
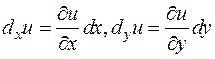 .
.
Сумма частных дифференциалов дает полный дифференциал.
Пример.Найти полный дифференциал функции  .
.
РЕШЕНИЕ
Найдем частные производные функции и запишем полный дифференциал:
 ,
,  ,
,
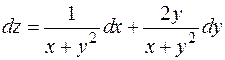 .
.
Так же как и в случае функции одной переменной, из дифференцируемости функции в некоторой области следует ее непрерывность в этой области, но не наоборот.
Частные производные 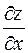 и
и 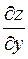 функции f(x, y) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называют частными производными высших порядков. Каждая производная первого порядка имеет две частные производные, которые обозначают так:
функции f(x, y) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называют частными производными высших порядков. Каждая производная первого порядка имеет две частные производные, которые обозначают так:
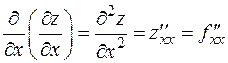 ,
, 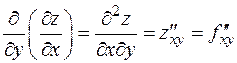 ,
,
 ,
, 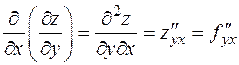 .
.
Производные 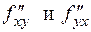 называют смешанными производными.
называют смешанными производными.
Теорема. Если смешанные производные 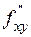 и
и 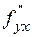 непрерывны в некоторой открытой области, то они равны между собой.
непрерывны в некоторой открытой области, то они равны между собой.
Другими словами, для непрерывной смешанной производной порядок дифференцирования не играет роли.
Пример. Убедиться в равенстве смешанных производных 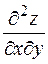 и
и  для функции
для функции  .
.
РЕШЕНИЕ
В любой точке 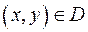 имеем
имеем
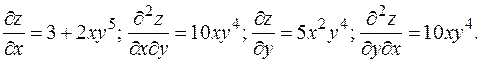
Как и следовало ожидать,  .
.
Частные производные от производных второго порядка называют частными производными третьего порядка и т. д.
Аналогично определяются частные производные высших порядков для функций любого числа независимых переменных.
Тема 2. КОМПЛЕКСНЫЕ ЧИСЛА
Если ограничиваться только вещественными числами, то, действие извлечения корня не всегда выполнимо: корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. Это обстоятельство приводит к необходимости расширения понятия о числе и введению новых чисел с более общими свойствами.
Комплексная плоскость
ОПРЕДЕЛЕНИЕ. Комплексным числом называют выражение вида 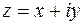 , где
, где  и
и  - действительные числа, а
- действительные числа, а 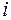 - мнимая единица, удовлетворяющая равенству
- мнимая единица, удовлетворяющая равенству  .
.
Такую форму записи комплексного числа называют алгебраической формой, причем  - вещественной частью, а
- вещественной частью, а  - мнимой частью, что записывается так:
- мнимой частью, что записывается так:  ,
, 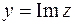 .
.
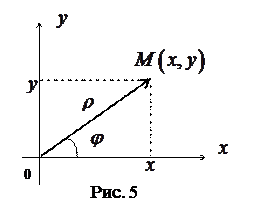 Комплексные числа можно изобразить на плоскости. Для этого выбирают систему декартовых координат
Комплексные числа можно изобразить на плоскости. Для этого выбирают систему декартовых координат  ,
,  , после чего любое комплексное число
, после чего любое комплексное число  отождествляется с радиус-вектором точки
отождествляется с радиус-вектором точки 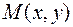 (рис. 5). Такую плоскость называют комплексной плоскостью.
(рис. 5). Такую плоскость называют комплексной плоскостью.
Действительные (вещественные) числа являются частным случаем комплексных чисел, если в формуле 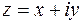 положить
положить  . Они изображаются точками на вещественной оси, т. е. оси
. Они изображаются точками на вещественной оси, т. е. оси 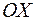 . Если у комплексного числа отсутствует действительная часть
. Если у комплексного числа отсутствует действительная часть  , то его называют чисто мнимым и изображают на мнимой оси, т.е. оси
, то его называют чисто мнимым и изображают на мнимой оси, т.е. оси  .
.
На рис.6 показаны комплексные числа 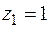 ,
,  и
и 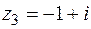 .
.
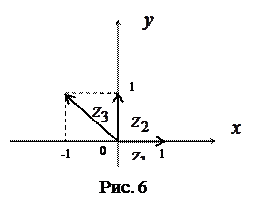
На комплексной плоскости часто рассматривают также полярные координаты 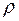 и
и 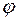 точки
точки 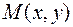 . Их называют модулем и аргументом комплексного числа
. Их называют модулем и аргументом комплексного числа  и обозначают
и обозначают 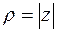 ,
, 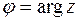 (рис. 5). Связь между модулем и аргументом комплексного числа
(рис. 5). Связь между модулем и аргументом комплексного числа  и его действительной и мнимой частями устанавливается известными формулами:
и его действительной и мнимой частями устанавливается известными формулами:
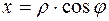 ,
, 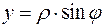 ,
, 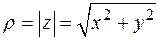 ,
,
 ,
, 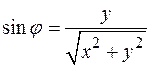 ,
, 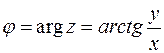 .
.
Заменяя  и
и  в алгебраической форме комплексного числа
в алгебраической форме комплексного числа 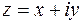 , их выражениями через
, их выражениями через 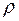 и
и 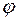 , получим так называемую тригонометрическую форму комплексного числа:
, получим так называемую тригонометрическую форму комплексного числа:
 .
.
Модуль любого комплексного числа имеет вполне определенное значение, тогда как аргумент определен с точностью до целого числа полных оборотов. Поэтому значение полярного угла 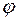 , которое удовлетворяет неравенству
, которое удовлетворяет неравенству  , называется главным значением аргумента
, называется главным значением аргумента 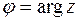 , а функция
, а функция  , где
, где  – общим значениемаргумента.
– общим значениемаргумента.
ПРИМЕР.Найти корни уравнения 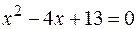 .
.
Решение
Для решения квадратного уравнения с вещественными коэффициентами  воспользуемся известной формулой
воспользуемся известной формулой

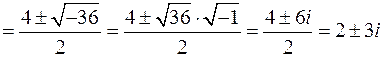 .
.
Уравнение имеет два комплексных корня  и
и  .
.
ПРИМЕР. Записать в тригонометрической форме комплексные числа:
a) 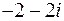 , б)
, б) 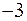 , в)
, в)  .
.
Решение
а) Найдем модуль и аргумент числа 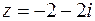 . Так как действительная часть комплексного числа
. Так как действительная часть комплексного числа  , а мнимая часть
, а мнимая часть 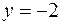 , то
, то
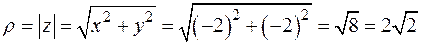 ,
, 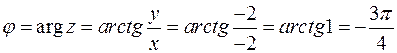 .
.
Для определения угла 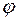 следует помнить, что тангенс угла принимает положительные значения в первой и третьей четвертях. Для определения четверти можно изобразить точку
следует помнить, что тангенс угла принимает положительные значения в первой и третьей четвертях. Для определения четверти можно изобразить точку  , соответствующую числу
, соответствующую числу  на комплексной плоскости, и поскольку она лежит в третьей четверти, то
на комплексной плоскости, и поскольку она лежит в третьей четверти, то  . Отсюда можно записать комплексное число в тригонометрической форме
. Отсюда можно записать комплексное число в тригонометрической форме 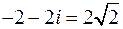
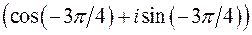 .
.
б) Если 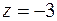 , то
, то 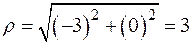 , а
, а  .
.
Отсюда: 
в) Если 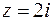 , то
, то 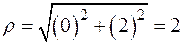 ,
,  .
.
Отсюда:  .
.
Основные понятия и теоремы
Определенный интеграл
Рассмотрим непрерывную на промежутке 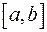 функцию
функцию  .
.  Разобьем отрезок
Разобьем отрезок 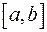 на n частей и составим интегральную сумму:
на n частей и составим интегральную сумму:
 ,
,
где по-прежнему  ,
, 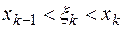 .
.
Найдем предел интегральной суммы, если 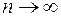 , а
, а 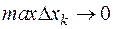
 .
.
ОПРЕДЕЛЕНИЕ. Определенным интегралом функции  в промежутке от
в промежутке от 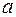 до
до  называется конечный предел, к которому стремится последовательность интегральных сумм, если число разбиений
называется конечный предел, к которому стремится последовательность интегральных сумм, если число разбиений 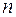 стремится к бесконечности, а длина наибольшего частичного интервала стремится к нулю, и обозначается символом
стремится к бесконечности, а длина наибольшего частичного интервала стремится к нулю, и обозначается символом 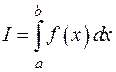 .
.
В случае существования такого предела функция  называется интегрируемой в промежутке
называется интегрируемой в промежутке 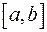 .
.
Знак интеграла 
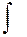 - стилизованная буква S (сумма),
- стилизованная буква S (сумма), 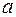 и
и  – граничные точки области интегрирования – называют соответственно нижним и верхнимпределами интегрирования,
– граничные точки области интегрирования – называют соответственно нижним и верхнимпределами интегрирования,  – подынтегральная функция,
– подынтегральная функция, 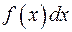 – подынтегральное выражение. При постоянных пределах интегрирования определенный интеграл представляет собой постоянное число.
– подынтегральное выражение. При постоянных пределах интегрирования определенный интеграл представляет собой постоянное число.
Применяя определение интеграла к задаче о вычислении площади криволинейной трапеции, можно записать, что

 , если
, если 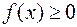 .
.
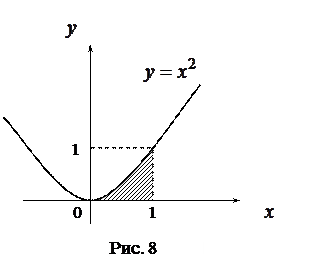
ПРИМЕР. Вычислить площадь фигуры, ограниченной линиями 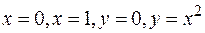 (рис.8).
(рис.8).
РЕШЕНИЕ
 I этап.
I этап.
1. Разобьем промежуток интегрирования 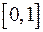 на 5 равных частей.
на 5 равных частей.
2. Для простоты выберем точки 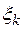 в левом конце отрезков:
в левом конце отрезков:
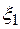 = 0,0;
= 0,0; 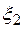 =0,2;
=0,2;  =0,4;
=0,4;  =0,6;
=0,6;  =0,8.
=0,8.
3. Значения функции в точке 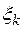 будут равны
будут равны  .
.
4. Построим интегральную сумму
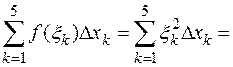
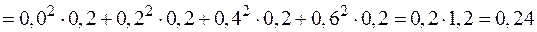 .
.
Получим, что 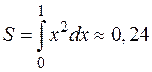 .
.
II этап.Разобьем интервал интегрирования на 10 частей и аналогично, выбрав точки 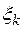 ,
,  , получим, что
, получим, что 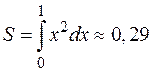 .
.
III этап.Если разобьем интервал на 100 частей, то  .
.
В дальнейшем покажем, что точное значение площади равно 1/3. В данном примере уже после третьего разбиения видно, что S→ 1/3, но решение задачи было трудоемким. Поэтому необходимо использовать более простые приемы.
Неопределенный интеграл
ОПРЕДЕЛЕНИЕ. Функцию F(x), производная которой равна подынтегральной функции, называют первообразной.
Как нахождение производной было одной из основных задач дифференциального исчисления, так нахождение первообразной является одной из основных задач интегрального исчисления.
Например, рассмотрим функцию 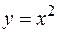 . Мы знаем, что
. Мы знаем, что 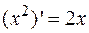 . Функция
. Функция 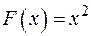 первообразная для функции
первообразная для функции  .
.
Если найти производные от функций 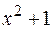 ,
, 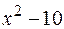 ,
,  , где
, где  - произвольная постоянная величина, то все они равны
- произвольная постоянная величина, то все они равны  . Следовательно, любая из функций
. Следовательно, любая из функций  является первообразной для функции
является первообразной для функции  .
.
ТЕОРЕМА 2. Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым.
ДОКАЗАТЕЛЬСТВО.
Предположим, что функция  имеет первообразную функцию
имеет первообразную функцию  . Тогда функция
. Тогда функция 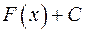 при всякой постоянной
при всякой постоянной  будет также первообразной, так как
будет также первообразной, так как  . Итак, функция
. Итак, функция  имеет бесчисленное множество первообразных.
имеет бесчисленное множество первообразных.
Пусть функции
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...