
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Тема 1. Функции нескольких переменных
Общие сведения
В предыдущих разделах рассматривалось совместное изменение двух переменных, одна из которых зависела от другой. В науке нередки случаи, когда для определения значения некоторой величины необходимо установить значения, совместно принимаемые несколькими независимыми переменными.
Так, например, объём  кругового цилиндра есть функция от радиуса
кругового цилиндра есть функция от радиуса 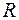 его основания и от высоты
его основания и от высоты  ; зависимость между этими переменными выражается формулой
; зависимость между этими переменными выражается формулой 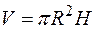 , которая даёт возможность определить значение объёма
, которая даёт возможность определить значение объёма  , зная значения двух переменных
, зная значения двух переменных 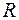 и
и  .
.
Изучая физическое состояние какого-нибудь тела, приходится наблюдать изменение его свойств от точки к точке: температуры, плотности, напряжений и т. д. Все эти величины можно рассматривать как функции координат 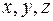 точки, то есть как функции от трёх независимых переменных.
точки, то есть как функции от трёх независимых переменных.
Функции, зависящие от двух и более переменных, называют функциями нескольких переменных.
Наиболее часто приходится иметь дело с функцией от двух переменных. Рассмотрим на плоскости Oxy некоторое множество точек с координатами 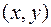 иобозначим его через D.
иобозначим его через D.
ОПРЕДЕЛЕНИЕ. Величину  называют функцией независимых переменных
называют функцией независимых переменных  и
и  на множестве D, если каждой паре
на множестве D, если каждой паре 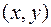 этого множества по некоторому правилу или закону ставится в соответствие одно определенное значение величины
этого множества по некоторому правилу или закону ставится в соответствие одно определенное значение величины  .
.
Множество D называют областью определения функции  .Переменные
.Переменные  и
и  по отношению к функции
по отношению к функции  называют ее аргументами. Функции нескольких переменных могут быть заданы в явном и неявном виде. Функциональная зависимость между
называют ее аргументами. Функции нескольких переменных могут быть заданы в явном и неявном виде. Функциональная зависимость между  и
и  ,
,  обозначается различными способами:
обозначается различными способами: 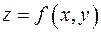 ,
,  ,
, 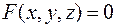 и т.д.
и т.д.
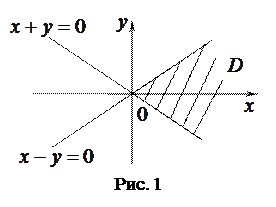 Если пара
Если пара  взята из области
взята из области 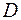 , то
, то 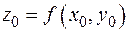 называют частным значением функции
называют частным значением функции 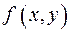 , которое она принимает, когда
, которое она принимает, когда 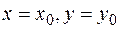 .
.
Пример. Найти область определения функции  . Найти частное значение функции в точке
. Найти частное значение функции в точке 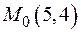 .
.
РЕШЕНИЕ
Квадратный корень определён в случае, если подкоренное выражение является неотрицательным. Поэтому функция  определена при тех действительных значениях переменных
определена при тех действительных значениях переменных  и
и  , для которых одновременно выполняются следующие условия:
, для которых одновременно выполняются следующие условия:  и
и 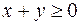 . Геометрическое изображение решения системы неравенств (область определения функции) представлено на рис. 1.
. Геометрическое изображение решения системы неравенств (область определения функции) представлено на рис. 1.
Частное значение функции в точке 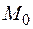 равно
равно 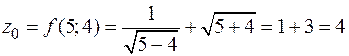 .
.
В общем случае область определения функции двух переменных геометрически может быть представлена некоторым множеством точек (x,у) плоскости.
Подобно тому, как функция  геометрически изображается графиком, можно геометрически задать функцию
геометрически изображается графиком, можно геометрически задать функцию  , ставя в соответствие каждой точке
, ставя в соответствие каждой точке 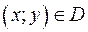 аппликату
аппликату  . Мы получим некоторое множество точек (x; y; z) трехмерного пространства – чаще всего некоторую поверхность. Поэтому равенство
. Мы получим некоторое множество точек (x; y; z) трехмерного пространства – чаще всего некоторую поверхность. Поэтому равенство  называют уравнением поверхности.
называют уравнением поверхности.
 Пример. Пусть задана функция
Пример. Пусть задана функция 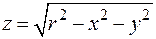 . Ее область определения найдем из неравенства
. Ее область определения найдем из неравенства 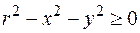 , т.е.
, т.е. 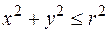 . Это круг с центром в начале координат и радиусом r (рис. 2). Графиком функции
. Это круг с центром в начале координат и радиусом r (рис. 2). Графиком функции 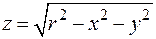 являетсяверхняя половина сферы
являетсяверхняя половина сферы  (разрешив уравнение сферы относительно z, получим две однозначные функции
(разрешив уравнение сферы относительно z, получим две однозначные функции  :
: 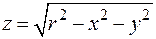 и
и  ).
).
Рассмотрим функцию  и точку
и точку  . Полным приращением функции
. Полным приращением функции  в точке
в точке 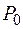 называют разность
называют разность 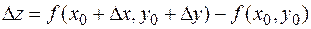 .
.
Если изменение функции  происходит при изменении только одного из аргументов, например х, при фиксированном значении другого аргумента - у, то функция получит приращение
происходит при изменении только одного из аргументов, например х, при фиксированном значении другого аргумента - у, то функция получит приращение
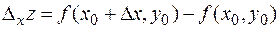 ,
,
которое называют частным приращением функции  по х.
по х.
Также задается частное приращение по переменной  :
: 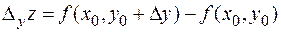 .
.
ОПРЕДЕЛЕНИЕ. Функцию  называют непрерывной в точке
называют непрерывной в точке  , если она определена в некоторой окрестности этой точки и если бесконечно малым приращениям
, если она определена в некоторой окрестности этой точки и если бесконечно малым приращениям  и
и  соответствует бесконечно малое приращение
соответствует бесконечно малое приращение  , т.е.
, т.е.
 , где
, где 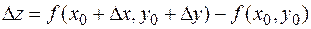 .
.
Обозначим 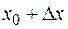 через
через  , а
, а 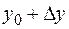 через
через  . Тогда из того, что
. Тогда из того, что  и
и 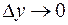 следует, что
следует, что 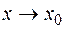 и
и 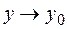 . И условие непрерывности функции
. И условие непрерывности функции  можно записать в виде:
можно записать в виде:
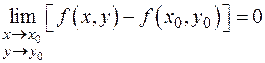 или
или  .
.
Это равенство означает, что функция непрерывна в точке  , если предел функции равен значению функции в предельной точке.
, если предел функции равен значению функции в предельной точке.
Производные и дифференциалы
Рассмотрим функцию 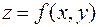 , если изменяется только один из аргументов.
, если изменяется только один из аргументов.
ОПРЕДЕЛЕНИЕ. Частной производной функции 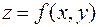 по аргументу
по аргументу  в точке
в точке  называют предел
называют предел
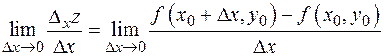
и обозначают одним из символов: 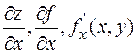 .
.
Аналогично определяется частная производная  по аргументу
по аргументу  :
:
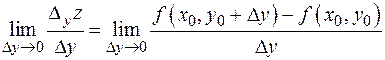 .
.
По определению, каждая частная производная является фактически производной функции одной переменной: 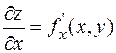 (где у = const),
(где у = const), 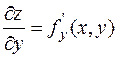 (где
(где  = const). Поэтому при вычислении частных производных можно пользоваться уже известными правилами и формулами дифференцирования функции одной переменной, считая при этом другую переменную фиксированной.
= const). Поэтому при вычислении частных производных можно пользоваться уже известными правилами и формулами дифференцирования функции одной переменной, считая при этом другую переменную фиксированной.
Пример. Найти частные производные функции 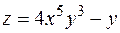 .
.
РЕШЕНИЕ
Имеем
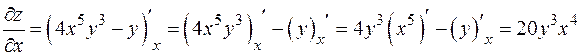
(  фиксировано);
фиксировано);
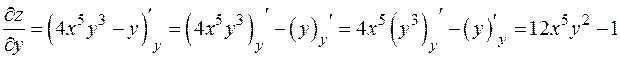
(  фиксировано).
фиксировано).
Пример. Дано 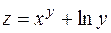 . Найти
. Найти 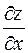 и
и 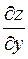 , вычислить их значения в точке А(1; 2).
, вычислить их значения в точке А(1; 2).
РЕШЕНИЕ
Имеем 
(при фиксированном  производная первого слагаемого находится как производная степенной функции, а второго - как производная постоянной);
производная первого слагаемого находится как производная степенной функции, а второго - как производная постоянной);
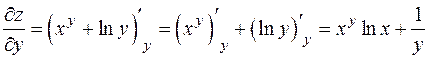
(при фиксированном  производная первого слагаемого находится как производная показательной функции).
производная первого слагаемого находится как производная показательной функции).
Вычислим значения частных производных в точке А(1; 2):
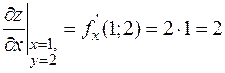 ;
; 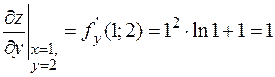 .
.
Аналогично определяются функции трех и более переменных. Если каждому набору значений (x; y; …; t) независимых переменных из множества D соответствует одно определенное значение u из множества E, то u называют функцией переменных x, y, …, t и обозначают u = f(x, y, …, t).
Для функции трех и более переменных геометрической интерпретации не существует.
Частные производные нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.
Пример. Найти частные производные функции 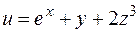 .
.
РЕШЕНИЕ
Имеем  (у и z фиксированы);
(у и z фиксированы); 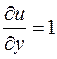 (
(  и
и  фиксированы);
фиксированы); 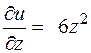 (
(  и y фиксированы).
и y фиксированы).
Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной - это скорость изменения функции относительно изменения одного из аргументов.
Пример.Количественная величина потока П пассажиров железных дорог может быть выражена функцией П = N2/R, где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстояние между пунктами.
Частная производная функции П по R, равная 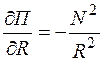 , показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.
, показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.
Частная производная функции П по N, равная 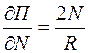 , показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населенных пунктов при одном и том же расстоянии между пунктами.
, показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населенных пунктов при одном и том же расстоянии между пунктами.
ОПРЕДЕЛЕНИЕ. Полным дифференциалом функции 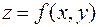 называют главную линейную часть полного приращения функции, линейную относительно приращений независимых переменных.
называют главную линейную часть полного приращения функции, линейную относительно приращений независимых переменных.
Обозначая дифференциал буквой 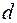 , можно записать
, можно записать  ,
,  ,
,
где  не зависят от
не зависят от  ,
, 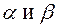 - бесконечно малые при
- бесконечно малые при  .
.
Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемойв этой области.
Сформулируем без доказательства достаточное условие дифференцируемости функции.
ТЕОРЕМА. Если функция  имеет непрерывные частные производные
имеет непрерывные частные производные 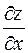 и
и 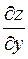 в данной области, то она дифференцируема в этой области и ее дифференциал выражается формулой
в данной области, то она дифференцируема в этой области и ее дифференциал выражается формулой
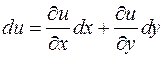
Произведение частной производной на приращение соответствующей независимой переменной называют частным дифференциалом. Частные дифференциалы обозначают:
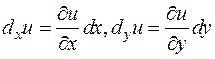 .
.
Сумма частных дифференциалов дает полный дифференциал.
Пример.Найти полный дифференциал функции  .
.
РЕШЕНИЕ
Найдем частные производные функции и запишем полный дифференциал:
 ,
,  ,
,
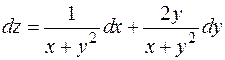 .
.
Так же как и в случае функции одной переменной, из дифференцируемости функции в некоторой области следует ее непрерывность в этой области, но не наоборот.
Частные производные 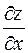 и
и 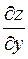 функции f(x, y) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называют частными производными высших порядков. Каждая производная первого порядка имеет две частные производные, которые обозначают так:
функции f(x, y) сами являются некоторыми функциями тех же переменных и, в свою очередь, могут иметь производные по разным переменным, которые называют частными производными высших порядков. Каждая производная первого порядка имеет две частные производные, которые обозначают так:
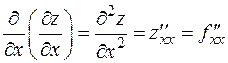 ,
, 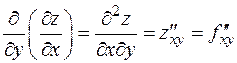 ,
,
 ,
, 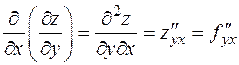 .
.
Производные 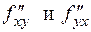 называют смешанными производными.
называют смешанными производными.
Теорема. Если смешанные производные 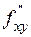 и
и 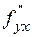 непрерывны в некоторой открытой области, то они равны между собой.
непрерывны в некоторой открытой области, то они равны между собой.
Другими словами, для непрерывной смешанной производной порядок дифференцирования не играет роли.
Пример. Убедиться в равенстве смешанных производных 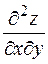 и
и  для функции
для функции  .
.
РЕШЕНИЕ
В любой точке 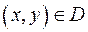 имеем
имеем
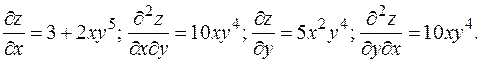
Как и следовало ожидать,  .
.
Частные производные от производных второго порядка называют частными производными третьего порядка и т. д.
Аналогично определяются частные производные высших порядков для функций любого числа независимых переменных.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...