Числовые ряды с положительными членами

Числовой ряд называют рядом с положительными членами, если все его члены неотрицательны, т.е. если

Практически редко возникает необходимость в вычислении суммы ряда, а достаточно знать, сходится ряд или расходится. Установить это можно с помощью достаточных признаков сходимости.

Интегральный признак Коши

Пусть - числовой ряд с положительными членами, и пусть - непрерывная, монотонно убывающая функция, для которой . Тогда ряд сходится, если сходится несобственный интеграл , и расходится, если этот интеграл расходится.

ДОКАЗАТЕЛЬСТВО

Составим частичную сумму ряда . Поскольку ( ), то .

Каждое слагаемое частичной суммы можно рассматривать как площадь прямоугольника с основанием единица и высотой равной (рис.25). Добавление к частичной сумме нового члена ряда означает добавление новой площади, а потому , то есть последовательность частичных сумм неубывающая.

Рассмотрим частичную сумму и примем за площадь прямоугольника, лежащего справа от , т. е. с большей высотой. Тогда получим сумму площадей прямоугольников, часть площади которых расположена над кривой . Эта сумма равна .

Обозначим . С геометрической точки зрения этот интеграл есть площадь, ограниченная кривой при и осью .

Тогда из рис. 25 имеем, что

.

Это двойное неравенство можно записать в виде двух неравенств:

и .

1). Пусть сходится. Это значит, что существует конечный предел . Тогда согласно первому неравенству , где 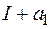- число. Следовательно, возрастающая последовательность ограниченна сверху, а потому имеет конечный предел, т. е. ряд сходится.

2). Пусть расходится. Тогда

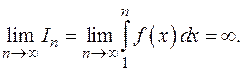
Согласно неравенству , частичные суммы неограниченно возрастают. Но тогда, по определению, ряд расходится.

ПРИМЕР. Исследовать на сходимость обобщенный гармонический ряд .

РЕШЕНИЕ

Если , то члены ряда составляют монотонно убывающую последовательность .

Рассмотрим функцию непрерывную на промежутке , монотонно убывающую и при целых значениях аргумента, совпадающую с членами ряда.

Вычислим , если :

Если , то .

Таким образом, ряд сходится, если и расходится если .

ПРИМЕР. Исследовать на сходимость ряд .

РЕШЕНИЕ

Общий член ряда . Вычислим интеграл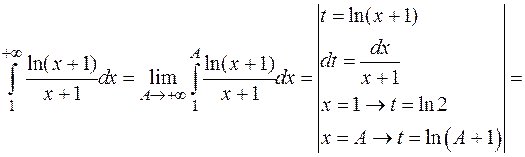

.

Т.к. предел равен бесконечности, интеграл расходится. Следовательно, по интегральному признаку Коши, исследуемый ряд тоже расходится.

Рассмотрим два ряда с положительными членами:

и

Первый признак сравнения

Если, начиная с некоторого номера, выполняется неравенство: , то из сходимости ряда (2) вытекает сходимость ряда (1), или из расходимости ряда (1) следует расходимость ряда (2).

ДОКАЗАТЕЛЬСТВО

На основании того, что отбрасывание конечного числа начальных членов ряда не изменяет его поведение, можно считать, что 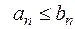при всех значениях 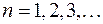. Обозначим через - частичную сумму ряда (1), а через 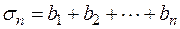- частичную сумму ряда (2). Будем иметь: .

1). Пусть ряд 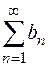сходится , тогда его частичные суммы ограничены суммой ряда . В силу предыдущего неравенства

.

Т.к. все члены ряда (1) неотрицательны, то последовательность его частичных сумм является монотонно возрастающей и ограниченной сверху . Известно, что такая последовательность имеет конечный предел 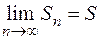. Это означает, что ряд (1) сходится.

2). Пусть ряд расходится. Тогда его частичные суммы неограниченно возрастают, т.е. . Мы показали, что поэтому и . Ряд (2) также расходится.

Для решения примеров удобнее применять второй признак сравнения.

Второй признак сравнения

Если существует конечный отличный от нуля предел 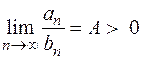(если ), то оба ряда сходятся или оба расходятся одновременно.

ДОКАЗАТЕЛЬСТВО

Пусть ряд (2) сходится и . Взяв произвольное число , для достаточно больших номеров 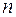будем иметь или . Из неравенства следует, что . В силу свойств сходящихся рядов одновременно с рядом (2) будет сходиться и ряд , полученный умножением его членов на число .Отсюда, по первому признаку сравнения, вытекает сходимость ряда (1).

Если же ряд (2) расходится, то из неравенства или следует, что ряд (1) также расходится.

Трудность применения на практике признаков сравнения состоит в необходимости иметь “запас” рядов, сходимость (или расходимость) которых известна. В качестве «эталонных» рядов, обычно используются ряды, образованные членами геометрической прогрессии, или обобщенный гармонический ряд .

ПРИМЕР. Исследовать на сходимость числовой ряд .

РЕШЕНИЕ

Сравним данный ряд с рядом

.

Ряд сходится, т.к. его члены образуют бесконечно убывающую геометрическую прогрессию со знаменателем . Каждый член исследуемого ряда меньше соответствующего члена ряда :

поэтому, согласно первому признаку сравнения, ряд сходится.

ПРИМЕР. Исследовать на сходимость ряд

Признак Даламбера

Пусть для числового ряда с положительными членами , существует предел ,

то при l<1 ряд сходится, при l>1 ряд расходится, при l=1 вопрос о сходимости ряда остается нерешенным (надо применить другой признак).

ДОКАЗАТЕЛЬСТВО

По определению предела для любого существует , что для любого выполняется соотношение

или .

1). Пусть . Выберем так, чтобы число . Тогда, если , и т. д. Отсюда получим, что , , ,....

Ряд сходится, так как члены ряда образуют геометрическую прогрессию со знаменателем . Тогда по первому признаку сравнения ряд

также сходится. Этот ряд получен из ряда после отбрасывания первых членов (остаток ряда). Значит, ряд сходится (свойство 3).

2). Пусть . Тогда, начиная с некоторого номера, будет выполняться неравенство (если выбрать достаточно малым).

Из этого неравенства следует, что каждый последующий член ряда будет больше предыдущего , а т.к. они положительны, то предел общего члена ряда не может быть равен нулю. Следовательно, в силу необходимого признака сходимости, ряд расходится.

3). Пусть l=1. Возьмем два известных ряда: .

В том и другом случае 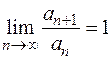, но при этом один ряд сходится, а другой расходится. Поэтому в случае, когда этот предел равен 1, необходимо применять другой признак для решения вопроса о сходимости ряда.

ПРИМЕР. Исследовать на сходимость ряд числовой .

РЕШЕНИЕ

Общий член этого ряда имеет вид .

Для того чтобы найти й член ряда , вместо n в выражение подставим n+1: .

Вычислим предел

.

Т.к. , а то после сокращения получим

.

По признаку Даламбера, если то ряд сходится.

ПРИМЕР. Исследовать на сходимость числовой ряд .

РЕШЕНИЕ.

Общий член ряда . Запишем последующий член ряда . Найдем предел отношения

.

Т.к. то по признаку Даламбера ряд расходится.

Знакопеременные ряды