
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Знакочередующиеся ряды. Признак Лейбница
ОПРЕДЕЛЕНИЕ. Знакочередующимся рядом называют числовой ряд, члены которого имеют чередующиеся знаки.
Если первый член ряда положительный, то знакочередующийся ряд можно записать в виде:
 , где
, где 
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости.
Признак Лейбница
Если члены знакочередующегося ряда  монотонно убывают по абсолютной величине, т. е.
монотонно убывают по абсолютной величине, т. е. 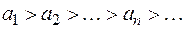 и общий член ряда стремится к нулю
и общий член ряда стремится к нулю 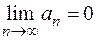 , то
, то
1) ряд сходится;
2) его сумма не превосходит абсолютной величины первого члена ряда;
Модуль суммы остатка ряда не превосходит абсолютной величины первого отброшенного члена.
ДОКАЗАТЕЛЬСТВО
Построим последовательность частичных сумм знакочередующегося ряда  с четными индексами:
с четными индексами:

Поскольку любая скобка в этой сумме положительна, то последовательность  возрастающая. Докажем, что она ограничена. Для этого представим
возрастающая. Докажем, что она ограничена. Для этого представим  в виде:
в виде:
 .
.
Здесь также каждая из скобок положительна. Поэтому в результате вычитания из  положительных чисел получаем число, меньше чем
положительных чисел получаем число, меньше чем  , т.е.
, т.е.  для любого
для любого 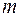 .
.
Итак, последовательность  - возрастающая, ограниченная сверху, значит, она имеет конечный предел. Обозначим его через S, т.е.
- возрастающая, ограниченная сверху, значит, она имеет конечный предел. Обозначим его через S, т.е. 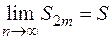 , причем
, причем  .
.
Теперь рассмотрим последовательность частичных сумм ряда с нечетными индексами:
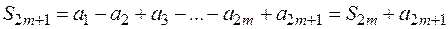 .
.
Согласно условию  , поэтому
, поэтому

Таким образом, предел частичных сумм равен S как для сумм с четными индексами, так и для сумм с нечетными индексами.
Следовательно, 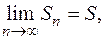 а это значит, что ряд сходится и его сумма равна S.
а это значит, что ряд сходится и его сумма равна S.
Рассмотрим остаток ряда: 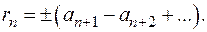 Он также является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница. Следовательно, он сходится и его сумма
Он также является знакочередующимся рядом, удовлетворяющим условиям признака Лейбница. Следовательно, он сходится и его сумма  меньше абсолютной величины первого члена
меньше абсолютной величины первого члена  т.е.
т.е. 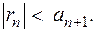
ПРИМЕР. Пользуясь признаком Лейбница исследовать на сходимость ряд

РЕШЕНИЕ. Выпишем члены ряда :  и применим признак Лейбница. Проверим выполнение условий этого признака:
и применим признак Лейбница. Проверим выполнение условий этого признака:
Легко убедится, что с возрастанием n, члены ряда убывают по абсолютной величине  и
и  . Таким образом, исследуемый ряд сходится.
. Таким образом, исследуемый ряд сходится.
Знакопеременные ряды. Абсолютная и условная сходимость
ОПРЕДЕЛЕНИЕ. Ряд 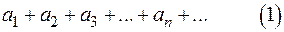 называют знакопеременным, если среди его членов есть как положительные, так и отрицательные числа.
называют знакопеременным, если среди его членов есть как положительные, так и отрицательные числа.
Достаточный признак сходимости
Если ряд  , составленный из абсолютных величин знакопеременного ряда, сходится, то ряд (1) тоже сходится.
, составленный из абсолютных величин знакопеременного ряда, сходится, то ряд (1) тоже сходится.
ДОКАЗАТЕЛЬСТВО
Обозначим через  - частичную сумму ряда (1). Выберем из этих слагаемых положительные члены и их сумму обозначим
- частичную сумму ряда (1). Выберем из этих слагаемых положительные члены и их сумму обозначим  . Сумму оставшихся отрицательных членов, взятых по абсолютной величине, обозначим
. Сумму оставшихся отрицательных членов, взятых по абсолютной величине, обозначим  . Тогда
. Тогда  .
.
Частичную сумму ряда (2) обозначим  . По условию ряд (2) сходится, значит,
. По условию ряд (2) сходится, значит,  имеет конечный предел
имеет конечный предел  , (
, (  ) причем
) причем  .
.
Так как можно записать  то
то  и
и  . Таким образом
. Таким образом  - возрастающие и ограниченные последовательности и, следовательно, они имеют предел, если
- возрастающие и ограниченные последовательности и, следовательно, они имеют предел, если 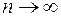 . Тогда последовательность
. Тогда последовательность  тоже имеет предел, а это значит, что ряд (1) сходится.
тоже имеет предел, а это значит, что ряд (1) сходится.
ОПРЕДЕЛЕНИЕ. Знакопеременный ряд называют абсолютно сходящимся, если ряд, составленный из абсолютных величин этого ряда, сходится.
Сходящийся знакопеременный ряд называют условно сходящимся, если ряд, составленный из абсолютных величин его членов, расходится.
ЗАМЕЧАНИЕ. Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.
Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов, причем сумма ряда не зависит от порядка следования его членов.
Если ряд сходится условно, то можно так переставить члены этого ряда, что сумма ряда изменится. Более того, можно так переставить члены ряда, что ряд, полученный после перестановки, окажется расходящимся.
ПРИМЕР. Исследовать на сходимость ряд  .
.
РЕШЕНИЕ
Этот ряд знакопеременный, т.к. 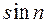 при различных значениях n может быть как положительным, так и отрицательным.
при различных значениях n может быть как положительным, так и отрицательным.
Составим ряд из абсолютных величин членов ряда:

и применим к нему первый признак сравнения.
Так как при любом n  то для каждого слагаемого можно записать оценку:
то для каждого слагаемого можно записать оценку:  .
.
Таким образом, члены ряда из абсолютных величин не превосходят соответствующие члены сходящегося ряда  . Согласно первому признаку сравнения ряд, составленный из абсолютных величин, сходится. Из этого следует сходимость ряда с произвольными членами, т. е. ряд сходится абсолютно.
. Согласно первому признаку сравнения ряд, составленный из абсолютных величин, сходится. Из этого следует сходимость ряда с произвольными членами, т. е. ряд сходится абсолютно.
ПРИМЕР. Исследовать на сходимость ряд  .
.
РЕШЕНИЕ
Запишем ряд в виде 
Составим ряд из абсолютных величин членов ряда (1):

Это числовой ряд с положительными членами, общий член которого имеет вид  . Обобщенный гармонический ряд
. Обобщенный гармонический ряд  расходится.
расходится.
Таким образом, исследуемый ряд (1) не может быть абсолютно сходящимся. Проверим его на условную сходимость.
Так как ряд (1) знакочередующийся, то к нему применим признак Лейбница. Проверим два условия:
 - члены ряда по модулю убывают,
- члены ряда по модулю убывают,  .
.
Следовательно, ряд (1) сходится условно.
Степенные ряды
ОПРЕДЕЛЕНИЕ. Функциональным рядом называют выражение
 ,
,
члены которого  являются функциями от x, определенными на некотором множестве X.
являются функциями от x, определенными на некотором множестве X.
Если задать переменной  числовое значение
числовое значение  , то получится числовой ряд
, то получится числовой ряд  ,
,
который может быть как сходящимся, так и расходящимся.
ОПРЕДЕЛЕНИЕ. Множество значений  , при которых функциональный ряд сходится, называется его областью сходимости.
, при которых функциональный ряд сходится, называется его областью сходимости.
В области сходимости сумма функционального ряда является некоторой функцией от переменной  и определяется как
и определяется как
 .
.
Например, ряд 
сходится, если 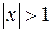 (члены ряда образуют геометрическую прогрессию со знаменателем
(члены ряда образуют геометрическую прогрессию со знаменателем  ), и расходится, если
), и расходится, если  .
.
Областью сходимости ряда служат два промежутка 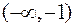 и
и  .
.
Одним из видов функциональных рядов являются степенные ряды, которые записывают:
 ,
,
где  - последовательность действительных чисел, коэффициенты ряда;
- последовательность действительных чисел, коэффициенты ряда;  - центр области сходимости ряда.
- центр области сходимости ряда.
Если  степенной ряд принимает вид:
степенной ряд принимает вид:
 .
.
Рассмотрим свойства степенных рядов на примере ряда (*), т.к. любой степенной ряд общего вида легко преобразовать к виду (*) подстановкой  .
.
Теорема Абеля
Если степенной ряд  сходится в точке
сходится в точке  , то он сходится абсолютно в интервале
, то он сходится абсолютно в интервале  , т.е. при всех x, удовлетворяющих условию
, т.е. при всех x, удовлетворяющих условию  .
.
ДОКАЗАТЕЛЬСТВО
По условию теоремы в точке  степенной ряд
степенной ряд  сходится. Общий членсходящегосячислового ряда
сходится. Общий членсходящегосячислового ряда  , в силу необходимого признака, стремится к нулю:
, в силу необходимого признака, стремится к нулю: 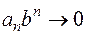 , поэтому все члены ряда ограничены некоторым числом
, поэтому все члены ряда ограничены некоторым числом  :
:  . То есть
. То есть
 .
.
Представим степенной ряд  в виде
в виде

и составим ряд из абсолютных величин его членов:
 .
.
Сравним его с рядом, составленным из членов геометрической прогрессии:  . Этот ряд сходится, если
. Этот ряд сходится, если  и знаменатель прогрессии
и знаменатель прогрессии 
В силу неравенств  , члены ряда
, члены ряда  меньше соответствующих членов сходящегося ряда
меньше соответствующих членов сходящегося ряда  , по первому признаку сравнения, ряд
, по первому признаку сравнения, ряд  также сходится.
также сходится.
Мы показали, что при любом  из интервала
из интервала  степенной ряд
степенной ряд  сходится, значит, ряд
сходится, значит, ряд  внутри этого интервала сходится абсолютно.
внутри этого интервала сходится абсолютно.
Следствие. Если степенной ряд  расходится в точке
расходится в точке  , то он расходится при любом x, по модулю, большем, чем b, т.е. если
, то он расходится при любом x, по модулю, большем, чем b, т.е. если 
Таким образом, можно сказать, что для любого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число R, что для всех x, по модулю меньших R (  ), ряд сходится абсолютно, а для всех x, по модулю больших R(
), ряд сходится абсолютно, а для всех x, по модулю больших R(  ), ряд расходится.
), ряд расходится.
ОПРЕДЕЛЕНИЕ. Радиусом сходимости степенного ряда  называют такое число R, что для всех
называют такое число R, что для всех  ,
,  , степенной ряд сходится, а для всех
, степенной ряд сходится, а для всех  ,
,  , расходится. Интервал
, расходится. Интервал  называют интервалом сходимости степенного ряда.
называют интервалом сходимости степенного ряда.
Замечание. Для степенного ряда  областью сходимости служит интервал
областью сходимости служит интервал 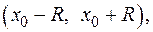 симметричный относительно точки
симметричный относительно точки  .
.
На границах интервала сходимости, в точках  степенной ряд
степенной ряд  может вести себя различным образом.
может вести себя различным образом.
ПРИМЕР. Найти интервал и область сходимости степенного ряда
 .
.
РЕШЕНИЕ
Рассмотрим ряд, составленный из абсолютных величин 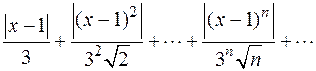 .
.
Все члены этого ряда положительны, поэтому к нему можно применить признак Даламбера: 
 ,
,

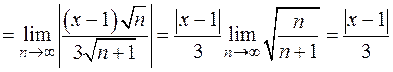 .
.
Найдем значения  , при которых этот предел будет меньше единицы, т.е. решим неравенство
, при которых этот предел будет меньше единицы, т.е. решим неравенство  . Умножим обе части неравенства на 3:
. Умножим обе части неравенства на 3: 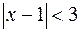 и запишем полученное неравенство в виде двойного неравенства:
и запишем полученное неравенство в виде двойного неравенства:  . Интервал симметричен относительно точки
. Интервал симметричен относительно точки  , а радиус сходимости
, а радиус сходимости 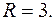
Исследуем сходимость ряда на концах интервала. В точке  получим ряд с положительными членами
получим ряд с положительными членами
 .
.
Это обобщенный гармонический ряд, который, как мы знаем, расходится (  ).
).
В точке  получим знакочередующийся ряд
получим знакочередующийся ряд
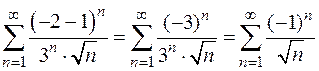 .
.
Его сходимость обсуждалась выше, было доказано что ряд сходится условно.
Окончательно, областью сходимости степенного ряда является промежуток  , причем, если
, причем, если  ряд сходится условно. Радиус сходимости степенного ряда равен
ряд сходится условно. Радиус сходимости степенного ряда равен 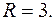
ПРИМЕР. Найти интервал сходимости ряда  .
.
РЕШЕНИЕ
Общий член ряда имеет вид  , тогда
, тогда  .
.
Составим ряд из абсолютных величин и применим к нему признак Даламбера:  .
.
После сокращения на множители  и
и  и вынесения за знак предела множителя
и вынесения за знак предела множителя  , не зависящего от n, выражение примет вид:
, не зависящего от n, выражение примет вид:
 .
.
Таким образом, предел равен нулю при любом x, т.е. по признаку Даламбера областью сходимости этого ряда является вся числовая ось.
Свойства степенных рядов
Для степенных рядов справедливы следующие утверждения:
1). Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.
2). Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны  , где
, где 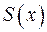 - сумма ряда.
- сумма ряда.
3). Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до  , если
, если  , причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд.
, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...