
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Системы массового обслуживания (СМО)
7.1. Основные определения
Многие экономические задачи связаны с системами массового обслуживания (СМО), то есть такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнения каких – либо услуг, а с другой – происходит удовлетворение этих запросов. СМО включают в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающее устройство (канал обслуживания), выходящий поток требований.
Любая СМО характеризуется следующими параметрами:
1. n – количество обслуживающих каналов;
2. m – количество обслуживаемых объектов (число поступающих в систему требований);
3. λ – интенсивность потока требований (среднее число требований, поступающих в систему за единицу времени);
4. 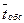 - среднее время обслуживания одного требования;
- среднее время обслуживания одного требования;
5.  - количество требований, обслуживаемых за единицу времени;
- количество требований, обслуживаемых за единицу времени;
6.  - показатель загрузки системы, характеризующий математическое ожидание числа требований, поступающих в систему за время, равное
- показатель загрузки системы, характеризующий математическое ожидание числа требований, поступающих в систему за время, равное 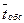 .
.
Рассмотрим СМО с ожиданием (очередью). В этом случае требования, поступившие в момент, кода все обслуживающие каналы заняты, становятся в очередь и обслуживаются по мере освобождения каналов обслуживания. Очевидно, что в этом случае число поступающих в систему требований больше числа каналов обслуживания,
 .
.
Введем основные характеристики СМО с ожиданием.
1) Вероятность 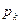 того, системой обслуживается ровно k требований. Отдельно рассматриваются случаи:
того, системой обслуживается ровно k требований. Отдельно рассматриваются случаи:
а)  - вероятность того, что все обслуживающие каналы свободны;
- вероятность того, что все обслуживающие каналы свободны;
б) 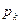 ,
,  , количество требований не превосходит числа каналов обслуживания;
, количество требований не превосходит числа каналов обслуживания;
в) 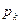 ,
,  , количество требований больше числа каналов обслуживания.
, количество требований больше числа каналов обслуживания.
2) Средняя длина очереди  , то есть среднее число требований, ожидающих начала обслуживания.
, то есть среднее число требований, ожидающих начала обслуживания.
3) Коэффициент простоя обслуживаемого требования:
 .
.
4) Среднее число  свободных обслуживающих каналов.
свободных обслуживающих каналов.
5) Коэффициент простоя обслуживающих каналов:
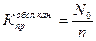 .
.
6) Среднее число занятых каналов
 .
.
7) Коэффициент загрузки обслуживающих каналов:
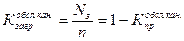 .
.
Замкнутые СМО с ожиданием
К замкнутым относятся СМО, в которых поступающий поток требований ограничен. В подобных системах циркулирующий поток требований ограничен и, как правило, постоянен.
Приведем основные расчетные формулы:
 ;
;
 ;
;
 ;
;
также рассчитывается среднее число М требований, находящихся в системе, обслуживаемых и ожидающих начала обслуживания:
 ;
;
 .
.
Пример 7.1. Рабочий обслуживает группу из трех станков. Поток поступающих требований имеет интенсивность λ = 2. Обслуживание одного станка у рабочего занимает в среднем 12 минут. Необходимо провести анализ рассматриваемой СМО.
Имеем:
n = 1, m = 3.
Временные параметры выразим в часах:
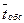 = 12 минут или
= 12 минут или 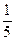 часа,
часа,
следовательно
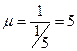 .
.
Параметр
 .
.
Вероятность 

 .
.
Найденную вероятность можно интерпретировать так: рабочий будет свободен 28,22% всего рабочего времени.
Средняя длина очереди равна 
 ; величина
; величина 
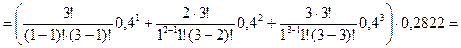
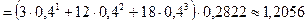 .
.
Итак, в среднем 0,4876 станка ожидают начала обслуживания, а 1,2056 станка простаивает (не выдает продукции).
Коэффициент простоя обслуживающих каналов равен
 .
.
Получаем: в среднем станки простаивают 16,25% своего рабочего времени, ожидая начала обслуживания.
Величина  ,
,
 ;
;
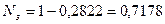 ,
,
 .
.
Разомкнутые СМО с очередями
Если источник обладает бесконечным числом требований, то системы называются разомкнутыми. Для таких СМО поступающий поток требований можно считать неограниченным.
Введем условие:

Это означает, что среднее число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступающие требования. Другими словами, очередь не может расти бесконечно.
Основные показатели функционирования системы рассчитываются по формулам:
 ;
;
 ;
;
вероятность того, что все обслуживающие каналы заняты –
 ;
;
среднее время ожидания начала обслуживания –
 ;
;
 ;
;
 .
.
Пример 7.2. Ателье по ремонту радиоаппаратуры имеет 5 мастеров. В среднем от населения поступает в течение рабочего дня 10 радиоаппаратов. Каждый мастер успевает починить за рабочий день в среднем 2,5 радиоаппарата. Требуется оценить работу ателье.
Имеем:
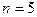 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Вероятность  того, что все мастера свободны от ремонта, равна:
того, что все мастера свободны от ремонта, равна:
 .
.
Вероятность π того, что все мастера заняты работой, равна:
 .
.
Найдем среднее время обслуживания каждого радиоаппарата в ателье. Поскольку все исходные данные имеет единицу измерения «рабочий день», то при переводе их в «часы» учитываем 8 часовой рабочий день. Поэтому
 (часа).
(часа).
Каждый радиоаппарат находится без ремонта в ателье в среднем
 (часа).
(часа).
В среднем в ателье ожидает начала ремонта
 (аппарата).
(аппарата).
Определим среднее число мастеров, свободных от работы:

 (мастера).
(мастера).
Таким образом, в течение рабочего дня свободным от работы оказывается в среднем
 или 19 %
или 19 %
персонала ателье. Соответственно, число занятых работой мастеров равно
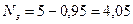 (мастера),
(мастера),
что составляет
 (%)
(%)
численности мастеров в ателье.
Межотраслевой баланс
Постановка задачи
Имеется n отраслей промышленности, производящей некоторую продукцию. Условимся эту продукцию выражать в денежном эквиваленте. Часть произведенной продукции идет на внутрипроизводственное потребление (непосредственное потребление). Другая часть продукции направляется на конечное потребление, то есть вне сферы внутрипроизводственного потребления. Пусть известны прямые затраты, то есть затраты отрасли i , i = 1, 2,…, n, на производство единицы продукции отраслью j, j = 1, 2,…, n.
Основной задачей межотраслевого баланса является ответ на вопрос: чему должен быть валовой выпуск продукции каждой из отраслей , чтобы при заданных прямых затратах обеспечить определенное значение конечного продукта. Наряду с валовой и конечной продукцией рассматривается чистая продукция – разность между валовой продукцией отрасли и продукции всех отраслей, пошедших на ее производство.
Модель Леонтьева
Обозначим 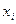 и
и  - соответственно валовая и конечная продукция отрасли i,
- соответственно валовая и конечная продукция отрасли i, 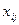 - часть продукции отрасли i, идущая на потребление отраслью j. Очевидно, что
- часть продукции отрасли i, идущая на потребление отраслью j. Очевидно, что
 ,i = 1, 2,…, n.
,i = 1, 2,…, n.
Коэффициент
 ,j = 1, 2,…, n, (8.1)
,j = 1, 2,…, n, (8.1)
определяющий долю продукции отрасли i, идущую на производство единицы продукции отраслью j, называется коэффициентом прямых затрат. Для относительно небольшого промежутка времени коэффициент прямых затрат можно считать зависящим только от технологии производства, поэтому  можно считать постоянным числом.
можно считать постоянным числом.
Пусть  - матрица – столбец валового выпуска,
- матрица – столбец валового выпуска,  - матрица – столбец конечного продукта,
- матрица – столбец конечного продукта,
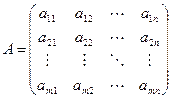 (8.2)
(8.2)
- матрица прямых затрат. Тогда  можно найти с помощью следующего матричного произведения:
можно найти с помощью следующего матричного произведения:
 , (8.3)
, (8.3)
при этом
 (8.4)
(8.4)
есть матрица полных затрат,  - единичная матрица порядка n. Произведение (8.3) называется моделью Леонтьева.
- единичная матрица порядка n. Произведение (8.3) называется моделью Леонтьева.
Модель Леонтьева считается продуктивной, если в матрице А (8.2)
1) максимум сумм ее элементов  по каждому столбцу j не больше единицы,
по каждому столбцу j не больше единицы,
 ,
,
 , i = 1, 2,…, n, j = 1, 2,…, n,
, i = 1, 2,…, n, j = 1, 2,…, n,
2) хотя бы для одного столбца
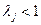 .
.
Чистая продукция  каждой из отраслей равна:
каждой из отраслей равна:
 .
.
Схема решения.
1. Составляем баланс за отчетный период:
| Производящие отрасли | Потребляющие отрасли | Непосредственное потребление | Конечное потребление | Валовой выпуск | |||

| 
| … | 
| ||||

| 
| 
| … | 
| 
| 
| 
|

| 
| 
| … | 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| … | 
| 
| 
| 
|
2. Определяем коэффициенты прямых затрат по формуле (8.1), составляем матрицу А прямых затрат, матрицу 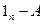 . Эти вычисления удобно производить в таблице:
. Эти вычисления удобно производить в таблице:
| А | 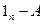
| ||||||

| 
| … | 
| 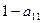
| 
| … | 
|

| 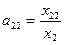
| … | 
| 
| 
| … | 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| … | 
| 
| 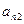
| … | 
|

| 
| … | 
| - | - | - | - |
3. используя определение и последнюю строку предыдущей таблицы, определяем продуктивность модели.
4. Находим матрицу полных затрат.
5. Вычисляем планируемое конечное потребление:
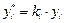 .
.
6. С помощью модели Леонтьева (8.3) определяем валовой выпуск продукции  отраслей.
отраслей.
7. Находим чистую продукцию каждой из отраслей.
8. Составляем новый баланс:
| Производящие отрасли | Потребляющие отрасли | Непосредственное потребление | Конечное потребление | Валовой выпуск | Чистая продукция | |||

| 
| … | 
| |||||

| 
| 
| … | 
| 
| 
| 
| 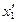
|

| 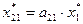
| 
| … | 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| … | 
| 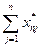
| 
| 
| 
|
Пример 8.1. Имеются данные об исполнении баланса за отчетный период:
| Производящие отрасли | Потребляющие отрасли | Конечное потребление | ||
| А | В | С | ||
| А | ||||
| В | ||||
| С |
Составить межотраслевой баланс, если конечный продукт у отрасли А увеличится на 20%, у отрасли В этот показатель останется на прежнем уровне, а у отрасли С – сократится на 10%.
Найдя валовой выпуск и непосредственное потребление каждой из отраслей, записываем данные в исходной таблице:
| Производящие отрасли | Потребляющие отрасли | Непосредственное потребление | Конечное потребление | Валовой выпуск | ||
| А | В | С | ||||
| А | ||||||
| В | ||||||
| С |
Теперь, находим коэффициенты прямых затрат, устанавливаем коэффициенты прямых затрат, устанавливаем вид матриц А и 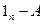 :
:
| А | 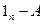
| ||||
| 0,07 | 0,14 | 0,20 | 0,93 | -0,14 | -0,20 |
| 0,09 | 0,10 | 0,10 | -0,09 | 0,90 | -0,10 |
| 0,12 | 0,02 | 0,08 | -0,12 | -0,02 | 0,92 |
| 0,28 | 0,26 | 0,38 | - | - | - |
Переходим к нахождению матрицы полных затрат (8.4), то есть матрицы, обратной к
 .
.
Ее определитель 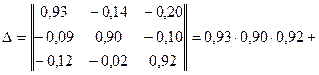

 .
.
Алгебраические дополнения равны:
 ;
;
 ;
;
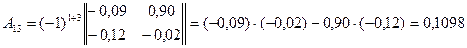 ;
;
 ;
;
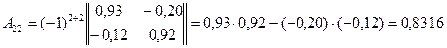 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Получаем:
 .
.
Определяем величину конечного продукта. Исходя из условий задачи
 .
.
Следовательно, валовой выпуск равен
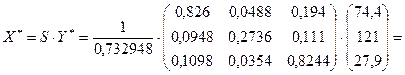
 .
.
Это означает, что валовой выпуск отрасли А необходимо увеличить до 113,1537 (д. е.), для отрасли В – до 151,1344 (д. е.), а валовой выпуск отрасли С должен быть сокращен до 48,3708 (д. е.).
Чистая продукция каждой из отраслей равна
 (д. е.);
(д. е.);
 (д. е.);
(д. е.);
 (д. е.).
(д. е.).
Составляем новый баланс:
| Производящие отрасли | Потребляющие отрасли | Непосредственное потребление | Конечное потребление | Валовой выпуск | Чистая продукция | ||
| А | В | С | |||||
| А | 7,9208 | 21,1588 | 9,6742 | 38,7537 | 74,4 | 113,1537 | 81,4707 |
| В | 10,1838 | 15,1134 | 4,8371 | 30,1344 | 151,1344 | 111,8395 | |
| С | 13,5784 | 3,0227 | 3,8697 | 20,4708 | 27,9 | 48,3708 | 28,9899 |
9. Сетевое планирование
На практике часто возникает необходимость планирования, взаимной увязки и согласования сложного комплекса работ. Например, при разработке плана строительства торгового центра, проведении капитального ремонта и т. д. Разработать оптимальный план, оценить сроки его реализации, выявить наиболее напряженные работы, определить напряженные участки работ, оптимально распределить трудовые и материальные ресурсы, позволяет сетевое планирование.
Рассмотрим основные этапы решения сетевой задачи на примере.
Пример 9.1. Разработать план развития торговой сети. Исходные данные приведены в таблице:
| Работа | Содержание работы | Длительность работы (дни) |
| I | Изучение материалов анализа сети за отчетный период | |
| II | Изучение соответствия торговой сети объему и структуре товарооборота | |
| III | Изучение степени обеспеченности населения торговой сетью | |
| IV | Расчет показателей эффективности использования торговой сети | |
| V | Анализ технического оснащения торговых предприятий | |
| VI | Определение нормативов торговой площади на 1000 жителей | |
| VII | Анализ типов розничных предприятий | |
| VIII | Расчет общей потребности в торговой сети | |
| IX | Определение возможного ввода и выбытия торговой площади | |
| X | Определение площади нового строительства |
1. Исходя из взаимосвязанности работ и строгой последовательности их выполнения, каждую работу будем обозначать в виде пары чисел (событий) (i,j), i>j, а время ее исполнения обозначим  . Тогда исходные данные представляются следующим образом:
. Тогда исходные данные представляются следующим образом:
| Работа | I | II | III | IV | V | VI | VII | VIII | IX | X |
| (i,j) | (1,2) | (2,3) | (3,4) | (3,5) | (3,8) | (4,8) | (5,6) | (5,7) | (6,7) | (7,8) |

|
2. Начальное событие 1 и конечное событие 8 соединяются различными последовательностями работ:
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
3. Для каждой из найденных последовательностей суммарную продолжительность всех работ:
 ;
;
 (дней);
(дней);
 (дня);
(дня);
 (дня);
(дня);
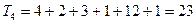 (дня).
(дня).
4. Путь, соединяющий первое и последнее события, и имеющий максимальную продолжительность времени, называется критическим. Величина критического пути определяет минимальное время, за которое может быть реализован весь комплекс работ. В нашем случае критическим путем является вторая последовательность,
 .
.
5. Полученные последовательности работ представляем в виде сетевого графика. На нем каждая работа представлена следующим образом (рисунок 13):

Рис. 13
События, лежащие на критическом пути, обозначим двойным кружком, а стрелки, их соединяющие – также двойные. Итак, сетевой график для рассматриваемой задачи имеет вид (рисунок 14):

Рис. 14
6. Ранний срок  события j рассчитывается по формуле:
события j рассчитывается по формуле:
 .
.
Всегда ранний срок первого события равен нулю, а ранний срок последнего события равен величине критического пути. Для рассматриваемого примера получаем:
 ;
;
 ;
;
 ;
;
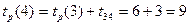 ;
;
 ;
;
 ;
;
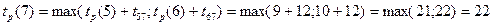 ;
;
 .
.
Поскольку  , то расчеты произведены верно.
, то расчеты произведены верно.
7. Поздний срок  события i равен:
события i равен:
 .
.
Расчет поздник сроков начинается с последнего события. Его поздний срок принимается равным величине  . В качестве контроля правильности произведенных вычислений, пользуемся свойством: поздний срок начального события равен нулю. Получаем:
. В качестве контроля правильности произведенных вычислений, пользуемся свойством: поздний срок начального события равен нулю. Получаем:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
8. По каждой работе необходимо определить резервы времени, то есть определенные задержки во времени исполнения, которые не сказываются на сроках выполнения всего комплекса работ. Определим следующие резервы времени исполнения работы (i,j):
1) полный резерв  ;
;
2) гарантийный резерв  ;
;
3) свободный резерв  ;
;
4) независимый резерв  .
.
Свободные и независимые резервы могут оказаться отрицательными числами. Тогда их полагают равными нулю.
Необходимыми и достаточными условиями принадлежности работы критическому пути являются: 1) ранние и поздние сроки для них совпадают и 2) все резервы времени равны нулю.
9. Результаты вычислений собираем в таблице:
| Работы, (i,j) | Дли-
тель-ность
рабо-
ты,

| Начало работы | Окончание работы | Резервы времени | ||||||

| 
| 
| 
| 
| 
| 
| 
| |||
| I | (1,2) | |||||||||
| II | (2,3) | |||||||||
| III | (3,4) | |||||||||
| IV | (3,5) | |||||||||
| V | (3,8) | |||||||||
| VI | (4,8) | |||||||||
| VII | (5,6) | |||||||||
| VIII | (5,7) | |||||||||
| IX | (6,7) | |||||||||
| X | (7,8) |
Полученная таблица позволяет получить полную информацию о каждой запланированной работе. В качестве примера, проанализируем строку VI таблицы. На определение нормативов торговой площади на 1000 жителей было запланировано 6 дней. Она должна начаться самое раннее через 9 дней после начала всего комплекса работ, а самое позднее – через 18 дней. Данная работа должна завершиться день в день – через 24 дня после начала реализации плана. Резервы времени соответственно равны: полный и свободный – по 9 дней, гарантийного и независимого резервов времени нет.
10. Строим диаграмму, позволяющую наглядно представить график выполнения работ по дням (рисунок 15).

 |
Рис. 15
II. ТИПОВОЙ РАСЧЕТ
Типовой расчет является обязательным для выполнения студентами всех специальностей и любой формы обучения. Его вариант определяется порядковым номером фамилии студента в экзаменационной ведомости.
Типовой расчет необходимо выполнить в ученической тетради в клетку (12 или 18 листов) ручкой любого цвета, кроме красного. Требуется соблюдать последовательность выполнения задач. Перед решением задачи нужно записать ее условие. При необходимости, ход решения задачи снабжается комментариями и ссылками на соответствующие положения, теоремы. Текст типового расчета завершается списком использованной литературы.
Типовой расчет № 4
(100 вариантов, M – первая цифра, N- вторая цифра номера варианта)
Задача №1. Предприятие для производства двух изделий (А и В) использует сырье трех типов. Известно, что для производства одного изделия А требуется сырье 1- го типа в количестве  (ед.), 2 - го типа -
(ед.), 2 - го типа -  (ед.) и 3 – го типа -
(ед.) и 3 – го типа -  (ед.), а для производства изделия В -
(ед.), а для производства изделия В -  ,
,  и
и  соответственно. Запасы сырья на предприятии ограничены и составляют величины
соответственно. Запасы сырья на предприятии ограничены и составляют величины  ,
,  и
и  соответственно. Известно также, что прибыль от реализации одного изделия А составляет р (руб.), а одного изделия В – q (руб.). Требуется составить такой план производства изделий из имеющегося сырья, чтобы суммарная прибыль от реализации всех изделий была максимальной (для этого построить соответствующую математическую модель и решить полученную задачу линейного программирования графически и симплекс методом). Получить двойственные оценки ресурсов и дать их экономический анализ.
соответственно. Известно также, что прибыль от реализации одного изделия А составляет р (руб.), а одного изделия В – q (руб.). Требуется составить такой план производства изделий из имеющегося сырья, чтобы суммарная прибыль от реализации всех изделий была максимальной (для этого построить соответствующую математическую модель и решить полученную задачу линейного программирования графически и симплекс методом). Получить двойственные оценки ресурсов и дать их экономический анализ.
| M | ||||||||||
| р | ||||||||||
| q | ||||||||||
| N | ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

| ||||||||||

|
Задача №2. Торговым предприятием разработаны две хозяйственные стратегии  и
и  с учетом возможных вариантов поведения покупателей на основе изучения покупательского спроса
с учетом возможных вариантов поведения покупателей на основе изучения покупательского спроса  ,
,  и
и  . Платежная матрица представляет собой оценки прибыли (тыс. руб.) торгового предприятия:
. Платежная матрица представляет собой оценки прибыли (тыс. руб.) торгового предприятия:
 .
.
| M | ||||||||||

| ||||||||||

| -1 | -1 | ||||||||
| |
||||||||||
|
Последнее изменение этой страницы: 2016-07-23 lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда... |