Краткая история начертательной геометрии

УЧЕБНОЕ ПОСОБИЕ

по курсу «Начертательная геометрия»

МОДУЛЬ №1

Тольятти 2007

УДК 514.18(076)

ББК 22.15.3

Н36

Рецензент:

к.т.н., доцент А.Г. Егоров (ТГУ).

Н36Начертательная геометрия. Модуль №1: учеб.-метод. Пособие / сост. Т.А. Варенцова, Г.Н. Уполовникова. – Тольятти : ТГУ, 2007.- 40 с.

Содержит полный теоретический материал для успешного освоения студентами курса «Начертательная геометрия». Учебный материал разбит на 4 модуля. Каждый модуль является логически завершенной частью, заканчивается контрольными вопросами и тестом с ответами для самоконтроля студента.

Для студентов технических специальностей высших учебных заведений

Рекомендовано к изданию методической комиссией автомеханического института Тольяттинского государственного университета

© Т.А. Варенцова, Г.Н. Уполовникова,

Составление, 2007

© Тольяттинский государственный

Университет, 2007

Содержание

Введение. 4

Предмет и метод курса. 4

Символика и обозначения. 4

Примеры символической записи. 5

Цель и задачи курса. 5

Краткая история начертательной геометрии. 5

Методы проецирования. Основные свойства проецирования. Комплексный чертеж точки, прямой линии, кривой линии. 6

Методы проецирования. 7

Аппарат проецирования. 8

Центральное проецирование. 9

Параллельное проецирование. 10

Свойства параллельных проекций. 10

Ортогональное проецирование. Свойства ортогонального проецирования. 12

Метод Монжа. 14

Доказательство обратимости чертежа Монжа. 18

Трёхкартинный комплексный чертёж точки. 19

Связь ортогональных проекций точки с её прямоугольными координатами. 21

Контрольные вопросы.. 23

Тест № 1. 24

Комплексный чертеж линии. 24

Задание прямой на комплексном чертеже. 25

Прямые общего положения. 25

Прямые уровня. 26

Горизонталь. 27

Фронталь. 27

Профильная прямая. 27

Проецирующие прямые. 28

Фронтально проецирующая прямая. 29

Профильно проецирующая прямая. 29

Контрольные вопросы.. 30

Тест №2. 30

Взаимное положение прямых на комплексном чертеже. 30

Пресекающиеся прямые. 31

Параллельные прямые. 31

Скрещивающиеся прямые. 31

Контрольные вопросы.. 33

Тест №3. 33

Справочный материал. 33

Комплексный чертеж кривых линий. 34

Метод хорд. 35

Касательная, нормаль к кривой. 36

Особые точки кривых линий. 37

Свойства проекций кривых линий. 38

Некоторые плоские кривые линии. 39

Эллипс. 39

Парабола. 40

Гипербола. 41

Эвольвента. 42

Комплексный чертеж пространственной кривой. Цилиндрическая винтовая линия. 43

Ответы на тесты - № 1, 2, 3. 44

Тест № 1. 44

Тест № 2. 44

Тест № 3. 44

Примеры положения точки и прямой относительно плоскостей проекций. 44

Задание прямых на комплексном чертеже. 47

Введение

Как вы думаете?

1) В начертательной геометрии при изучении метода проецирования рассматривается не геометрическая фигура, а ее проекции («тень») на соответствующие плоскости проекций. А где же, в таком случае, находится сам предмет?

2) Каким это образом по трем искаженным (в общем случае) проекциям геометрической фигуры (а тень очень редко соответствует своему оригиналу) можно определить его конфигурацию и положение в пространстве?

3) Почему, проецируя предмет на три взаимно перпендикулярные плоскости проекций, которые пересекаются по осям x, y, z, в начертательной геометрии чаще пользуются безосными чертежами?

4) В начертательной геометрии утверждается, что предмет проецируется, в общем случае, на плоскости проекций с искажением. Тогда почему "искаженные проекции" облегчает процесс выполнения и чтения чертежа?

Ответить на эти вопросы Вы сможете, изучив курс Начертательной геометрии.

Предмет и метод курса

Данный курс рассчитан на студентов инженерно - технических специальностей ТГУ и соответствует государственной программе курса начертательной геометрии. Начертательная геометрия является фундаментальной дисциплиной развития научно - технической базы каждой страны.

Начертательная геометрия изучает пространственные формы и их отношения, используя метод проецирования («начертания»), с помощью которого строятся различные изображения, в том числе и технические чертежи. В теории изображения изучаются законы построения отображений различных фигур на плоскости. На основе этих законов выполняются чертежи как сложнейших машин и механизмов, так и простых деталей и моделей, а также формируется возможность изображать и такие предметы, которые существуют лишь в воображении человека.

Чертеж имеет исключительно большое значение в практической деятельности человека. Он является средством выражения замысла ученого, конструктора и основным производственным документом, по которому осуществляется строительство зданий и инженерных сооружений, создание машин, механизмов и их составных частей. Начертательная геометрия является основой графической грамотности и позволяет просто и наглядно решать графическими методами многие важные теоретические и практические задачи. В настоящем учебном пособии изложен краткий курс начертательной геометрии, базирующийся на положениях высшей геометрии, которая имеет многочисленные разделы (например, элементарная, аналитическая, проективная).

Символика и обозначения

1. Точки - прописными буквами латинского алфавита(А,В,С) или арабскими цифрами(1,2,3).
2. Линии - строчными буквами латинского алфавита (a, b, c...)
3. Поверхности - прописными буквами греческого алфавита: Г - гамма, D - дельта, L - лямбда, S - сигма, Ф - фи, Y - пси, W - омега...
4. Углы - Ð АВС, а ^Ù b, m ^Ù АВ или a, b, g...
5. Параллельность - ||
6. Перпендикулярность - ^
7. Касание - È
8. Совпадение или тождество - =
9. Принадлежность, включение - Ì или Î, концы знака направлены в сторону большемерной фигуры.
10. Пересечение - Ç
11. Вращение - ã
12. Логическое следствие - Þ
13. Фигура, проецирующая относительно... - ^^.
14. Скрещивающиеся прямые - °
15. Расстояние между элементами пространства - | | : | АВ | - расстояние от точки А до точки В; | Аа | - расстояние от точки А до линии а; | ab | - расстояние между линиями а и b; | АS | - расстояние от точки А до поверхности S; | ГS | - расстояние между поверхностями.

Примеры символической записи

1. S(а Ç b) || Г(А,m) - плоскость, заданная пересекающимися прямыми а и b, параллельна плоскости, заданной точкой А и прямой m
2. АВ ^ Г - отрезок АВ перпендикулярен плоскости Г.
3. А₁ =В₁ - проекции точек А и В совпадают.
4. А Î а - точка А принадлежит прямой а.
5. а Ì S - прямая а принадлежит плоскости S.
6. А Î b - прямая b проходит через точку А.
7. S È Ф(ОА) - плоскость S, касательная к сфере Ф, заданной центром О и точкой А, принадлежащей сфере.

Цель и задачи курса

Цель курса:

1. Дать студенту геометрическое образование.

2. Помочь овладеть теорией изображений, а это значит научиться решать две основные

Задачи курса:

1. Моделирование пространства - это умение по оригиналу построить его плоское изображение;

2. Реконструирование пространства - это умение по плоскому изображению восстановить оригинал.

Как Вы думаете?

Какие еще формы может принимать тень от треугольника?

В курсе элементарной геометрии изучается трехмерное пространство, названное евклидовым по имени греческого ученого Евклида, описавшего его основные своиства и закономерности. Однако положений евклидовой геометрии недостаточно для выполнения некоторых операций проецирования.

Развитие науки привело к расширению понятия пространства, так как вселенная представляется теперь состоящей из искривленных пространств. Это позволило дополнить привычное для нас евклидово пространство новыми элементами - бесконечно удаленной точкой, прямой, плоскостью. Для того, чтобы получить соответствующие элементы в тех случаях, когда их не оказывается при выполнении операции проецирования, достаточно потребовать, чтобы две параллельные прямые считались пересекающимися, при этом точку их пересечения называют несобственной точкой или бесконечно удаленной. Это понятие было введено в 1636 году французским математиком Жаном Дезаргом, графические доказательства [Фролов, стр. 14].

Будем считать, что:

1) две параллельные прямые пересекаются в единственной несобственной точке

m || n « m Ç n = М ¥

2) две параллельные плоскости пересекаются по единственной несобственной прямой:

S || Г « S Ç Г = а¥

Рис. 1-3

Рис. 1-4

Вывод.

Несобственные элементы позволяют создать более строгую теорию метода проецирования.

Методы проецирования

В этом разделе Вы освоите основной метод начертательной геометрии - проецирование. Рассмотрите центральное проецирование; параллельное проецирование; ортогональное проецирование.

Аппарат проецирования

Рис. 1-5

П₁ -плоскость проекций (картинная плоскость)

S - центр проецирования

А - точка в пространстве

А₁ - проекция точки

l_A - проецирующий луч

Спецификой курса начертательной геометрии является то, что изучение ведется на абстрактных геометрических фигурах: точка, линия, плоскость, поверхность. Мы будем изучать принципы построения изображений этих фигур на плоскости.

Прежде всего дадим определение простейшим геометрическим фигурам: точке и линии.

Точка - это нульмерная геометрическая фигура, неделимый элемент пространства, т.е. она не может быть определена другими более элементарными понятиями.

Обозначается - А,В,С...- прописными буквами латинского алфавита. или цифрами. Точка не имеет размеров, то что мы показываем на чертеже точку в виде какой - то площади, пересечением двух линий или кружочком, является лишь ее условным изображением.

Линия - одномерная геометрическая фигура, обозначается строчными буквами латинского алфавита - а,в,с...В начертательной геометрии линия определяется кинематически, как траектория непрерывно движущейся точки в пространстве, а рассматриваются следующие линии:

1. Прямая

2. Отрезок

3. Ломаная - состоящая из отрезков

4. Кривая

Центральное проецирование

Проецирование, когда проецирующий луч проходит через фиксированную точку S, называется центральным. На рис. 1-6 показано построение центральных проекций некоторых точек и прямой.

Рис. 1-6

П₁ -плоскость проекций (картинная плоскость)

S - центр проецирования

В, С, D - точки в пространстве

С₁, В₁, D₁ - проекции точек

l_B, l_C, l_D - проецирующие лучи

S - плоскость, проведенная через центр проецирования S и прямую а.

АМ - прямая в пространстве

А₁М₁ - проекция прямой (или отрезка)

Через точку S (центр проецирования) и точку В проведем проецирующий луч l_В, отметим точку пересечения проецирующего луча с картинной плоскостью: S Î l_В, B Î l_В, l_В Ç П₁ = В₁, на чертеже видно, что каждой точке пространства соответствует единственная проекция на плоскости.

Аналогично точке В можно построить проекцию любой точки пространства, например точки С

С₁ = l_С Ç П₁, если С Î П₁, то С = С₁.

Если l_D || П₁, то проекцией точки D Þ D₁ служит несобственная точка плоскости П₁.

По принципу центрального проецирования работают фото - и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования. Изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе архитекторы, дизайнеры, геологи и др.

Описанным методом центрального проецирования может быть построена проекция любой точки геометрической фигуры, а, следовательно, и проекция самой фигуры. Например , центральную проекцию отрезка АМ на плоскость П₁ можно построить как линию пересечения плоскости S, проведенной через центр S и прямую АВ, с плоскостью проекций. Так как две плоскости пересекаются по единственной прямой, то проекция прямой есть прямая, и притом, единственная, т. е. S É S, АМ; S Ç П₁ Þ А₁М₁.

Параллельное проецирование

Проецирование называется параллельным, если центр проецирования удален в бесконечность, а все проецирующие лучи параллельны заданному направлению s.

s - направление проецирования

Чтобы найти точку А₁ - параллельную проекцию точки А, построенную по направлению s на плоскости проекций П₁, нужно через точку А провести проецирующий луч l_A, параллельный прямой s, и определить точку его пересечения с плоскостью П₁:

l_A É A, l_A || s, l_A Ç П₁ = А₁

Точка А₁ является параллельной проекцией как для точки А, так и для точек А¹ и А²

Рис. 1-7

Свойства параллельных проекций

Геометрическая фигура в общем случае проецируется на плоскость проекций с искажением, но некоторые свойства оригинала сохраняются в проекциях при любом преобразовании и называются его инвариантами (остаются неизменными).

Метод Монжа

В машиностроительных чертежах используется метод прямоугольных проекций. Поэтому дальнейшее изучение курса будем вести, используя метод ортогонального проецирования.

Чтобы однозначно решить две основные задачи курса начертательной геометрии, чертежи должны удовлетворять следующим требованиям:

1. Простота и наглядность;

2. Обратимость чертежа.

Рассмотренные методы проецирования с использованием однокартинных чертежей позволяют решать прямую задачу (т.е. по данному оригиналу построить его проекцию). Однако, обратную задачу (т.е. по проекции воспроизвести оригинал) решить однозначно невозможно. Эта задача допускает бесчисленное множество решений, т.к. каждую точку А₁ плоскости проекций П₁ можно считать проекцией любой точки проецирующего луча l^А, проходящего через А₁. Таким образом, рассмотренные однокартинные чертежи не обладают свойством обратимости.

Для получения обратимых однокартинных чертежей их дополняют необходимыми данными. Существуют различные способы такого дополнения. Например, чертежи с числовыми отметками.

Способ заключается в том, что наряду с проекцией точки А₁ задаётся высота точки, т.е. её расстояние от плоскости проекций. Задают, также, масштаб. Такой способ используется в строительстве, архитектуре, геодезии и т. д. Однако, он не является универсальным для создания чертежей сложных пространственных форм.

Рис. 1-14

В 1798 году французский геометр-инженер Гаспар Монж обобщил накопленные к этому времени теоретические знания и опыт и впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения двух взаимно перпендикулярных плоскостей проекций. Отсюда ведёт начало принцип построения чертежей, которым мы пользуемся и поныне.

Поставим перед собой задачу построить проекции отрезка [AB] на две взаимно перпендикулярные плоскости проекций П₁ и П₂.

Пространственная модель.

Рис. 1-15

П₁ ^ П₂. AA₁ ^ П₁; |AA₁| - расстояние от А до П₁.

AA₂ ^ П₂; |AA₂|- расстояние от А до П₂.

П₁ - горизонтальная плоскость проекций;

П₂ - фронтальная плоскость проекций.

А₁В₁ - горизонтальная проекция отрезка;

А₂В₂ - фронтальная проекция отрезка.

х₁₂ - линия пересечения плоскостей проекций.

Однако, в таком виде чертёж неудобно читать. Поэтому Гаспар Монж предложил совместить эти плоскости проекций, причём, П принимается за плоскость чертежа, а П - поворачивается до совмещения с П₂. Такой чертёж называется комплексным чертежом.

Плоская модель.

Рассмотрим совмещение плоскостей проекций со всем их содержимым на плоском чертеже. Совокупность проекций множества точек пространства на П₁ называется горизонтальным полем проекций, а на П₂ - фронтальным полем проекций.

х₁₂ - ось проекций, база отсчёта.

Рис. 1-16

А₁А₂, В₁В₂ Þ линия связи - это прямая, соединяющая две проекции точки на комплексном чертеже. Линия связи перпендикулярна оси проекций.

Свойства двухкартинного комплексного чертежа Монжа:

1. Две проекции точки всегда лежат на одной линии связи установленного направления.

2. Все линии связи одного установленного направления параллельны между собой.

Безосный чертёж.

Если совмещённые плоскости П₁ и П₂ перемещать параллельно самим себе на произвольные расстояния ( см. положение осей х₁₂, х₁₂¹, х₁₂¹¹ на рис. 1-17), то будут меняться расстояния от фигуры до плоскостей проекций.

Рис. 1-17

Однако, сами проекции фигуры (в данном случае - отрезка АВ) при параллельном перемещении плоскостей проекций не меняются (согласно 7 свойству параллельного проецирования).

Из рис. 1-17 видно. что при любом положении оси х, величины DZ- разность расстояний от концов отрезка до П₁, и Dy -разность расстояний от концов отрезка до П₂, остаются неизменными. Поэтому нет необходимости указывать положение оси х₁₂ на комплексном чертеже и тем самым предопределять положение плоскостей проекций П₁ и П₂ в пространстве.

Это обстоятельство имеет место в чертежах, применяющихся в технике, и такой чертёж называется безосным.

Проиллюстрируем вышесказанное на конкретном примере.

Задача: Составить чертёж для изготовления стола (рис. 1-18).

1.Построить три проекции стола, учитывая свойства эпюра Монжа.

2. Что не хватает для выполнения по чертежу данного изделия?

3. Да, конечно, размеров.

Рис. 1-18а

Теперь, когда есть три изображения изделия и его размеры, имеют ли значение для изготовления изделия расстояния от изделия до плоскостей проекций, т. е. привязка к осям x, y и z (размеры 1500, 2000, 2000 на чертеже).

Нет не имеют!

По данному чертежу изделие создается, а на каком расстоянии его установить от стен (П₂,П₃) - это уже другая задача.

Рис. 1-18б

Безосный чертеж позволяет, не привязываясь к осям, располагать изображения в удобном для исполнителя положении, но с соблюдением проекционной связи, т.е. построение чертежа происходит по законам, установленным Гаспаром Монжем

Рис. 1-18в

Пространственный чертёж.

Рис. 1-19

1. AB - отрезок прямой в пространстве. A₁B₁ - горизонтальная проекция отрезка.

Через точку А проведём AВ¹ || А₁В₁. Тогда получим: 1. DАВВ¹ - прямоугольный;

2. АВ - гипотенуза треугольника - натуральная величина отрезка;

3. АВ¹ = А₁В₁ - один из катетов равен проекции отрезка АВ на плоскость проекций П₁.

4. Второй катет BВ¹ есть разность удалений концов отрезка от плоскости проекций П₁.

Проведя аналогичные рассуждения для плоскости проекций П₂, можно сделать вывод, что натуральная величина отрезка есть гипотенуза прямоугольного треугольника, одним из катетов которого является одна из проекций отрезка. Другой катет есть разность удалений концов отрезка от той плоскости, проекцию на которую взяли за первый катет.

Такой метод нахождения натуральной величины отрезка общего положения называют методом прямоугольного треугольника.

Плоский чертёж.

Дано: две проекции отрезка AB – А₂В₂ и А₁В₁ (рис. 1-20). Требуется определить натуральную величину этого отрезка.

Рис. 1-20

1. Исходя из вышесказанного, A₁B₁ является одним из катетов прямоугольного треугольника.

2. Чтобы найти второй катет, проведём A₂В¹ ^ линиям связи (рис.1-21). B₂B - это разность удалений концов отрезка от П₁.

Рис. 1-21

3. Откладываем расстояние |B₂В¹| на перпендикуляре к A₁B₁ с любой стороны.

5. Отрезок A₁B₀ - это натуральная величина |AB|, а угол a - есть угол наклона AB к П₁.

Аналогично, можно найти угол наклона данного отрезка к П₂, построив прямоугольный треугольник на П₂.

Вывод: Двухкартинный чертёж Монжа обратим.

Пространственный чертёж.

Рис. 1-22

П₃ ^ х, поэтому П₃ ^ П₁ и П₃ ^ П₂.

Три плоскости проекций образуют в пространстве прямоугольный трёхгранник, то есть систему трёх взаимно перпендикулярных плоскостей. Рёбра этого трёхгранника будем обозначать х, y, z.

П₃ - профильная плоскость проекций.

А₃ - профильная проекция точки А.

|AA₃| = |3A₂| = |2A₁| - удаление точки А от П₃.

Плоский чертёж.

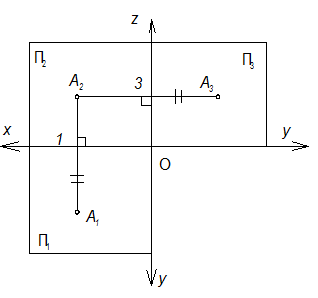
Рис. 1-23

A₁A₂ - линия связи в системе П₁ –П₂.

|3A₃| = |1А₁|.

A₂A₃ - линия связи в системе П₂ – П₃.

1А₂ - высота расположения точки,

1А₁ - глубина расположения точки,

3А₂ - ширина расположения точки.

х - абсцисса; y - ордината; z - аппликата.

Тест № 1

1. На каком чертеже точка В расположена дальше от наблюдателя, чем точки А и С?

2. В каком случае точка А принадлежит оси ОХ?

3. На каком чертеже точка С расположена выше точек А и В и дальше от наблюдателя?

4. Укажите чертёж фронтально конкурирующих точек.

5. На каком чертеже точки А и В одинаково удалены от плоскости проекций П₂?

6. В каком случае точка А принадлежит П₁.

7. Укажите чертёж горизонтально конкурирующих точек.

8. На каком чертеже точки А и В одинаково удалены от плоскости проекций П₁?

Комплексный чертеж линии

Кто совсем свободно знает (умеет проецировать)

прямую и плоскость, тот не встретит затруднений

в начертательной геометрии.

Г. Монж

В этом разделе Вы узнаете, что линии подразделяются на прямые и кривые. Проекции прямой линии могут занимать общее или частное положение относительно плоскостей проекций. Различают кривые линии плоские и пространственные; закономерные и незакономерные.

Как Вы думаете?

1. Как расположена прямая k в пространстве, если k₁ || k₂? (рис. 1-31)

2. Какая задана кривая на чертеже, плоская или пространственная? (ст. М1-29)

3. Как расположена прямая относительно плоскостей проекций, если сумма равных углов, которые она образует с П₁ и П₂ равны 90°? (рис. 1-32)

4. Сколько проекций должен иметь чертеж отрезка, чтобы его можно было назвать обратимым?

Задание прямой на комплексном чертеже

Прямая в пространстве может занимать общее и частное положение.

Прямые общего положения

Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения

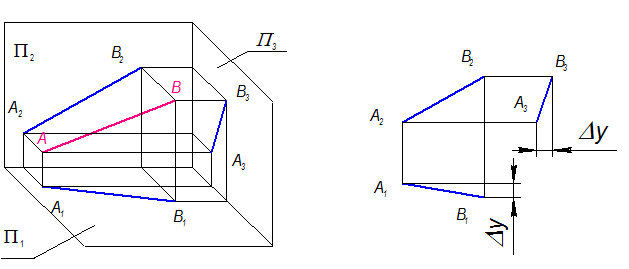
Рис. 1-30

Необходимо отметить особенности их задания на комплексном чертеже:

1. Любая проекция прямой общего положения искажает натуральную длину.

2. Любая проекция прямой общего положения наклонена к линиям связи под углом ¹ 90°, ни один из них не показывает натуральную величину углов наклона к плоскостям проекций.

3. Натуральная величина прямой общего положения находится методом прямоугольного треугольника

Примеры комплексных чертежей прямых общего положения:

Рис. 1-31

Прямая имеет одинаковые углы наклона к П₁ и П₂

Рис. 1-32

Точка пересечения проекций отрезка находится на оси X

Рис. 1-33

На безосных чертежах нет очертаний плоскостей проекций, но есть линии связи, поэтому положение геометрических фигур в пространстве будем определять положением их проекций относительно линий связи.

Графический признак прямой общего положения: ни одна из ее проекций не || и не ^ линиям связи

Прямые уровня

Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня.

Существует три линии уровня: h, f, p

Горизонталь

h (h₁, h₂, h₃) || П₃

Рис. 1-34

Если взять карандаш в руки и расположить его параллельно столу, то длина карандаша спроецируется на плоскость стола без искажения. У горизонтали | h | = | h₁ |, угол наклона к П₂ -b проецируется без искажения..

Графический признак горизонтали - ее фронтальная проекция перпендикулярна линиям связи (с нее всегда начинается построение чертежа горизонтали - h)

Фронталь

f (f₁, f₂, f₃) || П₂

Рис. 1-35

Если взять карандаш в руки и расположить его параллельно стене, находящейся перед наблюдателем, то длина карандаша спроецируется на плоскость стены без искажения. У фронтали | f | = | f ₂ |, угол наклона к П₁ - a cпроецируется без искажения.

Графический признак фронтали - ее горизонтальная проекция перпендикулярна линиям связи (с нее всегда начинается графическое построение фронтали - f)

Профильная прямая

р (р₁, р₂, р₃) || П₃

Рис. 1-36

| p | = | p₃ | - натуральная (истинная) величина

Углы наклона профильной прямой к П₁ и П₂ проецируются на П₃ без искажения.

Графический признак профильной прямой - ее горизонтальная и фронтальная проекции совпадают с линиями связи в системе П₁ – П₂.

Рассмотренные примеры позволяют отметить особенности задания прямых уровня на комплексном чертеже:

1. Одна из проекций прямых уровня перпендикулярна линиям связи установленного направления

2. Одна из проекций прямой уровня параллельна самой прямой и дает истинную величину, а также показывает без вспомогательных построений угол наклона к одной из плоскостей проекций (h, f), к двум плоскостям проекций (p).

Проецирующие прямые

Прямые, перпендикулярные какой - либо плоскости проекций, называются проецирующими прямыми.

Рис. 1-37

Фронтально проецирующая прямая

в(в₁, в₂, в₃) ^ П₂ (в || П₁ и П₃)

Рис. 1-38

Профильно проецирующая прямая

с(с₁, с₂, с₃) ^ П₃ (с || П₁ и П₂)

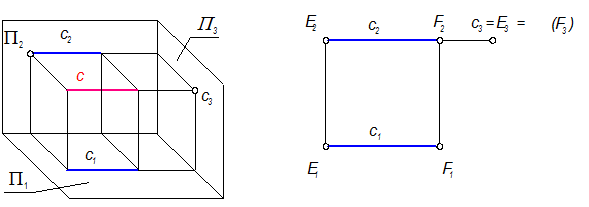
Рис. 1-39

Тест №2

1. Укажите чертежи прямых общего положения.

2. Укажите профильно проецирующую прямую.

3. Укажите горизонтально проецирующую прямую.

4. Укажите фронтально проецирующую прямую.

5. Укажите, в каком случае на чертеже можно замерить угол наклона прямой к П₁.

Как Вы думаете?

1. Могут ли проекции скрещивающихся прямых быть параллельны?

2. Могут ли проекции пересекающихся прямых изображены одной линией?

3. Имеют ли скрещивающиеся прямые общую точку, а их проекции?

Две прямые в пространстве могут:

1. пересекаться (а Ç в),

2. быть параллельными (а || в)

3. скрещиваться (а ° в).

Пресекающиеся прямые

Прямые называются пересекающимися, если они имеют единственную общую точку. Они всегда лежат в одной плоскости.

Рис. 1-40

Если прямые пересекаются, то существует единственная точка пересечения: а Ç в = К.

На основании свойства принадлежности: а Ç в = К Þ a₁ Ç в₁ = К₁, a₂ Ç в₂ = К₂

Согласно свойству чертежа Монжа, обе проекции (К₁ и К₂) точки К лежат на одной линии связи данного установленного направления.

Графический признак а Ç в: точки пересечения одноименных проекций лежат на одной линии связи, установленного направления.

Параллельные прямые

На основании свойства параллельности прямых (а || в) - одноименные проекции параллельных прямых параллельны:

а || в Þ a₁ || в₁, a₂ || в₂

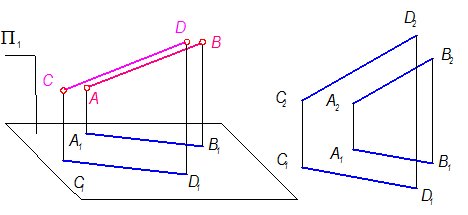
Рис. 1-41

Графический признак а || в: их одноименные проекции параллельны

Скрещивающиеся прямые

Если прямые не параллельны и не пересекаются, то они называются скрещивающимися прямыми. Через скрещивающиеся прямые невозможно провести плоскость, т.к. если одна прямая будет принадлежать плоскости, то другая будет пересекать эту плоскость (рис. 1-43)

Рис. 1-42

Сравнение:

Пересекающиеся прямые Скрещивающиеся прямые

Рис. 1-43

Точки А и В - горизонтально конкурирующие. С их помощью определяется видимость геометрических фигур на П₁ при решении задач. Из двух точек видна та, что выше.

Точки С и D - фронтально конкурирующие. С их помощью определяется видимость на П₂. Из двух точек видна та, что ближе к наблюдателю.

Рис. 1-44

Тест №3

Обучающий тест по теме - взаимное положение прямых на комплексном чертеже.

Ответы на этот тест Вы найдете в конце этого Модуля

1. Укажите чертеж пересекающихся прямых

2. Укажите чертежи параллельных прямых

3. Укажите чертежи скрещивающихся прямых

Справочный материал

Проиллюстрируем применение положений о взаимной принадлежности прямой и точки и взаимного расположения прямых при решении задач.

	1. Через точку А провести фронталь так, чтобы она пересекла прямую общего положения. f || П2, f É A, f Ç a
	2. Провести прямую а так, чтобы: а É А, а Ç m, а Ç n
	3. Построить точку В, горизонтально конкурирующую с точкой А и расположенную на 10мм выше точки А
	4. Построить точку С, фронтально конкурирующую с точкой М и расположенную ближе к наблюдателю на 15мм, а через нее провести прямую в параллельно заданной а.

Метод хорд

Линия считается заданной на чертеже, если известен закон нахождения каждой ее точки. Для задания линии удобно использовать ее определитель. Определитель линии - это минимальная информация, необходимая и достаточная для однозначного построения на эпюре любой точки кривой.

Построение на эпюре любой точки кривой позволит однозначно решить вопрос о характере кривой линии (плоская или пространственная). Если на заданной кривой взять произвольные четыре точки и через них провести хорды (секущие), то возможны два варианта:

1. Если хорды пересекаются (графически это видно на рис. 1-47, когда К₁, К₂ - точки пересечения проекций хорд лежат на одной линии связи), то через пересекающиеся прямые можно провести плоскость, а это значит, что они образуют плоскость, в которой лежит заданная кривая. Значит, кривая линия - плоская.

Плоская кривая линия

Рис. 1-47

2. Хорды не пересекаются, а скрещиваются (графически это видно на рис. 1-48, когда К₁, К₂ - точки пересечения проекций хорд не лежат на одной линии связи), значит кривая линия - пространственная.

Пространственная кривая линия

Рис. 1-48

Касательная, нормаль к кривой

Как построить касательную к кривой?

Для построения используем прямые, называемые секущими.

Прямая, пересекающая кривую линию в одной, двух и более точках, называется секущей (АВ).

Чтобы через точку А провести касательную t к кривой m, в окрестности точки А (недалеко) выбирают точку В и проводят секущую АВ. Приближая точку В к точке А в пределе получают касательную t в данной точке.

В ® А Þ АВ ® t

Рис. 1-49

Касательную (t в точке А) можно рассматривать как предельное положение секущей, которое занимает последняя при сближении точек пересечения А и В секущей АВ до слияния их в одну точку.

n - нормаль кривой линии в данной точке, n ^ t. Сколько их можно провести? К пространственной кривой можно провести n ® ¥, т.е. к касательной можно постро<