Задачи, приводящие к дифференциальным уравнениям.

Материальная точка массы m замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости V. Найти зависимость скорости от времени. Найти скорость точки через 3 с после начала замедления, если V(0) = 100 м/с, a V(l)= 50 м/с.

Решение: Примем за независимую переменную время t,отсчитываемое от начала замедления движения материальной точки. Тогда скорость точки V будет функцией t, т. е. V = V(t). Для нахождения V(t)воспользуемся вторым законом Ньютона (основным законом механики):
та=F, где а=V'(t) — есть ускорение движущегося тела, F — результирующая сила, действующая на тело в процессе движения.

В данном случае F =— kV², k > 0 —- коэффициент пропорциональности (знак минус указывает на то, что скорость тела уменьшается). Следовательно, функция V = V(t) является решением дифференциального уравнения тV' =— k V² или V' = —kV²/m. Здесь т — масса тела.

Из того, что , где с – const. Найдя зависимость скорости от времени, легко найти скорость точки через 3 с после начала замедления.

Найдем сначала параметры и с. Согласно условию задачи, имеем: V(0)= =100 и V(l)= = 50. Отсюда с = Следовательно, скорость точки изменяется по закону V = 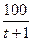. Поэтому V(3) = 25 м/с.

Дифференциальные уравнения первого порядка.

Определение.Дифференциальным уравнениемназывается уравнение, связывающее независимую переменную , искомую функцию и ее производные т.е. уравнения вида

(1)
где непрерывная функция переменных.

Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.

Например,

Если искомая функция зависит от нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Например,

В дальнейшем будем рассматривать лишь обыкновенные дифференциальные уравнения.

Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в уравнение.

Например: - дифференциальное уравнение 1- го порядка;

- дифференциальное уравнение 2- го порядка;

- уравнение 9- го порядка.

Решением дифференциального уравнения (1) называется функция которая при подстановке в дифференциальное уравнение обращает его в тождество.

Например, является решением дифференциального уравнения

В самом деле,

Процесс отыскания решений дифференциального уравнения называется интегрированием уравнения.График решения дифференциального уравнения называется интегральной кривойэтого уравнения.

Дифференциальные уравнения первого порядка

Общий вид уравнения первого порядка следующий:

(2)
Если уравнение (2) удается разрешить относительно , то получим

(3)
Это уравнение называется уравнением первого порядка,разрешенным относительно производной.

Рассмотрим дифференциальное уравнение вида

(4)
где правая часть есть произведение функции, зависящей только от , на функцию, зависящую только от .

Предполагая, что , преобразуем его следующим образом:

. ( )
Считая 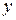известной функцией от , равенство ( ) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным слагаемым.

Интегрируя левую часть по , а правую по , получим

.

Мы получили соотношение, связывающее решение 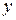, независимое переменное и произвольную постоянную , т.е. получили общий интеграл уравнения (4).

Дифференциальное уравнение типа ( ) или вида

(5)
называют уравнением с разделенными переменными.

Общий интеграл его есть

.

Уравнение вида

, (6)
в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от и только от 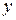, называется уравнением с разделяющимися переменными.

Путем деления обеих частей на произведение они приводятся к уравнениям с разделенными переменными:

или

,

т.е. к уравнению вида (5). Общий интеграл этого уравнения имеет вид

.

Определение 1. Функция 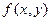называется однородной функцией -го измерения относительно переменных и 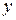, если при любом 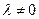справедливо тождество

.

Пример:

1) ;

- однородная функция первого измерения.

2) ;

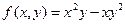- однородная функция третьего измерения.

3) ;

- однородная функция нулевого измерения.

Определение 2.Уравнение первого порядка

(7)
называется однородным уравнением, если функция 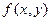есть однородная функция нулевого измерения относительно и .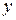

Метод решения однородного уравнения следующий. По условию . Положим в этом тождестве , получим , т.е. однородная функция нулевого измерения зависит только от отношения аргументов.

Уравнение (7) в этом случае примет вид

(8)
Сделаем подстановку , т.е. . Тогда будем иметь

.

Подставляя это выражение производной в уравнение (8) получим

.

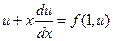Это уравнение с разделяющимися переменными:

, .

Интегрируя, найдем

.

Подставляя после интегрирования вместо отношение , получим интеграл уравнения (8).

Замечание. Уравнение вида будет однородным в том и только в том случае, когда и являются однородными функциями одного и того же измерения. Это вытекает из того, что отношение двух однородных функций – функций одного и того же измерения является однородной функцией нулевого измерения.

Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной вида

, (9)
где и - непрерывные функции от .

Будем искать решение уравнение (9) в виде произведения двух функций от

. (10)
Дифференцируя обе части равенства (10), находим

.

Подставляя полученное значение производной в уравнение (9), имеем

,

или

. (11)
Выберем функцию такой, чтобы

(12)
Разделяя переменные в этом дифференциальном уравнении, находим

, .

Интегрируя, получим

,

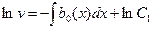или

.

Так как нам достаточно какого-нибудь отличного нуля решения уравнения (12), то за функцию возьмем

. (13)
Очевидно, что .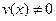

Подставляя найденное значение в (11) и, учитывая (12), получим

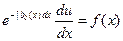
или ; .

Подставляя значения и в формулу (10), получаем

. (14)