Теоремы о выпуклости функции и точках перегиба

Теорема: (Об условиях выпуклости или вогнутости графика функции)

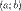Пусть функция определена на интервале и имеет непрерывную, не равную нулю в точке вторую производную. Тогда, если всюду на интервале , то функция имеет вогнутость на этом интервале, если 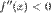, то функция имеет выпуклость.

Определение: Точкой перегиба графика функции называется точка , разделяющая промежутки выпуклости и вогнутости.

Теорема: (О необходимом условии существования точки перегиба)

Если функция имеет перегиб в точке , то 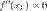или не существует.

Теорема: (О достаточном условии существования точки перегиба)

Если:

1. первая производная непрерывна в окрестности точки ;

2. вторая производная 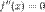или не существует в точке ;

3. при переходе через точку меняет свой знак, тогда в точке функция имеет перегиб.

Схема исследования функции на выпуклость, вогнутость

1. Найти вторую производную функции.

2. Найти точки, в которых вторая производная равна нулю или не существует.

3. Исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба.

13. Первообразная функции:

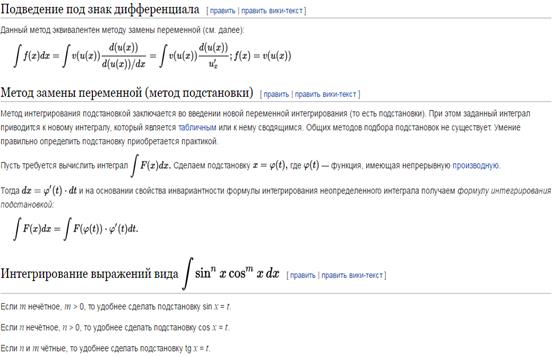Метод интегрирования, при котором интеграл путём тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

14. Алгебраические многочлены и рациональные дроби

15. Интегрирование иррациональных функций. Интегрирование некоторых тригонометрических выражений.

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Определенный интеграл – одно из основных понятий математического анализа – является мощным средством исследования в математике, физике, механике и других дисциплинах.

1.Вычисление площади криволинейной трапеции

Пусть на промежутке [a, b] задана функция f(x) 0. Криволинейной трапецией называется плоская фигура, ограниченная указанной кривой y = f(x), прямыми x = a, x = b и осью ОХ. (рис. 1). Для вычисления ее площади проделаем несколько операций.

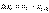1. Разобьем промежуток [a, b] произвольными точками на n частей. Положим , то есть есть длина i-го частичного отрезка, а наибольшую из этих длин обозначим , ( = max .

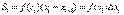2. На каждом отрезке [ возьмем по произвольной точке и вычислим Построим прямоугольник с основанием и высотой f( Его площадь равна Проделаем это для каждого i= 1, 2, …, n.

3. Площадь всей заштрихованной ступенчатой фигуры, составленной из прямоугольников, равна сумме Площадь криволинейной трапеции будет приближенно равна площади ступенчатой фигуры:

Чем мельче отрезки деления, тем точнее полученная фигура «отображает» криволинейную трапецию.

4. За площадь криволинейной трапеции принимают предел, к которому стремятся площади ступенчатых фигур, когда длины отрезков деления стремятся к нулю, а их число неограниченно увеличивается Таким образом, (1)

2) Вычисление пути, пройденного материальной точкой.

Пусть известен закон изменения мгновенной скорости . Определим путь, пройденный при движении точки за промежуток времени от до . Движение в общем случае предполагается неравномерным. Поступим следующим образом.

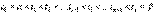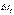1. Разобьем весь промежуток времени на n произвольных интервалов , где . На произвольном участке будем считать движение близким к равномерному с постоянной скоростью Тогда за время пройденный путь приближенно равен Результат справедлив для каждого интервала (i = 1, 2, …, n).

2. Если указанные интервалы достаточно малы, то весь путь приближенно равен сумме . Эта формула тем точнее, чем мельче разбиение данного промежутка времени.

3. Для получения точной формулы пути перейдем к пределу, увеличивая число дроблений 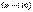и бесконечно измельчая сами интервалы. Обозначим 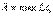, тогда (2)