
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА.
Будем предполагать, что все рассматриваемые ниже функции интегрируемы на заданных промежутках.
Свойство 1. 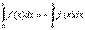 (6)
(6)
Для доказательства составим интегральные суммы (3) в обоих случаях с теми же точками деления. Они будут отличаться только знаком за счет знаков  : слева
: слева 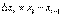 >0, справа
>0, справа 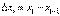 <0. Значит, в пределе получится нужное равенство.
<0. Значит, в пределе получится нужное равенство.
Свойство 2.  (7)
(7)
В этом случае отрезок интегрирования равен нулю и интегральная сумма – тоже.
Свойство 3.Постоянный множитель можно выносить за знак определенного интеграла: если  , то
, то
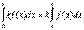 (8)
(8)
Доказательство:
 (см.(4)) =
(см.(4)) = 
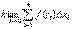 = =
= = 
Свойство 4.Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от этих функций:  (9)
(9)
Свойство 5.Если отрезок [a, b] разбит точкой с на две части [a, c] и [c, b], то  (10)
(10)
 Доказательство. Составим интегральную сумму для
Доказательство. Составим интегральную сумму для  на [a, b]. Так как предел этих сумм не зависит от способа разбиения [a, b] на части, то рассмотрим только те разбиения, в которых точка с входит в качестве точки деления. Тогда
на [a, b]. Так как предел этих сумм не зависит от способа разбиения [a, b] на части, то рассмотрим только те разбиения, в которых точка с входит в качестве точки деления. Тогда  , где
, где  - суммы, соответствующие отрезкам [a, c] и [c, b]. Переходя в последнем равенстве к пределу при
- суммы, соответствующие отрезкам [a, c] и [c, b]. Переходя в последнем равенстве к пределу при  , получим соотношение (10).
, получим соотношение (10).
Замечание.Свойство сохраняется при любом взаимном расположении точек a, b, c. На рисунке 2. дана геометрическая иллюстрация свойства 5 для случая, когда  и a < c < b: площадь трапеции aABb равна сумме площадей трапеций aACc и cCBb.
и a < c < b: площадь трапеции aABb равна сумме площадей трапеций aACc и cCBb.
Свойство 6.Если всюду на отрезке [a, b] функция неотрицательна  то
то  а если
а если 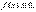 то
то 

 Доказательство. В самом деле, любая интегральная сумма
Доказательство. В самом деле, любая интегральная сумма 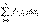 для
для 
 на [a, b] неотрицательна, так как
на [a, b] неотрицательна, так как 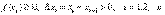 Переходя к пределу в неравенстве
Переходя к пределу в неравенстве  , получаем
, получаем 
Для случая  на [a, b] доказательство аналогичное.
на [a, b] доказательство аналогичное.
Геометрический смысл утверждения очевиден.
Следствие из свойств 5 и 6.
Интегрирование в симметричных пределах можно упростить, если воспользоваться формулами:
 a)
a)  , если
, если 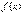 - четная функция,
- четная функция,
б)  , если
, если  - нечетная функция.
- нечетная функция.
Эти утверждения наглядно иллюстрируются геометрически (рис. 3).
Свойство 7.(Интегрирование неравенств).
Если на отрезке [a, b] функции  и
и  удовлетворяют условию
удовлетворяют условию 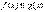 , то
, то  (11).
(11).
Доказательство. На отрезке [a, b] разность  , тогда по свойству 6 :
, тогда по свойству 6 :  Применим затем свойство 4:
Применим затем свойство 4:  Отсюда следует неравенство (11).
Отсюда следует неравенство (11).
Если  >0 и
>0 и  >0 на [a, b], то свойство 7 иллюстрируется геометрически (рис. 4). Так как
>0 на [a, b], то свойство 7 иллюстрируется геометрически (рис. 4). Так как  , то площадь криволинейной трапеции
, то площадь криволинейной трапеции  не больше площади
не больше площади  .
.
Свойство 8.(Оценка определенного интеграла). Если на отрезке [a, b] функция удовлетворяет условию  , то определенный интеграл удовлетворяет неравенству
, то определенный интеграл удовлетворяет неравенству  (12)
(12)
Доказательство.
Предварительно вычислим с помощью интегральной суммы 
По условию  Проинтегрируем данное неравенство, используя свойство 7:
Проинтегрируем данное неравенство, используя свойство 7:  . Затем, используя свойство 3 и только что полученный результат, имеем
. Затем, используя свойство 3 и только что полученный результат, имеем  Подставляя их в предыдущее неравенство, получим нужное неравенство (12). Если
Подставляя их в предыдущее неравенство, получим нужное неравенство (12). Если  , то свойство имеет простую геометрическую ллюстрацию (рис. 5. ): площадь криволинейной трапеции AABb заключена между площадями двух прямоугольников
, то свойство имеет простую геометрическую ллюстрацию (рис. 5. ): площадь криволинейной трапеции AABb заключена между площадями двух прямоугольников 
Свойство 9.(Теорема о среднем).
Определенный интеграл от функции  , непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка:
, непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка:  (13).
(13).
Доказательство.
По свойству функций, непрерывных на отрезке  достигает своего наименьшего
достигает своего наименьшего  и наибольшего
и наибольшего  значений и принимает все промежуточные значения между
значений и принимает все промежуточные значения между  и
и  :
:  . В силу формулы (12), предположив, что a<b , имеем
. В силу формулы (12), предположив, что a<b , имеем 
Обозначим  тогда
тогда  По свойству непрерывных функций найдется значение
По свойству непрерывных функций найдется значение  такое, что
такое, что  ,
,
 Следовательно, из равенства
Следовательно, из равенства  (14) получим нужное соотношение (13).
(14) получим нужное соотношение (13).
Замечание.В выражении (14)  называют средним (средним интегральным) значением функции
называют средним (средним интегральным) значением функции 
 на отрезке
на отрезке 
Геометрический смысл среднего значения  показан на рис. 6. Значение
показан на рис. 6. Значение  должно быть таким, чтобы площадь прямоугольника
должно быть таким, чтобы площадь прямоугольника  равнялась площади криволинейной трапеции
равнялась площади криволинейной трапеции 
Заметим, что теорема говорит о существовании точки  ,
,  но не дает способа ее нахождения.
но не дает способа ее нахождения.
Свойство 10.Абсолютное значение интеграла не превосходит интеграла от абсолютного значения функции: 
Доказательство.
Это неравенство получится, если для интегральной суммы (3) записать, что абсолютное значение суммы не превосходит суммы абсолютных значений  , а затем перейти к пределу.
, а затем перейти к пределу.
Несобственный интеграл.
Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий.
-Область интегрирования является бесконечной. Например, является бесконечным промежутком
{\displaystyle [a,+\infty )}-Функция {\displaystyle f(x)} является неограниченной в окрестности некоторых точек области интегрирования.
Если интервал {\displaystyle [a,b]} конечный, и функция интегрируема по Риману, то значение несобственного интеграла совпадает с значением определённого интеграла.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...