Алгоритм решения уравнения в полных дифференциалах

1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:

2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):

3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:

4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:

Отсюда получаем выражение для производной неизвестной функции φ(y):

5. Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):

6. Общее решение уравнения в полных дифференциалах записывается в виде:

Решение линейных уравнений первого порядка, метод вариации постоянной, метод Бернулли.

, где p(x) и g(x) – непрерывные функции (постоянные, в частности) – линейные ур-ия 1-го порядка. Существует три способа решения этого уравнения:

* метод интегрирующего множителя;

* метод введения двух функций (Бернулли);

* метод вариации постоянной (Лагранжа).

Использование интегрирующего множителя

Если линейное дифференциальное уравнение записано в стандартной форме:

то интегрирующий множитель определяется формулой: .

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения Общее решение дифференциального уравнения выражается в виде: 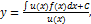где C − произвольная постоянная.

Метод вариации постоянной

Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения: .

Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x).
Найдём сначала общее решение ур-ия , т.е.

Разделяя переменные, имеем: ,

Т.е. . Общее решение заданного уравнения ищем в виде . Подставляя y и в данное уравнения, получим:

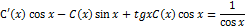
Отсюда 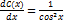; ; 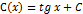=> общее решение ур-ия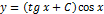

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде ,

где и − непрерывные функции.

Если m=0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когда m=1, уравнение преобразуется в уравнение с разделяющимися переменными.
В общем случае, когда m≠0,1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки .

Новое дифференциальное уравнение для функции z(x) имеет вид

и может быть решено способами, описанными выше.

54. Линейные однородные дифференциальные уравнения второго порядка.

Рассмотрим линейное дифференциальное уравнение вида ,

где − постоянные коэффициенты.

Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: .

Общее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:

1. Дискриминант характеристического квадратного уравнения положителен: . Тогда корни характеристического уравнения и действительны и различны. В этом случае общее решение описывается функцией , где C1 и C2 − произвольные действительные числа.

2. Дискриминант характеристического квадратного уравнения равен нулю: D=0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:

3. Дискриминант характеристического квадратного уравнения отрицателен: D<0. Такое уравнение имеет комплексно-сопряженные корни . Общее решение записывается в виде

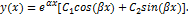
Рассмотренные три случая удобно представить в виде таблицы: