
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Наближене розв’язування рівнянь
Графічне зображення функцій дає можливість легко знайти наближений розв’язок будь-якого рівняння з однією змінною і системи двох рівнянь з двома змінними.
Приклад. Розв’язати рівняння  . Це рівняння не зводиться до алгебраїчного .Один корінь(х = 4 ) легко підібрати .Щоб знайти інші корені ( якщо вони є ) краще розв’язати графічно. Замінимо задане рівняння системою у = 2х , у = 4х. Побудуємо графік показникової функції у = 2х і функції у = 4х ( пряма лінія ) . В перетині знаходимо дві точки А і В. Абсциса точки А є х = 4 , абсциса точки В є х ≈ 0,3 . Знайдено розв’язок даного рівняння .
. Це рівняння не зводиться до алгебраїчного .Один корінь(х = 4 ) легко підібрати .Щоб знайти інші корені ( якщо вони є ) краще розв’язати графічно. Замінимо задане рівняння системою у = 2х , у = 4х. Побудуємо графік показникової функції у = 2х і функції у = 4х ( пряма лінія ) . В перетині знаходимо дві точки А і В. Абсциса точки А є х = 4 , абсциса точки В є х ≈ 0,3 . Знайдено розв’язок даного рівняння .
Функції, неперервні на відрізку, мають ряд властивостей , які мають теоретичне і практичне значення.
Властивість функції неперервної на відрізку .
Теорема . Якщо функція y=f(x) неперервна на відрізку  і на його кінцях приймає значення різних знаків , то існує хоча б одна точка з проміжку
і на його кінцях приймає значення різних знаків , то існує хоча б одна точка з проміжку  , в якій f(x)=0.
, в якій f(x)=0.
| X |
| Y |
| α |
| b |
| b1 |
| α1 |
Рис. 8
З даної теореми одержуємо метод ( який називають методом «половинного поділу») знаходження кореня рівняння f(x)=0, якщо відомо , що він має єдиний корінь на відрізку  , f(x) неперервна на цьому відрізку і на його кінцях приймає значення різних знаків . При цьому поступають наступним чином. Обчисляють значення функції f(x) в середині відрізка
, f(x) неперервна на цьому відрізку і на його кінцях приймає значення різних знаків . При цьому поступають наступним чином. Обчисляють значення функції f(x) в середині відрізка  . Якщо
. Якщо  = 0, то корінь знайдено. Якщо
= 0, то корінь знайдено. Якщо  ≠ 0 , то для дальших обчислень вибирається та із двох одержаних половинок , на кінцях якої f(x) приймає значення різних знаків . Повторюючи ті самі міркування , ми все ближче наближаємось до кореня рівняння f(x)=0.
≠ 0 , то для дальших обчислень вибирається та із двох одержаних половинок , на кінцях якої f(x) приймає значення різних знаків . Повторюючи ті самі міркування , ми все ближче наближаємось до кореня рівняння f(x)=0.
Приклад . Для рівняння х3 - х2 – х – 2 =0 відомо, що воно має єдиний корінь на відрізку 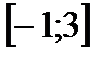 . Знайти цей корінь .
. Знайти цей корінь .
Нехай f(x)= х3 - х2 – х – 2.Так як f(-x)=-3<0, f(3)=13>0 і f(x) неперервна на [-1;3] , то можна застосувати метод половинного поділу. Обчисляємо значення функції в середині відрізка [-1;3] ;
 < 0. Оскільки f(1) < 0, то розглянемо відрізок [1;3]. Обчислимо значення функції f(x) в середині одержаного відрізка :
< 0. Оскільки f(1) < 0, то розглянемо відрізок [1;3]. Обчислимо значення функції f(x) в середині одержаного відрізка :  . Отже , х=2 – шуканий корінь .
. Отже , х=2 – шуканий корінь .
Вправи
99. Визначить графічно, скільки коренів має рівняння:
1) х3=1-  ; 2) 2х=2-х2; 3)
; 2) 2х=2-х2; 3) 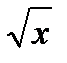 =(х-3)2; 4) sinx=
=(х-3)2; 4) sinx=  ;
;
5) cosx =  ,
,  .
.
100. При яких значеннях а рівняння 1)  не має розв’язків? Має єдиний розв’язок? Має два розв’язки ? Має більше двох розв’язків ?
не має розв’язків? Має єдиний розв’язок? Має два розв’язки ? Має більше двох розв’язків ?
Границя і неперервність функції
1. Неперервні функції, їх властивості. Число А називається границею функції y=f(x) при х→х0 , якщо для будь-якого додатного числа  можна вказати такий окіл точки х0 , що для всіх х≠х0 із цього околу виконується нерівність
можна вказати такий окіл точки х0 , що для всіх х≠х0 із цього околу виконується нерівність  <
<  . Пишуть
. Пишуть 
При обчисленні границь користуються наступними правилами: якщо існують 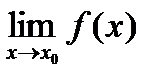 і
і  , то
, то
1) 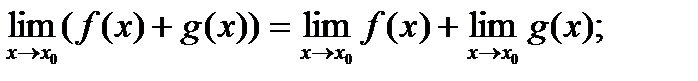
2)  де к− стала ;
де к− стала ;
3) 
4)  при умові , що
при умові , що  .
.
Для розкриття деяких невизначеностей можна скористуватися наступними «чудовими» границями :
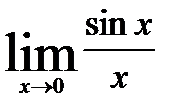 ;
;  ;
; 
 = ℮ (℮ = 2,71…)
= ℮ (℮ = 2,71…)
Функція y=f(x) називається неперервною в точці х0 , якщо: а) вона визначена в цій точці; б) існує границя  ; в) ця границя дорівнює значенню функції в точці х0.
; в) ця границя дорівнює значенню функції в точці х0.
Функція, неперервна в кожній точці проміжку, називається неперервною на цьому проміжку. Якщо неперервність функції порушується в деякій точці, то цю точку називають точкою розриву функції.
Степенева, показникова, логарифмічна, тригонометрична функції неперервні в своїх областях визначення.
Вправи
101. Знайти границі функцій :
1)  ; 2)
; 2)  ; 3)
; 3) 
4)  ; 5)
; 5)  6)
6) 
7)  8)
8)  ; 9)
; 9) 
10)  11)
11)  12)
12) 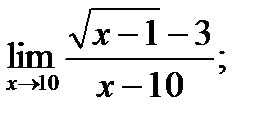
13)  14)
14) 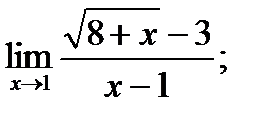 15)
15) 
16)  17)
17)  18)
18) 
19)  20)
20)  21)
21) 
22)  23)
23) 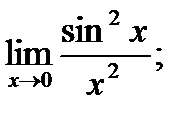 24)
24)  25)
25) 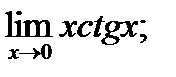 26)
26)  27)
27) 
28) 

Запитання для самоконтролю
1. Дайте означення границі змінної величини . Перелічіть властивості границь .
2. Дайте означення границі функції в точці .
3. Дайте означення неперервної функції . Які властивості на відрізку вона має ? Визначити проміжки неперервності функції  .
.
4. Поясніть основний метод розкриття невизначеності  .
.
5. Сформулюйте і запишіть першу і другу визначну границю.
Глава 6. Похідна і її застосування
Похідні і диференціали функцій
1. Похідна , її фізичний і геометричний зміст.
▪ 1. Означення похідної .
▪ 2. Фізичний зміст похідної.
▪ 3. Геометричний зміст похідної.
▪ 4. Рівняння дотичної.
▪ 5. Таблиця похідних .
▪ 6. Правила диференціювання.
▪ 7. Похідні вищих порядків.
▪ 8. Диференціал функції і його застосування до наближених обчислень.
Похідною функції y=f(x) в точці х0 називається границя відношення приросту функції до приросту аргументу ∆х=х-х0, коли приріст аргументу прямує до нуля. Позначається 
З погляду фізикипохідна має таке тлумачення:
а) швидкість руху v= 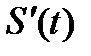 , де S─ шлях, t─ час;
, де S─ шлях, t─ час;
б) лінійна густина  , де m─ маса стержня, l─ довжина;
, де m─ маса стержня, l─ довжина;
в) сила струму I=  , де Q ─ кількість електрики, що проходить через провідник, t─ час;
, де Q ─ кількість електрики, що проходить через провідник, t─ час;
г) теплоємкість C=  , де
, де  ─ кількість теплоти; t─ температура.
─ кількість теплоти; t─ температура.
Геометричний зміст похідної. Якщо функція y=f(x) диференційована в точці х0 , то існує дотична до її графіка в точці (x0; f(x0)), кутовий коефіцієнт якої дорівнює 
Рівняння дотичноїмає вигляд: y=f(x0)+ 
Наведемо таблицю похідних елементарних функцій:
1)  ( с – стала) ; 8)
( с – стала) ; 8) 
2)  9)
9) 
3)  10)
10) 
4)  11)
11) 
5)  12)
12) 
6)  13)
13) 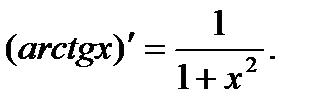
7)  14)
14) 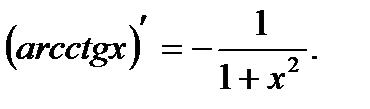
Правила диференціювання
1. 
2.  де к─ стала;
де к─ стала;
3. 
4.  ;
;
5.  де u=g(x).
де u=g(x).
Похідна від похідної функції називається її другою похідною, або похідною другого порядку , і позначається  .
.
Аналогічно 
Прискорення прямолінійного руху тіла в даний момент дорівнює другій похідній шляху по часу, обчисленого для даного моменту .
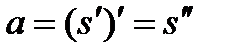
2. Диференціал функції. Застосування диференціала до наближених обчислень.
Якщо функція y=f(x) диференційована в точці х0, то вираз виду  де ∆х=х-х0 , називається диференціалом функції в точці х0 і позначається df (x0) або dy (x0). Диференціал незалежної змінної dx вважають рівним його приросту ∆х, тому
де ∆х=х-х0 , називається диференціалом функції в точці х0 і позначається df (x0) або dy (x0). Диференціал незалежної змінної dx вважають рівним його приросту ∆х, тому
df(x0)=  .
.
Якщо провести дотичну до графіка функції y=f(x) в точці (x0; f(x0)), то диференціал дорівнює приросту ординати цієї дотичної.
Якщо  то значення функції y=f(x) в точці х близькій до х0 , можна наближено обчислити по формулі :
то значення функції y=f(x) в точці х близькій до х0 , можна наближено обчислити по формулі : 
Приклад. Обчислити значення функції у=х3+х2-2х при х=3,02.
х=3+0,02, звідки х0= 3 , ∆х=0,02.
Знайдемо похідну функції: y/ =3x2+2x-2, знайдемо значення функції і похідної в точці х0=3. у(3) =33+32-2 ∙3=30,
y/(3)= 3∙32+2∙3-2=31. Дані обчислень підставимо у формулу і отримаємо: у(3,02) ≈ 30+31∙0,02=30,62.
Вправи
102. Знайти похідні наступних функцій:
1) у= 3х-2 ; 2) у= 2х1/4 ; 3) у= 3  ; 4) у= 5
; 4) у= 5  ; 5) у=
; 5) у=  ; 6) у=
; 6) у=  7) у=
7) у=  ; 8) у=
; 8) у= 
9) у=  ; 10) у=
; 10) у= 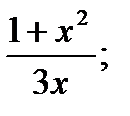 11) у=
11) у=  12) у=
12) у=  13) у=(9-х2)4 ; 14) у=(х4-х-1)4; 15) у=
13) у=(9-х2)4 ; 14) у=(х4-х-1)4; 15) у=  16) у= sin5x;
16) у= sin5x;
17) y= sin23x; 18) y= lnx3; 19) y= ln(x2-1);
20) y= lnsin3x; 21) y=ln2sin2x; 22) y=  ;
;
23) y= 3x; 24) y= x3+2x; 25) y= 2sin5x; 26) y= 32sin2x ;
27) y= 3sinx – 22x + x2; 28) y= sin (x3-3x2); 29) y= sin4x;
30) y=sin25x ; 31) y= lnsinx; 32) y= lnsin23x;
33) y=cos(x2-3x); 34) y=cos35x ; 35)y=sin23x-cos23x;
36) y=3 lncos2x; 37) y=tgx5; 38) y=ctg3x; 39) y=tglnx; 40) y= lntg3x; 41) y=cosx4;
42) y=(z2+1)sin3x; 43) y= (x+2)ln5x; 44) y=  ; 45) y=tg52x-cos32x+sinx2; 46) y= (x3-2)(x2+x+1);
; 45) y=tg52x-cos32x+sinx2; 46) y= (x3-2)(x2+x+1);
103. Знайти кутовий коефіцієнт дотичної, проведеної до кривої у=х3 в точці С(-2; -8).
104. Скласти рівняння дотичної до параболи у=х2-4х в точці з абсцисою х0=1.
105. Знайти кути, під якими парабола у=х2-х перетинає вісь абсцис.
106. Знайти кутовий коефіцієнт дотичної до параболи у=х2-3 при х=1/2.
107. Шлях, пройдений матеріальною точкою, задається наступною функцією часу: s=3t2-2t+4. Знайти швидкість руху точки в кінці 5-ї секунди.
108. Точка рухається прямолінійно по закону s=2t3+t2-4. Знайти її швидкість в момент часу t=4.
109. Точка рухається прямолінійно по закону s=6t-t2. В який момент її швидкість буде рівною нулю?
110. Два тіла рухаються прямолінійно: одне по закону s=t3+t2-27t, а друге ─ по закону s=t2+1. Визначить момент, коли швидкості цих тіл будуть рівними.
111. Кількість електрики, що протікає через провідник, починаючи з моменту часу t=0, задається формулою
Q=3t2-3t+4. Знайти силу струму в кінці 6-ї секунди.
112. Зміну сили струму I в залежності від часу t задано рівнянням I=2t2-5t . Знайти швидкість зміни сили струму в кінці 10-ї секунди.
113. Температура тіла T змінюється в залежності від часу t по закону T=0,5t2-2t. З якою швидкістю нагрівається це тіло в момент часу t=5c?
114. Знайти диференціали функцій:
1) у=  ; 2) у=
; 2) у= 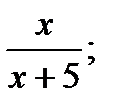 3) у=(х2-1)(х+2);
3) у=(х2-1)(х+2);
4) у=sin5x ; 5) y= cos2x; 6) y=lncosx .
115. Користуючись поняттям диференціала функції, обчисліть наближено значення функції у=х3-7х2+80 при зміні аргументу х від 5 до 5,01.
116. Обчислити наближено значення функції f(x)=x5+2x4-x3-1 в точці х=1,01.
117. Знайти наближене значення :  .
.
Запитання для самоконтролю
1. Дати означення похідної заданої функції.
2. Охарактеризувати символи 
3. Який геометричний, механічний і фізичний зміст похідної?
3. Як знайти похідну, виходячи з її означення?
4. Дотична до кривої y=f(x) в точці М0(х0,у0) нахилена під кутом  . Чому дорівнює
. Чому дорівнює 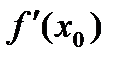 ?
?
5. Дотична до кривої y=f(x) в точці М0(х0,у0) паралельна осі Ох. Чому дорівнює  ?
?
6. Що називається диференціалом функції? Як визначається диференціал функції через її похідну?
7. Який геометричний та механічний зміст диференціала?
8. Обґрунтувати формулу для наближеного обчислення значення функції за допомогою диференціала.
Застосування похідної
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...