
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Що називається скалярним полем?
2. Яке поле називається стаціонарним і нестаціонарним?
3. Записати формулу для похідної за напрямом функції
U = f(x,y,z).
4. У чому полягає фізичний зміст похідної за напрямом?
5. Дати означення градієнта скалярного поля.
6. Сформулювати необхідні умови існування екстремуму функції z = f (x,y).
7. Сформулювати достатні умови існування екстремуму функції z = f (x,y).
8. Що називається стаціонарними точками функції
z = f (x,y)?
9. Коли функція z = f (x,y) має екстремум?
Глава 8. Інтеграл і його застосування
§1. Невизначений інтеграл
1. Невизначений інтеграл і його властивості.
Означення 1.Функція y=F(x) називається первісною для функції y=f(x) на деякому проміжку, якщо для всіх х із цього проміжку  .
.
Якщо y=F(x)─ первісна для функції y=f(x) на деякому проміжку, то існує нескінченно багато первісних для y=f(x) на цьому проміжку, і всі вони мають вигляд y=F(x)+C, де С─ довільна стала. Геометрично це означає, що графіки всіх первісних можна одержати із графіка якоїсь однієї з них переміщенням цього графіка вздовж осі у.
Означення 2.Сукупність первісних y=F(x)+C для функції y=f(x) на деякому проміжку називається невизначеним інтегралом функції на цьому проміжку і позначається символом ∫ f(x)dx=F(x)+C.
Знаходження невизначеного інтеграла називають інтегруванням функції.
Таблиця основних інтегралів .
1) ∫ хаdx=  2)
2) 
3) 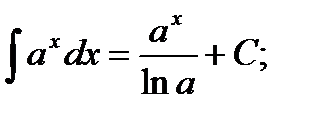 4) ∫ ℮xdx=℮x+C;
4) ∫ ℮xdx=℮x+C;
5) ∫ cos x dx= sin x+C; 6) ∫ sin x dx = - cos x+C;
7)  8)
8) 
9)  10)
10) 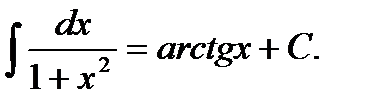
Щоб знайти невизначений інтеграл, достатньо звести його до табличного. Це часто вдається зробити шляхом перетворення підінтегрального виразу і застосування основних правил інтегрування:
1) ∫ kf(x)dx=k∫ f(x)dx, де к─ стала;
2) ∫ (f(x)± g(x))dx= ∫ f(x)dx ± ∫ g(x)dx;
3) ∫ f(kx+b)dx=  де k і b─ сталі.
де k і b─ сталі.
Вправи
133. Знайти первісну функції: 1) f(x)=3x2; 2) f(x)=x6; 3) f(x)=8x7.
134. Перевірити, що функція F(x)=x5+3x2-cosх є первісною функції f(x)=5x4+6x+sinx.
135. Знайти інтеграли:
1) ∫ х6dx; 2) ∫ 8x3dx; 3) ∫ 
4)  5)
5)  dx; 6) ∫ x2/3dx;
dx; 6) ∫ x2/3dx;
7) ∫ (5x3-2x2+3x-8)dx; 8) ∫ x3(1+5x)dx; 9) ∫(2x-3)3dx;
10) ∫ (  11) ∫
11) ∫  12) ∫
12) ∫ 
13)  14)
14)  15)
15) 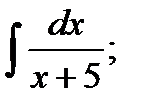
16) ∫ (x5+3℮x)dx; 17) ∫ (x3+2x)dx; 18) ∫ sin2xdx;
19)  20)
20)  21)
21)  22)
22)  ; 23)
; 23) 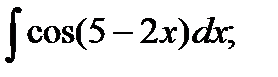 24)
24) 
25)  26)
26)  27) ∫ tg2dx;
27) ∫ tg2dx;
28)  29)
29)  30)
30)  .
.
Запитання для самоконтролю
1. Яка функція називається первісною для заданої функції ?
2. Запишіть первісні для функцій : 3 ; 4х3 ; cos x ; 2/x.
3. Чому при інтегруванні функцій появляється довільна стала ?
4. Як записують цілу сукупність первісних ?
5. Що називається невизначеним інтегралом ?
6. Чим відрізняється невизначений інтеграл від первісної функції ?
7. Чому інтеграл називають невизначеним ?
8. Чому дорівнює інтеграл від диференціала деякої функції?
9. Як перевірити результат інтегрування ?
10. В чому полягає геометричний зміст невизначеного інтеграла?
11. Що таке інтегральні криві ? Як вони розміщені одна відносно одної ? Чи можуть вони перетинатися ?
12. Як із сімейства інтегральних кривих виділити одну із них?
Інтегрування підстановкою і по частинах
▪ Спосіб підстановки (заміни змінної)
▪ Приклади інтегрування підстановкою
▪ Спосіб інтегрування по частинах
1. Спосіб підстановки (заміни змінної)
Якщо заданий інтеграл за допомогою алгебраїчних перетворень важко або неможливо звести до табличного інтеграла, то для його знаходження застосовують інші способи, одним із яких є спосіб підстановки (заміни змінної).
Спосіб підстановки полягає в слідуючому: замінюють новою змінною таку частину підінтегральної функції, при диференціюванні якої одержується частина підінтегрального виразу, що залишилася ( не враховуючи сталого множника).
Приклад1.  =
= 
Вправи
136. Знайти невизначений інтеграл:
1) ∫ (2х+3)4dx; 2) ∫(7-2t)3dt; 3) ∫ 
4)  5)
5)  6)
6) 
8)  9)
9)  10)
10) 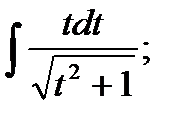 12)
12)  13)
13)  14)
14) 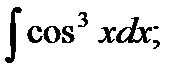
15)  16)
16)  17)
17)  18)
18)  19)
19)  20)
20) 
21)  22)
22) 
23)  24)
24) 
При інтегруванні функцій, що містять добуток, логарифми і обернені тригонометричні функції, буває зручно скористуватися способом інтегрування по частинах.
Формула інтегрування по частинах:  (1)
(1)
Вкажемо деякі типи інтегралів, які зручно обчислювати методом інтегрування частинами:
1) інтеграли виду  де Р(х)─ многочлен.
де Р(х)─ многочлен.
У цих інтегралах за u слід взяти множник Р(х), а за
dv ─ вираз, що залишився.
2) інтеграл виду  де Р(х)─ многочлен. У цих інтегралах слід взяти dv=P(x)dx;
де Р(х)─ многочлен. У цих інтегралах слід взяти dv=P(x)dx;
3) інтеграли виду: 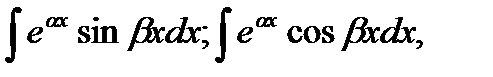 де
де  ─ дійсні числа. Тут після двократного застосування формули (1) утворюється лінійне рівняння відносно шуканого інтеграла. Розв’язуючи це рівняння, знаходять інтеграл.
─ дійсні числа. Тут після двократного застосування формули (1) утворюється лінійне рівняння відносно шуканого інтеграла. Розв’язуючи це рівняння, знаходять інтеграл.
Приклад 2. 
Вправи
137.Знайти інтеграли:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8)  9)
9)  10)
10) 
Визначений інтеграл
Нехай на відрізку [a,b] визначена функція f(x) . Розіб’ємо відрізок [a,b] на n частин точками a = x0<x1<…<xn = b. На кожному проміжку ( хі-1, хі ) візьмемо довільну точку  і складемо суму
і складемо суму  , де ∆ хі =хі –хі-1. Така сума називається інтегральною.
, де ∆ хі =хі –хі-1. Така сума називається інтегральною.
Означення.Якщо існує скінченна границя інтегральної суми при  , то вона називається визначеним інтегралом від функції f(x) в межах від а до b і позначається
, то вона називається визначеним інтегралом від функції f(x) в межах від а до b і позначається
 , а функція f(x) називається інтегрованою на [a,b].
, а функція f(x) називається інтегрованою на [a,b].
1. Формула Ньютона - Лейбніца. Основні властивості визначеного інтеграла.
Визначений інтеграл від неперервної функції y=f(x) дорівнює приросту первісної y=F(x) для цієї функції на вказаному проміжку, тобто
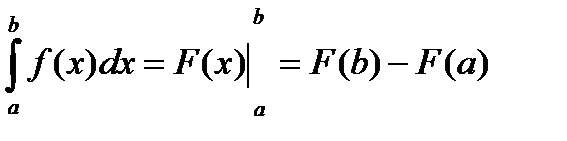 (формула Ньютона-Лейбніца).
(формула Ньютона-Лейбніца).
Властивості визначеного інтеграла:
1)  , де к─ стала;
, де к─ стала;
2) 
3)  де
де 
4) 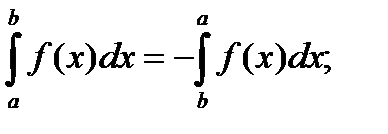
5) 
Приклад 1 . Обчислити 
Вправи
138.Обчислити визначені інтеграли:
1)  2)
2)  3)
3) 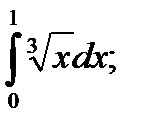
4) 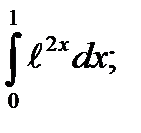 5)
5)  6)
6)  7)
7)  8)
8)  9)
9) 
10) 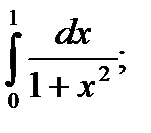 11)
11)  12)
12) 
13)  14)
14)  15)
15) 
16)  17)
17) 
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...