
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Размерность и базис векторного пространства
Определение. Вектор 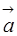 называется линейной комбинацией векторов
называется линейной комбинацией векторов  векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:
векторного пространства R, если он равен сумме произведений этих векторов на произвольные действительные числа:

| (8.1) |
где 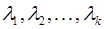 – какие угодно действительные числа.
– какие угодно действительные числа.
Определение. Векторы 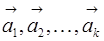 векторного пространства
векторного пространства  называются линейно зависимыми, если существуют, такие числа
называются линейно зависимыми, если существуют, такие числа 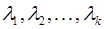 , не равные одновременно нулю, что:
, не равные одновременно нулю, что:
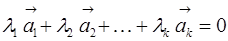
| (8.2) |
В противном случае векторы 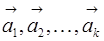 называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы 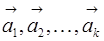 линейно независимы, если равенство
линейно независимы, если равенство 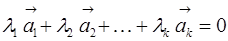 справедливо лишь при
справедливо лишь при 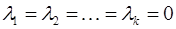 , и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 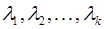 отлично от нуля.
отлично от нуля.
Можно показать, что если векторы 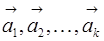 линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы. В противном случае векторы
линейно зависимы, то, по крайней мере, один из них линейно выражается через остальные. Верно и обратное утверждение о том, что если один из векторов выражается линейно через остальные, то все эти векторы в совокупности линейно зависимы. В противном случае векторы 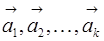 называются линейно независимыми.
называются линейно независимыми.
Из приведенных выше определений следует, что векторы 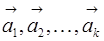 линейно независимы, если равенство (8.2) справедливо лишь при
линейно независимы, если равенство (8.2) справедливо лишь при 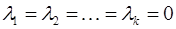 , и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел
, и линейно зависимы, если это равенство выполняется, когда хотя бы одно из чисел 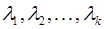 отлично от нуля.
отлично от нуля.
Примером линейно независимых векторов являются два неколлинеарных, т.е. не параллельных одной прямой, вектора 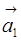 и
и 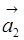 на плоскости. Действительно, условие (8.2)
на плоскости. Действительно, условие (8.2) 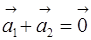 будет выполняться лишь в случае, когда
будет выполняться лишь в случае, когда 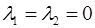 , ибо если, например,
, ибо если, например,  , то
, то  и векторы
и векторы 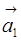 и
и 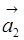 коллинеарны. Однако любые три вектора плоскости линейно зависимы.
коллинеарны. Однако любые три вектора плоскости линейно зависимы.
Отметим некоторые свойства векторов линейного пространства.
I.Если среди векторов 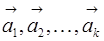 имеется нулевой вектор, то эти векторы линейно зависимы.
имеется нулевой вектор, то эти векторы линейно зависимы.
II.Если часть векторов 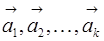 являются линейно зависимыми, то и все эти векторы — линейно зависимые.
являются линейно зависимыми, то и все эти векторы — линейно зависимые.
Определение. Линейное пространство  называется
называется  -мерным, если в нем существует
-мерным, если в нем существует  линейно независимых векторов, а любые из
линейно независимых векторов, а любые из 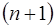 векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число
векторов уже являются зависимыми. Другими словами, размерность пространства — это максимальное число содержащихся в нем линейно независимых векторов. Число  называется размерностью пространства
называется размерностью пространства  и обозначается
и обозначается 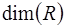 .
.
Определение.Совокупность  линейно независимых векторов
линейно независимых векторов  -мерного пространства
-мерного пространства  называется базисом.
называется базисом.
Справедлива следующая теорема.
Теорема. Каждый вектор 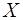 линейного пространства
линейного пространства  можно представить и притом единственным способом в виде линейной комбинации векторов базиса
можно представить и притом единственным способом в виде линейной комбинации векторов базиса 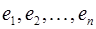 :
:

Это равенство называется разложением вектора 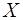 по базису
по базису 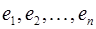 , а числа
, а числа 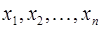 — координатами вектора
— координатами вектора 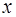 относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.
относительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.
Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, – противоположные по знаку координаты.
Теорема. Если 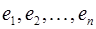 – система линейно независимых векторов пространства
– система линейно независимых векторов пространства  и любой вектор
и любой вектор 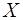 линейно выражается через
линейно выражается через 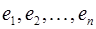 , то пространство
, то пространство  является
является  -мерным пространством
-мерным пространством  , а векторы
, а векторы 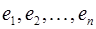 – его базисом.
– его базисом.
Базисом векторного пространства  называется любая независимая система линейно независимых
называется любая независимая система линейно независимых  –векторов этого пространства, количество которых равно
–векторов этого пространства, количество которых равно  , т.е. выбор системы базисных векторов векторного пространства
, т.е. выбор системы базисных векторов векторного пространства  неоднозначен, и может быть осуществлен большим числом способов.
неоднозначен, и может быть осуществлен большим числом способов.
Нередко приходится встречаться с заменой переменных, при которой старые переменные линейно выражаются через новые, например, при переходе от одного базиса пространства  к другому. Такую замену переменных называют обычно их линейным преобразованием.
к другому. Такую замену переменных называют обычно их линейным преобразованием.
Линейным преобразованием переменных называется выражение системы переменных 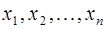 через новую систему переменных
через новую систему переменных  с помощью линейных однородных функций:
с помощью линейных однородных функций:
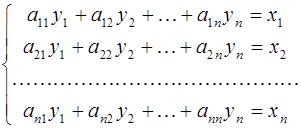
Линейное преобразование вполне определяется таблицей размером 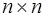 , составленной из коэффициентов при
, составленной из коэффициентов при  . Такая таблица, составленная из элементов
. Такая таблица, составленная из элементов 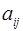 называется матрицей
называется матрицей  , а само преобразование представляет собой пример матричной операции. Понятие матрицы требует более детального рассмотрения, что и будет сделано в следующем разделе.
, а само преобразование представляет собой пример матричной операции. Понятие матрицы требует более детального рассмотрения, что и будет сделано в следующем разделе.
Контрольные вопросы к лекции №8
1. Понятие евклидова пространства.
2. Линейная зависимость и линейная независимость векторов.
3. Понятия размерности и базиса линейного пространства.
4. Линейное преобразование векторов.
Лекция 9. Матрицы
Основные понятия:
матрица; элемент матрицы; размер матрицы; строка; столбец; квадратная матрица; главная диагональ; побочная диагональ; диагональная матрица; скалярная матрица; единичная матрица; нулевая матрица; сумма матриц; произведение матриц; согласованные матрицы; транспонирование матриц; определитель матрицы; минор; алгебраическое дополнение; линейная зависимость; линейная комбинация; ранг матрицы; окаймляющий минор; элементарные преобразования матрицы; обратная матрица.
Основные понятия
Прямоугольная таблица:

| (9.1) |
состоящая из 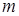 строк и
строк и  столбцов, называется матрицей размера
столбцов, называется матрицей размера 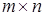 или
или  -матрицей.
-матрицей.
Матрицу (9.1) будем обозначать  или
или  . Числа
. Числа 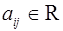 называются элементами матрицы, индекс
называются элементами матрицы, индекс  обозначает номер строки, а индекс
обозначает номер строки, а индекс  ‑ номер столбца, на пересечении которых расположен элемент.
‑ номер столбца, на пересечении которых расположен элемент.
Если 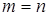 , то матрица (9.1) называется квадратной матрицей порядка
, то матрица (9.1) называется квадратной матрицей порядка  .
.
В квадратной матрице  -го порядка диагональ, состоящая из элементов
-го порядка диагональ, состоящая из элементов 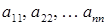 называется главной диагональю, состоящая из элементов
называется главной диагональю, состоящая из элементов 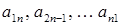 ‑ побочной диагональю.
‑ побочной диагональю.
Квадратная матрица:

называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. 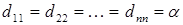 , то такая матрица называется скалярной. Скалярная матрица, у которой
, то такая матрица называется скалярной. Скалярная матрица, у которой 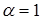 называется единичной и обозначается буквой
называется единичной и обозначается буквой 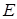 . Например, единичная матрица третьего порядка:
. Например, единичная матрица третьего порядка:
 .
.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.
Матрицы  и
и  называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
называются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.
Операции над матрицами
Суммой двух матриц 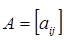 и
и 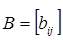 одинакового размера называется матрица
одинакового размера называется матрица  того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е.
того же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е. 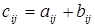 .
.
Сложение матриц обладает следующими свойствами:
1.Коммутативность, т.е.  .
.
2.Ассоциативность, т.е. 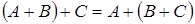 .
.
3.Для любых двух матриц  и
и  одинакового размера существует единственная матрица
одинакового размера существует единственная матрица 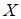 такая, что
такая, что 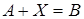 . Матрица
. Матрица 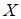 обозначается
обозначается 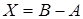 и называется разностью матриц
и называется разностью матриц  и
и  . Уравнение
. Уравнение  имеет решение
имеет решение 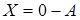 , получающаяся при этом матрица называется противоположной
, получающаяся при этом матрица называется противоположной  и обозначается
и обозначается 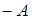 .
.
Произведением матрицы 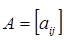 на число
на число 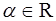 называется матрица, все элементы которой равны соответствующим элементам матрицы
называется матрица, все элементы которой равны соответствующим элементам матрицы  , умноженным на число
, умноженным на число 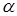 .
.
Умножение матрицы на действительное число обладает следующими свойствами:
1. 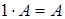 ;
;
2.  ;
;
3.  ;
;
4. 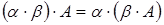 (ассоциативность);
(ассоциативность);
5. 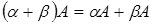 (дистрибутивность);
(дистрибутивность);
6. 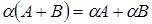 (дистрибутивность).
(дистрибутивность).
Матрица  называется согласованной с матрицей
называется согласованной с матрицей  , если число столбцов матрицы
, если число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  . В этом случае произведением матрицы
. В этом случае произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица 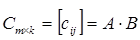 , где
, где 
 , т.е. элемент, стоящий в
, т.е. элемент, стоящий в  -той строке и
-той строке и  -том столбце матрицы произведения равен сумме произведений элементов
-том столбце матрицы произведения равен сумме произведений элементов  -той строки матрицы
-той строки матрицы  на соответствующие элементы
на соответствующие элементы  -го столбца матрицы
-го столбца матрицы  .
.
Свойства умножения:
1.Если матрица  согласована с матрицей
согласована с матрицей  , а матрица
, а матрица  согласована с матрицей
согласована с матрицей  , то
, то 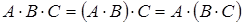 ‑ ассоциативность умножения;
‑ ассоциативность умножения;
2.  ‑ свойство дистрибутивности;
‑ свойство дистрибутивности;
3. Умножение матриц не коммутативно, т.е., как правило,  .
.
Транспонированием матрицы  называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е.
называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е.  -я строка матрицы
-я строка матрицы  становится
становится  -тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице
-тым столбцом транспонированной матрицы. Матрица, транспонированная к матрице  обозначается
обозначается 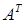 .
.
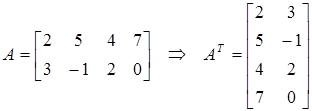
Свойства транспонирования:
1. 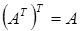
2. 
3. 
4. 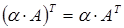
Определитель матрицы
Далее будем рассматривать только квадратные матрицы. Каждой квадратной матрице ставится в соответствие действительное число, называемое определителем матрицы и вычисляемое по определенному правилу.
Определитель матрицы естественно возникает при решении систем линейных уравнений, или в свернутой форме 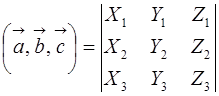 , или в свернутой форме
, или в свернутой форме  . Предыдущая формула получается разложением определителя по первой строке.
. Предыдущая формула получается разложением определителя по первой строке.
Возьмем теперь квадратную матрицу  -го порядка
-го порядка
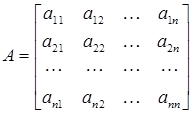
| (9.2) |
Для записи определителя  -го порядка матрицы
-го порядка матрицы  будем применять обозначения
будем применять обозначения 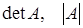 . При
. При  матрица
матрица  состоит из одного элемента и ее определитель равен этому элементу. При
состоит из одного элемента и ее определитель равен этому элементу. При 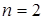 получаем определитель
получаем определитель 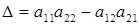 .
.
Минором 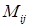 элемента
элемента  матрицы
матрицы  называют определитель матрицы
называют определитель матрицы  -го порядка, получаемого из матрицы
-го порядка, получаемого из матрицы  вычеркиванием
вычеркиванием  -той строки и
-той строки и  -го столбца.
-го столбца.
Пример 7. Найти минор 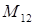 матрицы:
матрицы:
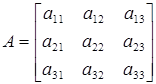 .
.
По определению, минор 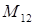 элемента
элемента 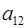 есть определитель матрицы, получаемой из матрицы
есть определитель матрицы, получаемой из матрицы  вычеркиванием первой строки и второго столбца. Следовательно,
вычеркиванием первой строки и второго столбца. Следовательно, 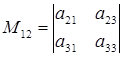 .
.
Алгебраическим дополнением элемента  матрицы
матрицы  называется минор
называется минор 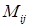 , взятый со знаком
, взятый со знаком 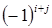 . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента  обозначается
обозначается  , следовательно,
, следовательно,  .
.
Пример 8. Найти алгебраическое дополнение элемента 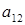 матрицы
матрицы  из примера 7.
из примера 7.
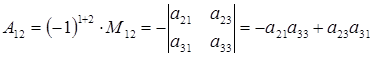 .
.
Определителем квадратной матрицы 
 -го порядка
-го порядка  называется число:
называется число:
 , ,
| (9.3) |
где  ‑ элементы первой строки матрицы (9.2), а
‑ элементы первой строки матрицы (9.2), а 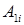 их алгебраические дополнения
их алгебраические дополнения 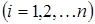 .
.
Запись по формуле (9.3) называется разложением определителя по первой строке.
Рассмотрим свойства определителей.
Свойство 1. При транспонировании матрицы ее определитель не меняется.
Это свойство устанавливает равноправность строк и столбцов определителя, поэтому определение определителя можно сформулировать так:
Определителем квадратной матрицы 
 -го порядка
-го порядка  называется число:
называется число:
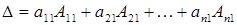 , ,
| (9.4) |
где 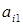 ‑ элементы первого столбца матрицы (9.2), а
‑ элементы первого столбца матрицы (9.2), а 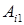 их алгебраические дополнения
их алгебраические дополнения 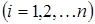 .
.
Свойство 2. Если поменять местами две строки или два столбца матрицы  , то ее определитель изменит знак на противоположный.
, то ее определитель изменит знак на противоположный.
Свойства 1 и 2 позволяют обобщить формулы (9.3) и (9.4) следующим образом:
Определитель квадратной матрицы  -го порядка (будем в дальнейшем говорить определитель
-го порядка (будем в дальнейшем говорить определитель  -го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
-го порядка) равен сумме попарных произведений любой строки (столбца) на их алгебраические дополнения.
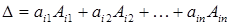 , или
, или 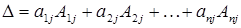 .
.
Свойство 3. Определитель, у которого две строки или два столбца одинаковы, равен нулю.
Действительно, поменяем в определителе  две одинаковые сроки местами. Тогда, по свойству 2 получим определитель
две одинаковые сроки местами. Тогда, по свойству 2 получим определитель  , но с другой стороны, определитель не изменится, т.е.
, но с другой стороны, определитель не изменится, т.е. 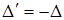 . Отсюда
. Отсюда 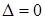 .
.
Свойство 4. Если все элементы какой-нибудь строки (столбца) определителя  умножить на число
умножить на число 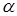 , то определитель умножится на
, то определитель умножится на 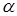 .
.
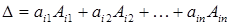 .
.
Умножим элементы  -той строки на
-той строки на 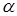 . Тогда получим определитель:
. Тогда получим определитель:
 .
.
Следствие 1. Если все элементы какой-нибудь строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.
Следствие 2. Если все элементы какой-нибудь строки (столбца) равны нулю, то определитель равен нулю.
Свойство 5. Определитель, у которого две строки (два столбца) пропорциональны, равен нулю.
Пусть  -я строка пропорциональна
-я строка пропорциональна  -ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
-ой строке. Вынося коэффициент пропорциональности за знак определителя, получим определитель с двумя одинаковыми строками, который по свойству 3 равен нулю.
Свойство 6. Если каждый элемент строки (столбца) определителя  есть сумма двух слагаемых, то определитель
есть сумма двух слагаемых, то определитель  равен сумме двух определителей: у одного из них
равен сумме двух определителей: у одного из них  -той строкой (столбцом)служат первые слагаемые, а у другого – вторые.
-той строкой (столбцом)служат первые слагаемые, а у другого – вторые.
Разложив определитель  по
по  -той строке получим:
-той строке получим:
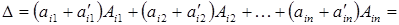
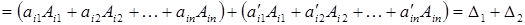 .
.
Свойство 7. Определитель не изменится, если к элементам какой-нибудь строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Прибавив к элементам  -той строки определителя
-той строки определителя  соответствующие элементы
соответствующие элементы  -ой строки, умноженные на число
-ой строки, умноженные на число 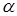 , получим определитель
, получим определитель 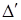 . Определитель
. Определитель 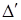 равен сумме двух определителей: первый есть
равен сумме двух определителей: первый есть  , а второй равен нулю, так как у него
, а второй равен нулю, так как у него  -тая и
-тая и  -тая строки пропорциональны.
-тая строки пропорциональны.
Свойство 8. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали, т.е.:
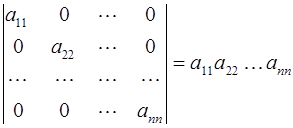
Свойство 9. Сумма произведений элементов какой-нибудь строки (столбца) определителя на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Рассмотрим вспомогательный определитель 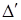 , который получается из данного определителя
, который получается из данного определителя  заменой
заменой  -той строки
-той строки  -той строкой. Определитель
-той строкой. Определитель 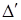 равен нулю, так как у него две одинаковые строки. Разложив его по
равен нулю, так как у него две одинаковые строки. Разложив его по  -той строке получим:
-той строке получим:
 .
.
Большое значение имеет следующий критерий равенства определителя нулю. Определитель квадратной матрицы равен нулю тогда и только тогда когда его строки (столбцы) линейно зависимы.
Строки (столбцы) матрицы называются линейно зависимыми, если одна (один) из них является линейной комбинацией с действительными коэффициентами остальных.
Теорема об определителе произведения двух квадратных матриц. Определитель произведения двух квадратных матриц равен произведению определителей этих квадратных матриц, т.е. 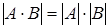 .
.
Ранг матрицы
Рангом матрицы называется наибольший порядок ее миноров, отличных от нуля. Ранг матрицы  обозначают
обозначают 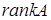 или
или 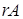 .
.
Если все миноры порядка 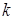 данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
данной матрицы равны нулю, то все миноры более высокого порядка данной матрицы также равны нулю. Это следует из определения определителя. Отсюда вытекает алгоритм нахождения ранга матрицы.
Если все миноры первого порядка (элементы матрицы  ) равны нулю, то
) равны нулю, то  . Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то
. Если хотя бы один из миноров первого порядка отличен от нуля, а все миноры второго порядка равны нулю, то 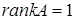 . Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка
. Причем, достаточно просмотреть только те миноры второго порядка, которые окаймляют ненулевой минор первого порядка. Если найдется минор второго порядка отличный от нуля, исследуют миноры третьего порядка, окаймляющие ненулевой минор второго порядка. Так продолжают до тех пор, пока не придут к одному из двух случаев: либо все миноры порядка 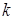 , окаймляющие ненулевой минор
, окаймляющие ненулевой минор 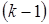 -го порядка равны нулю, либо таких миноров нет. Тогда
-го порядка равны нулю, либо таких миноров нет. Тогда  .
.
Пример 10. Вычислить ранг матрицы 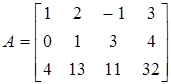 .
.
Минор первого порядка (элемент 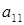 ) отличен от нуля. Окаймляющий его минор
) отличен от нуля. Окаймляющий его минор 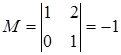 тоже не равен нулю.
тоже не равен нулю.
Далее рассмотрим миноры, окаймляющие минор 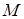 :
:
 ;
;
 .
.
Все эти миноры равны нулю, значит  .
.
Приведенный алгоритм нахождения ранга матрицы не всегда удобен, поскольку связан с вычислением большого числа определителей. Наиболее удобно пользоваться при вычислении ранга матрицы элементарными преобразованиями, при помощи которых матрица приводится к столь простому виду, что очевидно, чему равен ее ранг.
Элементарными преобразованиями матрицы называют следующие преобразования:
Ø умножение какой-нибудь строки (столбца) матрица на число, отличное от нуля;
Ø прибавление к одной строке (столбцу) другой строки (столбца), умноженной на произвольное число.
Полужордановым преобразованием строк матрицы:

с разрешающим элементом 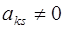 называется следующая совокупность преобразований со строками матрицы:
называется следующая совокупность преобразований со строками матрицы:
Ø к первой строке прибавить 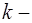 ю, умноженную на число
ю, умноженную на число 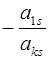 и т.д.;
и т.д.;
Ø к последней строке прибавить 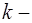 ю, умноженную на число
ю, умноженную на число 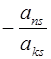 .
.
После выполнения этих преобразований получается матрица:
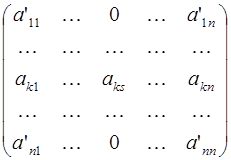
Полужордановым преобразованием столбцов матрицы с разрешающим элементом 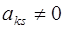 называется следующая совокупность преобразований со столбцами матрицы:
называется следующая совокупность преобразований со столбцами матрицы:
Ø к первму столбцу прибавить 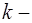 й, умноженный на число
й, умноженный на число 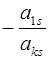 и т.д.;
и т.д.;
Ø к последнему столбцу прибавить 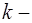 й, умноженный на число
й, умноженный на число 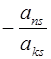 .
.
После выполнения этих преобразований получается матрица:
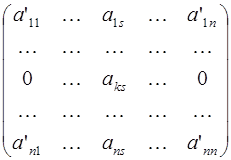
Полужорданово преобразование строк или столбцов квадратной матрицы не изменяет ее определителя.
Элементарные преобразования матрицы не изменяют ее ранга. Покажем на пример, как вычислить ранг матрицы, пользуясь элементарными преобразованиями.
Пример 11. Вычислить ранг матрицы 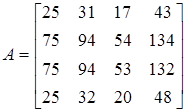 .
.
Применим к матрице  элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.
элементарные преобразования: первую строку матрицы, умноженную на (-3) прибавим ко второй и третьей и ее же вычтем из последней.

Вычитая далее вторую строку из третьей и последней, имеем:
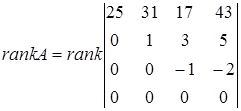 .
.
Последняя матрица содержит отличный от нуля минор  третьего порядка, определитель же самой матрицы
третьего порядка, определитель же самой матрицы  равен нулю. Следовательно,
равен нулю. Следовательно,  .
.
Отметим два важных свойства ранга матрицы:
· Ранг матрицы не меняется при ее транспонировании;
· Если ранг матрицы равен 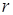 , то любые ее
, то любые ее 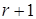 строк (столбцов) линейно зависимы.
строк (столбцов) линейно зависимы.
Обратная матрица
Пусть  - квадратная матрица порядка
- квадратная матрица порядка  . Матрица
. Матрица  называется обратной матицей к матрице
называется обратной матицей к матрице  , если выполняются равенства
, если выполняются равенства  , где
, где 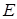 ‑ единичная матрица порядка
‑ единичная матрица порядка  .
.
Теорема 1. Если для данной матрицы существует обратная матрица, то она единственная.
Пусть 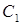 и
и 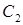 ‑ матрицы, обратные к матрице
‑ матрицы, обратные к матрице  . Тогда
. Тогда 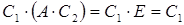 , с другой стороны,
, с другой стороны,  .
.
Откуда 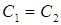 . Обратную матрицу к матрице
. Обратную матрицу к матрице  обозначают
обозначают 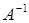 .
.
Теорема 2. Матрица  имеет обратную матрицу тогда и только тогда, когда
имеет обратную матрицу тогда и только тогда, когда  .
.
Пусть  имеет обратную матрицу. Тогда
имеет обратную матрицу. Тогда 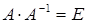 и, применяя теорему об умножении определителей, получаем
и, применяя теорему об умножении определителей, получаем 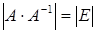 или
или 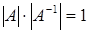 . Следовательно,
. Следовательно,  .
.
Пусть  . Укажем явное выражение матрицы
. Укажем явное выражение матрицы 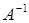 через элементы матрицы
через элементы матрицы  , а именно: если
, а именно: если 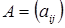 , то:
, то:
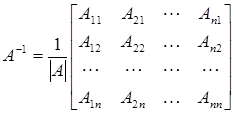 , ,
| (9.5) |
здесь  ‑ алгебраическое дополнение к элементу
‑ алгебраическое дополнение к элементу  . Матрица (9.5) получается из матрицы
. Матрица (9.5) получается из матрицы  следующим образом. Сначала вместо каждого элемента
следующим образом. Сначала вместо каждого элемента  пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную
пишется его алгебраическое дополнение, затем полученная матрица транспонируется и получается т.н. присоединенная матрица. Для получения обратной матрицы присоединенная матрица умножается на величину, обратную 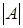 .
.
Непосредственное умножение  на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к
на матрицу (9.5) слева и справа дает единичную матрицу, что подтверждает, что (9.5) – матрица, обратная к  .
.
Пример 12. Найти обратную матрицу к матрице 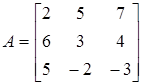 .
.
Так как  , то
, то 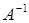 существует. Вычислим алгебраические дополнения элементов матрицы
существует. Вычислим алгебраические дополнения элементов матрицы  :
:
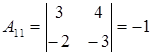 , ,
|  , ,
|
 , ,
|  , ,
|
 , ,
| 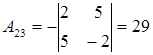 , ,
|
 , ,
| 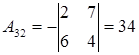 , ,
|
 . .
|
Матрицу 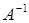 находим в два приема, согласно формуле (9.5). Сначала запишем матрицу
находим в два приема, согласно формуле (9.5). Сначала запишем матрицу  , состоящую из алгебраических дополнений элементов
, состоящую из алгебраических дополнений элементов  .
.  Затем матрица
Затем матрица  транспонируется и умножается на число обратное
транспонируется и умножается на число обратное 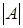 , в данном случае – на (-1). Окончательно получаем:
, в данном случае – на (-1). Окончательно получаем:
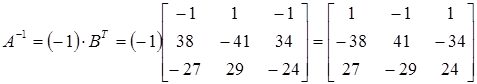 .
.
Матрица называется неособенной или невырожденной, если ее определитель не равен нулю. Отметим свойства обратных матриц. Если  и
и  ‑ невырожденные матрицы одинакового порядка, то:
‑ невырожденные матрицы одинакового порядка, то:
 ,
,
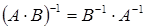 ,
,
 ,
,
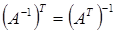 .
.
Контрольные вопросы к лекции №9
1. Понятие матрицы.
2. Виды матриц.
3. Понятие транспонирования матриц.
4. Операции сложения и вычитания матриц.
5. Операции умножения и возведения в степень матриц.
6. Понятие определителя.
7. Определитель 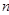 - го порядка.
- го порядка.
8. Правила нахождения определителей 2 и 3 порядка.
9. Свойства определителей.
10. Правила нахождения определителей 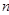 - го порядка.
- го порядка.
11. Понятие обратной матрицы.
12. Схема нахождения обратной матрицы.
13. Понятие ранга матрицы.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...