
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Числовое и геометрическое представление ФАЛ
Часто для упрощения записи ФАЛ вместо полного перечисления термов используют номера наборов, для которых функция = 1. Например  , то есть на 0, 3 и 4-м наборах функция = 1. Такая форма записи называется числовой.
, то есть на 0, 3 и 4-м наборах функция = 1. Такая форма записи называется числовой.
 ФАЛ имеют и геометрическое представление, так функция 2-х переменных рассматривают как плоскость, заданную в системе координат
ФАЛ имеют и геометрическое представление, так функция 2-х переменных рассматривают как плоскость, заданную в системе координат  . Отложим по каждой оси единичные отрезки
. Отложим по каждой оси единичные отрезки 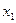 и
и 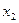 . Получим квадрат, вершины которого – комбинации переменных.
. Получим квадрат, вершины которого – комбинации переменных.
Две вершины, принадлежащие одному ребру “склеиваются” по переменной меняющейся вдоль ребра.
Для функции 3-х переменных геометрическое представление выполняются в виде куба, вершины которого обозначены десятичными цифрами, двоичными цифрами и произвольными переменными  . Рёбра куба поглощают вершины. Грани куба поглощают свои рёбра и, следовательно, вершины.
. Рёбра куба поглощают вершины. Грани куба поглощают свои рёбра и, следовательно, вершины.
Терм максимального ранга называют 0-кубом (точкой) и обозначают  .
.
Пусть 

Если два 0-куба из  различаются только по одной координате, то они образуют 1-куб (отрезок):
различаются только по одной координате, то они образуют 1-куб (отрезок):  , где х – независимая координата.
, где х – независимая координата.
Если два 1-куба различны только по одной координате, то они образуют 2-куб (грань).
Трёхмерный куб получается при соединении соответствующих вершин двух двумерных кубов отрезками единичной длины.
 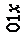    |

Глава 8
Минимизация функций алгебры логики
Общая задача минимизации булевых функций может быть сформулирована таким образом: найти аналитическое выражение заданной булевой функции в форме, содержащей минимальное число букв. Эта задача достаточно хорошо исследована в классе дизъюнктивно – конъюнктивных форм.
Определение: Минимальной ДНФ булевой функции называется ДНФ, содержащая наименьшее число букв по отношению к другим ДНФ, представляющим заданную булеву функцию.
Определение: Булева функция q(x1… xn) называется импликантой булевой функции f(x1… xn) если для любого набора переменных, на котором  , справедливо
, справедливо  .
.
Определение: Импликанта  булевой функции
булевой функции 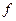 , являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты
, являющаяся элементарной конъюнкцией, называется простой, если никакая часть импликанты  не является импликантой функции
не является импликантой функции 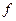 .
.
1. Дизъюнкция любого числа импликант булевой функции 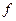 так же является импликантой этой функции.
так же является импликантой этой функции.
2. Любая булева функция 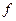 эквивалентна дизъюнкции всех своих простых импликант. Такая форма называется сокращенной ДНФ.
эквивалентна дизъюнкции всех своих простых импликант. Такая форма называется сокращенной ДНФ.
Пример:
| x1 | x2 | x3 | f | q1 | q2 | q3 | q4 | q5 | q6 | q7 |


 и
и  простые импликанты.
простые импликанты.
Сокращенная ДНФ  :
:
Импликанты  и
и  покрывают своими "1" все "1" функции
покрывают своими "1" все "1" функции 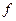 .
.
Получение сокращенной ДНФ является первым этапом отыскания минимальных форм булевых функций. Иногда из СкДНФ можно убрать одну или несколько простых импликант, не нарушая эквивалентности исходной функции. Такие простые импликанты называются лишними. Их исключение из СкДНФ – второй этап минимизации.
Определение: СкДНФ булевой функции называется тупиковой, если в ней отсутствуют лишние простые импликанты.
Тупиковые ДНФ булевых функций 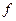 , содержащие минимальное число букв, являются минимальными. МДНФ может быть несколько.
, содержащие минимальное число букв, являются минимальными. МДНФ может быть несколько.
Метод Квайна
Метод применим к СДНФ и основывается на применении двух основных соотношений:
1. склеивание 
2. поглощение 
Суть метода заключается в последовательном выполнении всех возможных склеиваний и затем всех поглощений, что приводит к СкДНФ.
Для получения МДНФ необходимо убрать из СкДНФ все лишние простые импликанты с помощью импликантной матрицы Квайна. В строках матрицы отмечаются простые импликанты, а в столбцах – конституэнты "1" булевой функции. Минимальные ДНФ строятся по импликантной матрице таким образом:
1) ищутся столбцы матрицы, имеющие только один крестик. Соответствующие этим крестикам простые импликанты называются базисными и составляют ядро булевой функции. Ядро обязательно входит в МДНФ.
2) рассматриваются различные варианты выбора совокупности простых импликант, которые накроют крестиками остальные столбцы матрицы, и выбираются варианты с минимальным суммарным числом букв в такой совокупности импликант.
Пример:  .
.
1) Избавимся от отрицаний и скобок: 
2) Восстановим СДНФ, применяя развертывание:

3) Найдем СкДНФ, произведя все возможные склеивания:

4) Ищем МДНФ:
 |
Ядро: 
МДНФ: 

Метод Квайна-Мак-Класки
Метод формализован на этапе нахождения простых импликант. Формализация проводится таким образом:
1) Все конституэнты "1" из СДНФ булевой функции 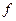 записываются их двоичными номерами.
записываются их двоичными номерами.
2) Все номера разбиваются на непересекающиеся группы, в i-ой группе находятся конституэнты "1", содержащие i единиц в номере.
3) Склеиваются только номера соседних групп, склеивание номера как-либо отмечают.
4) Производят все возможные склеивания. Неотмеченные после склеивания номера являются простыми импликантами.
Пример:

1) В СДНФ заменим все конституэнты "1" их двоичными номерами:

2) Образуем группы двоичных номеров и произведем склеивание:
| номер группы | двоичные номера конституэнт "1" | номер группы | двоичные номера конституэнт "1" | номер группы | двоичные номера конституэнт "1" | ||
| -
| | 0**1 |

Простые импликанты: *111, 111*, 0**1
МДНФ: 
Разбиение конституэнт на группы позволяет уменьшить число парных сравнений при склеивании.
Метод Нельсона
Метод позволяет получить СкДНФ булевой функции 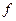 из ее произвольной КНФ. Если в произвольной КНФ булевой функции
из ее произвольной КНФ. Если в произвольной КНФ булевой функции 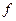 раскрыть все скобки и произвести все поглощения, то в результате будет получена СкДНФ булевой функции
раскрыть все скобки и произвести все поглощения, то в результате будет получена СкДНФ булевой функции 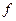 .
.
Пример: 
Найдем СкДНФ: 
Произведем поглощения:  - СкДНФ.
- СкДНФ.
Метод диаграмм Вейча
Метод получает МДНФ булевой функции небольшого числа переменных. Булевы функции задаются в виде специальных диаграмм. Для функции 2-х переменных и 3-х переменных:

Добавление к диаграмме 3-х переменных еще такой же даст диаграмму 4-х переменных, если приписать еще одну диаграмму 4-х переменных, то получим диаграмму для функции 5-ти переменных.
Правила склеивания конституэнт "1" на диаграммах Вейча: склеиванию подлежат прямоугольные конфигурации, заполненные конституэнтами "1" и содержащие число клеток, являющееся степенью 2. Получающееся новое элементарное произведение определяется как произведение переменных, не меняющих своего значения на всех склеиваемых наборах. Минимизация булевой функции заключается в нахождении минимального накрытия всех единиц диаграммы Вейча блоками из единиц, расположенных в соседних клетках диаграммы.
Примеры: Булевы функции заданы диаграммами Вейча. Найти их МДНФ.
 |

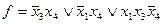

Метод самопонижающихся циклов
 Метод самопонижающихся циклов позволяет получить СкДНФ булевой функции по специальным фрагментам ее таблицы истинности. Каждый фрагмент выделяется так, что может описываться только одной конъюнкцией. СкДНФ получается путем логического сложения конъюнкций, соответствующих фрагментам, при условии, что все выделенные фрагменты таблицы истинности булевой функции полностью покрывают ту ее часть, где булева функция =1.
Метод самопонижающихся циклов позволяет получить СкДНФ булевой функции по специальным фрагментам ее таблицы истинности. Каждый фрагмент выделяется так, что может описываться только одной конъюнкцией. СкДНФ получается путем логического сложения конъюнкций, соответствующих фрагментам, при условии, что все выделенные фрагменты таблицы истинности булевой функции полностью покрывают ту ее часть, где булева функция =1.
Если в таблице истинности произвольной булевой функции 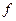 существует фрагмент вида (см. таблицу), то ее СкДНФ на этом фрагменте описывается выражением
существует фрагмент вида (см. таблицу), то ее СкДНФ на этом фрагменте описывается выражением 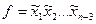 , так как по переменным
, так как по переменным  может быть произведено полное склеивание. Никаких ограничений на число склеенных переменных и размещение их во фрагменте таблицы истинности булевой функции не накладывается. Если имеется фрагмент, содержащий
может быть произведено полное склеивание. Никаких ограничений на число склеенных переменных и размещение их во фрагменте таблицы истинности булевой функции не накладывается. Если имеется фрагмент, содержащий  двоичных наборов длины n, где m – число склеенных переменных, то такой фрагмент описывается конъюнкцией ранга (n-m) в представлении булевой функции
двоичных наборов длины n, где m – число склеенных переменных, то такой фрагмент описывается конъюнкцией ранга (n-m) в представлении булевой функции 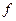 СкДНФ по этому фрагменту. Фрагмент вида (см. таблицу) называется самопонижающимся циклом, а число склеенных переменных во фрагменте – рангом самопонижающегося цикла.
СкДНФ по этому фрагменту. Фрагмент вида (см. таблицу) называется самопонижающимся циклом, а число склеенных переменных во фрагменте – рангом самопонижающегося цикла.
Пример:
Найти СкДНФ булевой функции 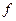 методом самопонижающихся циклов. Функция
методом самопонижающихся циклов. Функция 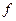 задана таблицей истинности.
задана таблицей истинности.

1. 
Ищем циклы максимального ранга  . Имеется только один такой цикл №1
. Имеется только один такой цикл №1  . Найденный цикл покрывает не все "1" таблицы истинности функции
. Найденный цикл покрывает не все "1" таблицы истинности функции 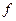 .
.
2. Ищем циклы ранга  . Имеется два таких цикла №2 и №3. Цикл №3 полностью содержится в цикле №1, поэтому цикл №3 не рассматривается. Поиск цикла меньшего ранга не нужен, так как циклы 1 и 2 полностью покрывают конституэнты "1" функции
. Имеется два таких цикла №2 и №3. Цикл №3 полностью содержится в цикле №1, поэтому цикл №3 не рассматривается. Поиск цикла меньшего ранга не нужен, так как циклы 1 и 2 полностью покрывают конституэнты "1" функции 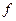 .
.
СкДНФ: 
Минимизация монотонных функций
Для монотонных функций СкДНФ совпадает с минимальной, что следует из теоремы: для того, чтобы булева функция Ж была монотонной, необходимо и достаточно, чтобы ее СкДНФ не содержала отрицаний переменных. СкДНФ является и МДНФ булевой функции.
Для получения МДНФ монотонных функций могут быть использованы все методы нахождения СкДНФ произвольных булевых функций.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...