
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Проверка гипотезы о виде распределения генеральной совокупности по критерию Колмогорова-Смирнова
Пусть эмпирическое распределение задано интервальным статистическим рядом
| Интервал | х 1 – х 2 | х 2 – х 3 | … | х i–1 – х i | … | х m –1 – х m |
| ni | n 1 | n 2 | … | n i | … | n m |
Объем выборки равен n = n 1+ n 2+…+ n m .
Требуется при заданном уровне значимости a проверить, подчиняется ли генеральная совокупность выбранному теоретическому закону распределения f(x).
Выдвинем гипотезы
Н0: Признак Х подчиняется закону распределения f(x)
Н1: Признак Х не подчиняется закону распределения f(x)
Для проверки сформулированных гипотез при помощи критерия Колмогорова-Смирнова необходимо выполнить ряд расчетов.
а) Определяют по выборке параметры выбранного теоретического распределения f(x). Пусть r - число параметров распределения.
б) Для каждого интервала Х определяют вероятности попадания признака Х в данный интервал. Для этого нужно использовать формулу из теории вероятности
 .
.
Здесь f(x) – дифференциальная функция распределения, F(x) – интегральная функция распределения. Для многих видов распределения имеются таблицы значений f(x) и F(x).
в) Определяют теоретические частоты
 .
.
г) Находят накопленные частоты: для эмпирических частот – n×Fn(x) ; для теоретических частот – n×F(x). Для этого следует для каждого интервала последовательно складывать частоты, начиная с первого интервала и заканчивая текущим интервалом. Результаты расчетов удобно записать в таблицу.
д) Далее вычисляют модуль разности накопленных частот в каждом интервале ôn×Fn(x) – n×F(x)ô = n×ôFn(x) – ×F(x)ô.
е) Находят наибольший из полученных модулей
n ×D = max{n×ôFn(x) – ×F(x)ô}.
ж) Определяют наблюдаемое значение критерия согласия Колмогорова
 .
.
Этот критерий является случайной величиной, которая подчиняется закону распределения Колмогорова.
з) По таблице критических точек (приложение 8), используя заданный уровень значимости a находят критическое значение критерия lкр = l(a).
е) Если в результате сравнения окажется lнабл < lкр, то нет оснований отвергнуть нулевую гипотезу H0; если же lнабл > lкр, то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Замечание: в критерии Колмогорова рекомендуется брать более “жесткий” уровень значимости a ³ 0,1.
Примеры
Пример 1.
Предполагается, что применение новой технологии в разработке пластовых месторождений приведет к увеличению качества угля. Результаты контроля по качеству добытого угля двумя бригадами, работающими в аналогичных условиях, но использующими разные технологии, приведены ниже. Замеры велись по проценту засорения угля, вырабатываемого одной бригадой за смену по старой технологии (признак Х1) и новой технологии (признак Х2).
Х1 (в %): 13; 10,5; 11; 12; 20; 18,8; 10
Х2 (в %): 6; 13; 21; 7; 9; 9; 5; 10
Подтверждают ли эти результаты предположение об эффективности применения новой технологии? Принять a = 0,01 .
Предположить, что выборки получены из нормально распределенных генеральных совокупностей.
Проведем первичную обработку статистических данных, используя формулы для несгруппированного ряда данных (раздел 2.2, случай а).
Получим по признаку Х1 : объем выборки n=7;
Выборочная средняя  (13+10,5+11+12+20+18,8+10)/7= 13,61
(13+10,5+11+12+20+18,8+10)/7= 13,61
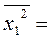 (132+10,52+112+122+202+18,82+102)/7= 199,67
(132+10,52+112+122+202+18,82+102)/7= 199,67
Выборочная дисперсия Dв = 199,67 –13,612 = 14,44
Исправленная СКО S2x1 =14,44×7/6 = 16,84
Параметры признака Х2 рассчитываются аналогично:
n=8;  10;
10;  116,625 ;
116,625 ;
Dв = 116,625 – 102 = 16,625 : S2x2 =16,625×8/7 = 19 .
Вопрос эффективности применения новой технологии сводится к проверке статистической гипотезе о равенстве двух средних (математических ожиданий) генеральных совокупностей. Для корректного решения необходимо убедиться в равенстве дисперсий указанных генеральных совокупностей (п. 2.4.1).
Выдвинем основную и альтернативную гипотезы.
Н0: D(Х2) = D(Х1)
Н1: D(Х2) > D(Х1)
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия (отношение большей дисперсии к меньшей):

Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)
при a =0,01; k1 = 8 –1 = 7; k2 = 7 –1 = 6
Fкр=F(0,01;7;6) = 8,26
В результате сравнения получим Fнабл < Fкр. Значит, нет оснований отвергнуть нулевую гипотезу H0. Следовательно, принимаем гипотезу о равенстве дисперсий двух генеральных совокупностей.
Для выяснения эффективности применения новой технологии проверим статистическую гипотезу о равенстве двух средних генеральных совокупностей (п. 2.4.2).
Выдвинем основную и альтернативную гипотезы.
Н0: M(Х1) = M(Х2)
Н1: M(Х1) > M(Х1)
Принятие нулевой гипотезы Н0 даст основания считать, что новая система технологии добычи угля не приводит к изменению засорения угля.
Принятие гипотезы H1 будет значить, что новая система технологии приводит к уменьшению засорения угля, и, следовательно, она эффективна.
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия

Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с k =7+8–2=13 степенями свободы.
Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область)
tкр = t(0,01;13) = 2,65.
В результате сравнения получим Tнабл < tкр . Значит, нет оснований отвергнуть нулевую гипотезу H0. Следовательно, новая система технологии не приводит к изменению качества угля по засорению. Она не эффективна.
Пример 2
При уровне значимости a=0,05 проверить гипотезу о нормальном законе распределения генеральной совокупности признака У из задачи 1 (п. 2.3) , используя критерий Пирсона.
Проверим гипотезу о нормальном распределении признака Y. Используем критерий Пирсона.
Нормальный закон распределения является двухпараметрическим распределением с параметрами а и s. Значит, r = 2. Из выборки по У возьмем оценки параметров распределения:
а »  =7,284; s » S у = 2,254 .
=7,284; s » S у = 2,254 .
Для каждого интервала признака У необходимо вычислить вероятности попадания признака в данный интервал. Используем готовую формулу из теории вероятности для величины, распределенной нормально:
 .
.
Здесь используются нормированная нормальная случайная величина  . Функция Лапласа Ф(z )вычисляется по таблице (приложение 2). При этом учитываем, что
. Функция Лапласа Ф(z )вычисляется по таблице (приложение 2). При этом учитываем, что
Ф(–z) = – Ф(z); Ф(– ¥) = –0,5 ; Ф(+ ¥) = 0,5 .
В данном случае вместо случайной величины Х берем случайную величину У. Далее заполним таблицу по формулам: 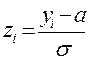 ;
; 
причем крайнюю левую точку интервала заменяем на – ¥ ; крайнюю правую точку заменяем на + ¥, поскольку теоретическое нормальное распределение определено на всей числовой оси.
Теоретические частоты найдем по формуле:

где функция Лапласа Ф(z)вычисляется по таблице (приложение 2). При этом учитываем, что Ф(–z) = – Ф(z); Ф(– ¥) = –0,5 ; Ф(+ ¥) = 0,5 .
Получим таблицу:
| Уi | Уi+1 | ni | zi | zi+1 | Ф(zi) | Ф(zi+1) | ni* | Ni* | Ni | Вi | Vi |
| 3,2 | 4,68 | – ¥ | -1,16 | -0,5 | -0,377 | 6,15 | 6,15 | 0,21504 | 4,06504 | ||
| 4,68 | 6,16 | -1,16 | -0,50 | -0,377 | -0,1915 | 9,28 | 9,28 | 0,80061 | 15,5256 | ||
| 6,16 | 7,64 | -0,50 | 0,16 | -0,1915 | 0,0636 | 12,76 | 12,76 | 0,12152 | 15,3665 | ||
| 7,64 | 9,12 | 0,16 | 0,81 | 0,0636 | 0,291 | 11,37 | 11,37 | 0,16507 | 8,79507 | ||
| 9,12 | 10,6 | 0,81 | 1,47 | 0,291 | 0,4292 | 6,91 | 10,45 | 0,2012 | 7,7512 | ||
| 10,6 | 12,08 | 1,47 | 2,13 | 0,4292 | 0,4834 | 2,71 | |||||
| 12,08 | 13,56 | 2,13 | + ¥ | 0,4834 | 0,5 | 0,83 | |||||
| Итого | 1,50344 | 51,5034 |
После заполнения 8–го столбца отмечаем, что два последних элемента в этом столбце меньше пяти. Поскольку в критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты трех последних интервалов Ni* – для 8–го столбца; Ni – для 3–го столбца.
11–ый столбец заполняем по формуле: Вi = 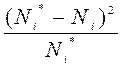 .
.
12–ый столбец – контрольный. Он вычисляется по формуле:
Vi = 
Сделаем проверку: 50 + 1,5034 = 51, 5034. Верно.
Заметим, что в результате проверки значения правой и левой частей могут отличатся незначительным образом.
Запишем наблюдаемое значение критерия: c2набл = 1,5034.
Выберем уровень значимости ошибки a=0,05.
Число степеней свободы равно k=m –2 – 1 , где m – число интервалов после объединения. В нашем случае число интервалов после объединения m= 5. Тогда число степеней свободы равно k=5–3 = 2. По таблице критических точек c2 (Приложение 5) находим c2кр(0,05; 2)=6.
Сравниваем: c2набл < c2кр .
Следовательно, нет оснований отвергнуть гипотезу о нормальном законе распределения признака Y . Поэтому принимается гипотеза о нормальном распределении признака У.
Пример 3. В результате опыта получены данные по времени безотказной работы стопора путевого ( в часах).
При уровне значимости a=0,2 при помощи критерия Колмогорова-Смирнова проверить гипотезу о показательном законе распределения генеральной совокупности по времени безотказной работы стопора.
Для признака Х (времени безотказной работы стопора ) определим наибольшее и наименьшее значение признака:
Xmin=106 ; Xmax=1246 ; объем выборки n = 40.
Число интервалов разбиения определим по формуле Стэрджесса:
k =1 + 3,322× lg 40 = 6,3 .
Найдем шаг разбиения h = (Хmax – Xmin) / k.
В данном случае h = (1246 –106) / 6,3 = 180,32. Примем h = 200.
Произведем группировку данных для признака Х.
Результаты группировки представим в таблице, с помощью которой рассчитаем параметры выборки по методу “условного нуля”.
| i | интервалы | хi | ni | ui | ni× ui | ni× ui2 | ni× (ui + 1)2 |
| 100-300 | -2 | -48 | |||||
| 300-500 | -1 | -6 | |||||
| 500-700 | |||||||
| 700-900 | |||||||
| 900-1100 | |||||||
| 1100-1300 | |||||||
| S | -44 |
Условный нуль : С=600.
Проверка: 74 = 122 + 2·(–44) + 40 – верно.
Из таблицы находим условные моменты:
М1 = -44/40 = –1,1; М2 = 122/40 = 3,05.
Выборочная средняя равна:
 =М1·h +C = 380.
=М1·h +C = 380.
Выборочная дисперсия равна:
Dв = [M2 - (M1)2]·h2 = 73600
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...