
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Принципы традиционного динамического программирования
Динамическое программирование (иначе “динамическое планирование”) есть особый метод оптимизации решений, специально приспособленный к так называемым “многошаговым” (или “многоэтапным”) операциям. Теоретические основы этого метода рассмотрены в [2], в [ 3 ] на стр. 245 – 265, и в [ 4 ] на стр. 142 – 150, оттуда же взяты соответствующие примеры.
Представим себе некоторую операцию Q, распадающуюся на ряд последовательных “шагов” или “этапов”, например деятельность отрасли промышленности в течение ряда лет; или же преодоление группой самолетов нескольких полос противовоздушной обороны; или же последовательность шагов, применяемых при контроле аппаратуры. Некоторые операции (подобно вышеприведенным) расчленяются на шаги естественно; в некоторых членение приходится вводить искусственно: например, процесс наведения ракеты на цель можно и нужно разбить на этапы, каждый из которых занимает какое-то время.
Рассмотрим операцию Q, состоящую из т шагов (этапов). Пусть эффективность операции характеризуется каким-то показателем W,который мы для краткости будем именовать “выигрышем”. Предположим, что выигрыш Wзавсю операцию складывается из выигрышей на отдельных шагах:

где wi – выигрыш на i-м шаге.
Если W обладает таким свойством, то его называют аддитивным критерием.
Любую многошаговую задачу можно решать по-разному: либо искать сразу все элементы решения на всех т шагах, либо же строить оптимальное управление шаг за шагом, на каждом этапе расчета оптимизируя только один шаг. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов. При использовании компьютерных сервисов первый способ оказывается выгоднее, и в дальнейшем мы будем его применять, но вначале ознакомимся с традиционным динамическим программированием.
В основе метода динамического программирования лежит идея постепенной, пошаговой оптимизации. Оптимизация одного шага, как правило, проще оптимизации всего процесса: лучше, оказывается, много раз решить сравнительно простую задачу, чем один раз – сложную.
С первого взгляда идея может показаться довольно тривиальной. В самом деле, чего, казалось бы, проще: если трудно оптимизировать операцию в целом, разбить ее на ряд шагов. Каждый такой шаг будет отдельной маленькой операцией, оптимизировать которую уже нетрудно. Надо выбрать на этом шаге такое управление, чтобы эффективность этого шага была максимальна. Не так ли? Нет, вовсе не так. Принцип динамического программирования отнюдь не предполагает, что каждый шаг оптимизируется отдельно, независимо от других. Напротив, шаговое управление должно выбираться дальновидно, с учетом всех его последствий в будущем. Что толку, если мы выберем на данном шаге управление, при котором эффективность этого шага максимальна, если этот шаг лишит нас возможности хорошо выиграть на последующих шагах?
Пусть, например, планируется работа группы промышленных предприятий, из которых часть занята выпуском предметов потребления, а остальные производят для них машины. Задача операции — получить за т лет максимальный объем выпуска предметов потребления. Допустим, планируются капиталовложения на первый год. Исходя из узких интересов этого шага (года), мы должны были бы все наличные средства вложить в производство предметов потребления. Но правильно ли будет такое решение с точки зрения эффективности операции в целом? Очевидно, нет. Это решение – расточительное, недальновидное. Имея в виду будущее, надо выделить какую-то долю средств и на производство машин. От этого объем продукции за первый год, конечно, снизится, зато будут созданы условия для его увеличения в последующие годы.
Еще пример. Допустим, что в задаче прокладки железнодорожного пути из А в В мы прельстимся идеей сразу же устремиться по самому легкому (дешевому) направлению. Что толку от экономии на первом шаге, если в дальнейшем он заведет нас (буквально или фигурально) в «болото»?
Значит, планируя многошаговую операцию, надо выбирать управление на каждом шаге с учетом всех его будущих последствий на еще предстоящих шагах. Управление на i-м шаге выбирается не так, чтобы выигрыш именно на данном шаге был максимален, а так, чтобы была максимальна сумма выигрышей н а всех оставшихся до конца шагах плюс данный.
Однако из этого правила есть исключение. Среди всех шагов есть один, который может планироваться попросту, без оглядки на будущее. Какой это шаг? Очевидно, последний! Этот шаг, единственный из всех, можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.
Поэтому процесс динамического программирования обычно разворачивается от конца к началу: прежде всего планируется последний, m-й шаг. А как его спланировать, если мы не знаем, чем кончился предпоследний, т. е. не знаем условий, в которых мы приступаем к последнему шагу?
Вот тут-то и начинается самое главное. Планируя последний шаг, нужно сделать разные предположения о том, чем кончился предпоследний, (т–1)-й шаг, и для каждого из этих предположений найти условное оптимальное управление на m-м шаге («условное» потому, что оно выбирается исходя из условия, что предпоследний шаг кончился так-то и так-то).
Предположим, что мы это сделали и для каждого из возможных исходов предпоследнего шага знаем условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на m-м шаге. Теперь мы можем оптимизировать управление на предпоследнем, (т–1)-м шаге. Снова сделаем все возможные предположения о том, чем кончился предыдущий, (т–2)-й шаг, и для каждого из этих предположений найдем такое управление на (т–1)-м шаге, при котором выигрыш за последние два шага (из которых m-й уже оптимизирован) максимален. Так мы найдем для каждого исхода (т–2)-го шага условное оптимальное управление на (т–1)-м шаге и условный оптимальный выигрыш на двух последних шагах. Далее, «пятясь назад», оптимизируем управление на (т–2)-м шаге и т. д., пока не дойдем до первого.
Предположим, что все условные оптимальные управления и условные оптимальные выигрыши за весь «хвост» процесса (на всех шагах, начиная от данного и до конца) нам известны. Это значит: мы знаем, что надо делать, как управлять на данном шаге и что мы за это получим на “хвосте”, в каком бы состоянии ни был процесс к началу шага. Теперь мы можем построить уже не условно оптимальное, а просто оптимальное управление х* и найти не условно оптимальный, а просто оптимальный выигрыш W* .
В самом деле, пусть мы знаем, в каком состоянии S0была управляемая система (объект управления S) в начале первого шага. Тогда мы можем выбрать оптимальное управление х1*на первом шаге. Применив его, мы изменим состояние системы на некоторое новое S1*; в этом состоянии мы подошли ко второму шагу. Тогда нам тоже известно условное оптимальное управление х2*, которое к концу второго шага переводит систему в состояние S2, и т. д. Что касается оптимального выигрыша W за всю операцию, то он нам уже известен: ведь именно на основе его максимальности мы выбирали управление на первом шаге.
Таким образом, в процессе оптимизации управления методом динамического программирования многошаговый процесс «проходится» дважды: первый раз – от конца к началу, в результате чего находятся условные оптимальные управления и условные оптимальные выигрыши за оставшийся «хвост» процесса; второй раз – от начала к концу, когда нам остается только «прочитать» уже готовые рекомендации и найти безусловное оптимальное управление х*, состоящее из оптимальных шаговых управлений х1*,х2*,….хm*.
Первый этап условной оптимизации – несравненно сложнее и длительнее второго. Второй этап почти не требует дополнительных вычислений.
Общий принцип, лежащий в основе решения всех задач динамического программирования (его часто называют «принципом оптимальности»): каково бы ни было состояние системы S перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным.
Этапы решения задачи динамического программирования:
1. Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
2. Расчленить операцию на этапы (шаги).
3. Выяснить набор шаговых управлений xi для каждого шага и налагаемые на них ограничения.
4. Определить, какой выигрыш приносит на i-м шаге управление xi , если перед этим система была в состоянии S, т. е. записать «функции выигрыша»:
 (3.1)
(3.1)
5. Определить, как изменяется состояние системы Sпод влиянием управления xi на i-м шаге: оно переходит в новое состояние
 (3.2)
(3.2)
6. Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш Wi(S)(начиная с i-го шага и до конца) через уже известную функцию Wi+l(S):
 (3.3)
(3.3)
Этому выигрышу соответствует условное оптимальное управление на i-м шаге xi(S)(подчеркнем, что в уже известную функцию Wi+1(S)надо вместо Sподставить измененное состояние  .
.
7 . Произвести условную оптимизацию последнего (m-го) этапа, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле
 (3.4)
(3.4)
и находя условное оптимальное управление xm(S),для которого этот максимум достигается.
8. Произвести условную оптимизацию (т–1)-го, (т–2)-го и т.д. шагов по формуле (3.3), полагая в ней i = (т–1), (т–2), ..., и для каждого из шагов указать условное оптимальное управление xi(S), при котором максимум достигается.
Заметим, что если состояние системы в начальный момент известно (а это обычно бывает так), то на первом шаге варьировать состояние системы не нужно – прямо находим оптимальный выигрыш для данного начального состояния S0. Это и есть оптимальный выигрыш за всю операцию
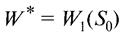
9. Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге х1* = х1*(S0); изменить состояние системы по формуле (3.2); для вновь найденного состояния найти оптимальное управление на втором шаге х2* и т. д. до конца.
Для решения задач динамического программирования мы применим сервис Excel “Поиск решения”, что позволит многократно сократить трудозатраты по сравнению с традиционной технологией.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...