
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Оптимизация сетевого графика комплекса работ
Оптимизация сетевого графикапредставляет процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.
В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути. Это достигается:
• перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;
• сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;
• параллельным выполнением работ критического пути;
• пересмотром топологии сети, изменением состава работ и структуры сети.
В процессе сокращения продолжительности работ критический путь может измениться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ новою критического пути, и так будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или по крайней мере пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится,
Весьма эффективным является использование метода статистического моделирования, основанного на многократных последовательных изменениях продолжительности работ (в заданных пределах) и "проигрывании" на компьютере различных вариантом сетевого графика с расчетами всех его временных параметров и коэффициентов напряженности работ. Процесс "проигрывания" продолжается до тех пор, пока не будет получен приемлемый вариант плана или пока не будет установлено, что все имеющиеся возможности улучшения плана исчерпаны и поставленные перед разработчиком проекта условия невыполнимы.
До сих пор мы говорили лишь о соблюдении директивных сроков выполнения комплекса работ и не затрагивали непосредственно вопросов стоимости разработки проектов. Однако па практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительно к оценкам сроков фактора стоимости работ, поэтому оптимизация сетевого графика часто проводится методом "время – стоимость".
Оптимизация сетевого графика в зависимости от полноты решаемых задач может быть условно разделена на частную и комплексную. Видами частной оптимизации сетевого графика являются: минимизация времени выполнения комплекса работ при заданной его стоимости; минимизация стоимости комплекса работ при заданном времени выполнения проекта. Комплексная оптимизация представляет собой нахождение оптимального соотношения величин стоимости и сроков выполнения проекта в зависимости от конкретных целей, ставящихся при его реализации.
При использовании метода "время – стоимость" предполагается, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. Каждая работа (i,j)характеризуется продолжительностью t(i,j), которая может находиться в пределах

где
а (i, j)–минимально возможная (экстренная) продолжительность работы (i,j);
b(i,j) — нормальная продолжительность выполнения работы (i,j).
При этом стоимость с (i, j)работы (i, j)заключена в границах от cmin(i, j)(при нормальной продолжительности работы) до cmax(i,j) ( при экстренной продолжительности работы).
Предполагается, что время выполнения работ можно сократить, вкладывая дополнительные ресурсы, причём сокращение времени пропорционально дополнительным ресурсам Х:
tнов(i ,j) = t(i , j) - h(i , j) X ( 4.5 )
Величина h(i, j), равная тангенсу угла а наклона аппроксимирующей прямой в диапазоне a(i,j), b(i,j) (см. Рис. 4.3), показывает затраты на ускорение, то есть дополнительные ресурсы, необходимые для ускорения работы на единицу времени (день).

Рис.4.3. Зависимость времени работы от дополнительных затрат.
Под ресурсами можно понимать деньги, людей, технику. На Рисунке 4.3 видно, что используемая линейная зависимость время/затраты справедлива в некотором диапазоне; существует асимптота слева (затраты, при которых работа никогда не будет сделана) и справа: минимальное время выполнения работы при любых затратах. Ограничения затрат обозначены Х– (сколько можно вычесть) и Х+ (сколько можно добавить). Эти величины могут отличаться по модулю.
Дополнительные ресурсы можно привлечь извне, а можно перераспределить внутри проекта, перебросив с малонапряжённых работ на критические.
Далее приведён пример сетевого графика, соответствующего выполнению некоего проекта. Кругами обозначены события, стрелками – работы. Расположение кружков соответствует времени наступления событий, проекции стрелок на временную ось пропорциональны временам работ, резервы времени обозначены пунктиром.
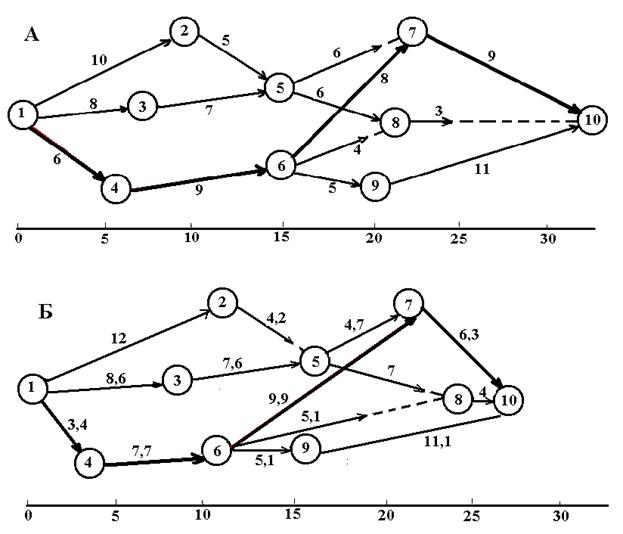 Рис.4.4. Сетевой график до (А) и после оптимизации (Б).
Рис.4.4. Сетевой график до (А) и после оптимизации (Б).
Обычно оптимизацию плана комплекса работ проводят после нахождения критических работ, напряжённостей работ и ресурсов, которые можно перебросить с некритических работ на критические. В данном случае критический путь 1=>4=>6=>7=>10, соответственно новое время выполнения комплекса работ
tкрит.нов.= t1нов+t4нов+t6нов +t7нов +t10нов. ( 4.6 )
В данной работе предлагается принципиально новая методика оптимизации сетевого графика, основанная на использовании итерационной градиентной процедуры (метод Ньютона или аналогичный), включённой в сервис “Поиск решения” (Solver) электронных таблиц Excel. Исходные данные, соответствующие сетевому графику Рис.4.4 А, и расчётные формулы размещаются в Таблице 4.2. t новое работ вычисляется по формуле (4.5), в данном примере h=0,1. Без дополнительных затрат tкрит=32. Целевая функция tкрит, её надоминимизировать, изменяя ячейки вектора Х. Ограничения:
X >= X-, X <= X+, SХ = 0,
то есть ресурсы перераспределяются внутри проекта, дополнительных затрат нет. В данном примере ограничения затрат X– = –50, X+ = 50. В реальных проектах ограничения и коэффициенты затрат на ускорение работ h устанавливаются экспертами для каждой работы отдельно, в таблице появляются ещё три столбика-вектора: h, X-, X+. Окно “Поиска решения” представлено на Рис.4.5.
Таблица 4.2.
| События | Опорные события | работа | t работ | Х | t нов. работ |
| 1-2 | |||||
| 1-3 | |||||
| 1-4 | |||||
| 2-5 | |||||
| 3-5 | |||||
| 4-6 | |||||
| 2, 3 | 5-7 | ||||
| 5-8 | |||||
| 6-7 | |||||
| 6-8 | |||||
| 6-9 | |||||
| 5, 6 | 7-10 | ||||
| 5, 6 | 8-10 | ||||
| 9-10 | |||||
| 7, 8 , 9 | |||||
| SХ | |||||
| t крит |

Рис.4.5. Окно “Поиска решения”
В результате работы “Поиска решения” получим результат:
Таблица 4.3.
| События | Опорные события | работа | t работ | Х | t нов. работ |
| 1-2 | -50 | ||||
| 1-3 | -50 | ||||
| 1-4 | |||||
| 2-5 | -50 | ||||
| 3-5 | -31,25 | 10,125 | |||
| 4-6 | |||||
| 2, 3 | 5-7 | -3,125 | 6,3125 | ||
| 5-8 | -3,125 | 6,3125 | |||
| 6-7 | |||||
| 6-8 | -3,125 | 4,3125 | |||
| 6-9 | -3,125 | 5,3125 | |||
| 5, 6 | 7-10 | ||||
| 5, 6 | 8-10 | -3,125 | 3,3125 | ||
| 9-10 | -3,125 | 11,313 | |||
| 7, 8 , 9 | |||||
| SХ | -4E-07 | ||||
| t крит |
В результате максимальных вложений в критические работы путь
1=>4=>6=>7=>10 сократился до 12, но другие пути удлинились, и время выполнения проекта по пути 1=>2=>5=>7=>10 удлинилось до 35,31. Очевидно, в ограничения "Поиска решения" надо вводить недопустимость удлинения других путей по сравнению с критическим. Но даже в нашей простой задаче это приводит большому количеству ограничений, так как надо предусмотреть все возможные пути. Поэтому мы предлагаем принципиально новую технологию расчёта, основанную на понятии опорных событий, а не опорных работ, как обычно, и вычислении времён наступления событий.Опорные события – это события, непосредственно предшествующие данному событию, и связанные с ним стрелками-работами. В таблице 4.4 представлены результаты расчётов, а на Рисунке 4.4 Б соответствующий сетевой график.t новые событийвычисляются в последних четырех столбцах таблицы. Если имеется только одно опорное событие, то время наступления события складывается из времени наступления опорного события и времени соответствующей работы. Если опорных событий несколько, то время наступления события вычисляется по всем опорным событиям в трёх последних столбцах, и максимум по этим ячейкам принимается за t новое события.Если для каких-либо событий опорных событий больше, то и количество соответствующих столбцов должно быть больше.Дополнительные ограничения: время критического пути, вычисленное по формуле ( 4.6 ), должно быть больше или равно времён наступления конечного события 10, вычисленных в последних трёх ячейках соответствующей строки. Окно “Поиска решения” представлено на Рисунке 4.6, результаты расчётов – в Таблице 4.4. Полученный результат:tкрит=27,168 ,остальные пути, приводящие к событию 10, то есть к окончанию проекта, имеют ту же длину.
Данная задача и технология её решения являются нелинейными. Это может привести к появлению различных планов Х, в том числе неоптимальных, и зависимости результатов от начальных значений Х.

Рис. 4.6. Окно “Поиска решения”
В частности, коэффициент ускорения h для всего проекта (0,0315) оказался втрое меньше h для каждой работы в отдельности (0,1). Этот результат был получен последовательным изменением SХ в параметрах “Поиска решения”. Соответствующий график представлен на Рисунке 4.7.

Рис.4.7. Изменение продолжительности проекта t в зависимости от дополнительных ресурсов SХ
Таблица 4.4.
| Собы-тия | Опорные события | Работа | t работ | Х | t нов. работ | Макс t нов. событий | t новые событий | ||
| 1-2 | -20,85 | 12,08 | |||||||
| 1-3 | -6,048 | 8,60 | |||||||
| 1-4 | 26,575 | 3,34 | |||||||
| 2-5 | 8,7497 | 4,12 | 12,08 | ||||||
| 3-5 | -6,048 | 7,60 | 8,60 | ||||||
| 4-6 | 13,448 | 7,65 | 3,34 | ||||||
| 2, 3 | 5-7 | 13,036 | 4,69 | 16,21 | 16,21 | 16,20 | |||
| 5-8 | -9,425 | 6,94 | |||||||
| 6-7 | -19,08 | 9,90 | 10,99 | ||||||
| 6-8 | -15,89 | 5,58 | |||||||
| 6-9 | -0,619 | 5,06 | |||||||
| 5, 6 | 7-10 | 27,385 | 6,26 | 20,90 | 20,90 | 20,90 | |||
| 5, 6 | 8-10 | -10,15 | 4,01 | 23,15 | 23,15 | 16,58 | |||
| 9-10 | -1,079 | 11,10 | 16,06 | ||||||
| 7, 8 , 9 | 27,168 | 27,168 | 27,168 | 27,168 | |||||
| SХ | 7E-15 | ||||||||
| t крит | 27,168 |
Таблица 4.5.
| Собы-тия | Опорные события | Работа | t работ | Х | t нов. работ | Макс t нов. событий | t новые событий | ||
| 1-2 | 10,491 | 8,9509 | |||||||
| 1-3 | 13,094 | 6,6906 | |||||||
| 1-4 | 43,911 | 1,6089 | |||||||
| 2-5 | 18,323 | 3,1677 | 8,9509 | ||||||
| 3-5 | 15,721 | 5,4279 | 6,6906 | ||||||
| 4-6 | 30,442 | 5,9558 | 1,6089 | ||||||
| 2, 3 | 5-7 | 21,185 | 3,8815 | 12,119 | 12,119 | 12,11855 | |||
| 5-8 | 10,271 | 4,9729 | |||||||
| 6-7 | -4,352 | 8,4352 | 7,5648 | ||||||
| 6-8 | -8,482 | 4,8482 | |||||||
| 6-9 | -4,078 | 5,4078 | |||||||
| 5, 6 | 7-10 | ||||||||
| 5, 6 | 8-10 | 0,9144 | 2,9086 | 17,091 | 17,091 | 12,41294 | |||
| 9-10 | 39,726 | 7,0274 | 12,973 | ||||||
| 7, 8 , 9 | |||||||||
| SХ | 237,17 | ||||||||
| t крит |
Возможна другая постановка задачи: вычислить и минимизировать количество дополнительных ресурсов SХ для достижения заданной величины tкрит.В этом случае целевой ячейкой “Поиска решения” становится SХ, и устанавливается ограничение t крит. В примере, приведённом в Таблице 4.5 , установлено tкрит=20. Расчёты показали, что это достижимо при дополнительном вложении 237,17 единиц ресурсов. Интересно, что сохраняется линейная зависимость t(SХ), что видно на Рисунке 4.8 .

Рис.4.8. Изменение продолжительности проекта t в зависимости
от дополнительных ресурсов SХ .
УПРАЖНЕНИЯ
В задачах 4.1, 4.2построить сетевой график. Найти продолжительность выполнения комплекса работ, временные характеристики событий и работ. В скобках указана продолжительность работ.
4.1. Сделать деревянный ящик (работу выполняет один человек). Разместить доски в соответствии с размерами ящика (15 мин); разрезать доски (12 мин); склеить части ящика (40 мин); прибить к крышке ящика петли (8 мин); подождать, пока ящик высохнет, и вытереть его (15 мин); петли (с крышкой) прибить к ящику (10 мин).
4.2. Заменить колесо машины (работу выполняют два человека). Достать из багажника домкрат и инструменты (40 с); снять диск с колеса (30 с); освободить колесо (50 с); поставить домкрат под машину (26 с); поднять машину (20 с); из багажника взять запасное колесо (25 с); снять гайки и колесо (20 с); установить запасное колесо на ось (10 с); завинтить (не сильно) гайки на оси (15 с); опустить машину и собрать домкрат (25 с); поставить домкрат обратно в багажник (10 с); завинтить гайки на оси до конца (12 с); положить плохое колесо и инструменты в багажник (40 с); поставить на место диск колеса (10 с).
4.3. Придумайте проекты и нарисуйте для них сетевые графики:
.а) строительство особняка; б) открытие мастерской (ювелирной и т.д);
в) полёт на Марс; г) экспедиция на полюс; г) ремонт квартиры;
д) подготовка к сессии, и т.п.

Рис. 4.9. Сетевой график
4.4. Для сетевого графика (Рис. 4.9) найти все полные пути, критический путь; рассчитать ранние и поздние сроки свершения событий, начала и окончания работ; определить резервы времени полных путей и событий, резервы времени (полные, частные резервы первого вида, свободные и независимые) работ и коэффициенты напряженности работ.
4.5. Как изменится срок выполнения проекта ( Рис. 4.9), резервы времени работ и событий, коэффициенты напряженности работ, если увеличить продолжительность работы t(9, 10) на величину: a) Rn(9, 10); б) R1(9, 10); в) Rc(9, 10); г) Rн(9, 10)?
4.6. Как изменится срок выполнения проекта ( Рис. 4.9), резервы времени работ и событий, коэффициенты напряженности работ, если продолжительность каждой работы t(i, j)увеличить на величину: : a) Rn(9, 10); б) R1(9, 10);
в) Rc(9, 10); г) Rн(9, 10)? Для случаев б), в) и г) найти все критические пути сетевого графика.
4.7.В таблице 4.6 указаны оценки времени выполнения работ сетевого графика, данные ответственными исполнителями и экспертами.
Таблица 4.6
| № п/п | Работа (i,j) | Оценки времени выполнения работы, сутки | ||
| Оптимистичес-кая t0(i,j) | Пессимистическая tn(i, j) | Наиболее вероятная tнв(i,j) | ||
| (1,2) | ||||
| (1,3) | ||||
| (1,4) | ||||
| (3,4) | ||||
| (2,5) | ||||
| (4,5) |
Необходимо: а) построить сетевой график; б) определить средние (ожидаемые) значения продолжительности работ; в) определить критический путь и его длину. Полагая, что продолжительность критического пути распределена по нормальному закону, найти: а) вероятность того, что срок выполнения комплекса работ не превысит 17 суток; б) максимальное значение продолжительности выполнения проекта, которое можно гарантировать с надежностью 0,95.
4.8.По данным таблицы 4.7 необходимо: 1) построить сетевой график; 2) определить критический путь и стоимость проекта при минимально возможных значениях продолжительности всех работ; 3) найти минимальную стоимость проекта при том же сроке его завершения; 4) рассчитать и построить оптимальную зависимость стоимости проекта от продолжительности его выполнения, используя в качестве первоначального варианта сетевого графика:
а) план с максимальными значениями продолжительности всех работ и соответственно минимальной стоимостью проекта;
б) план, полученный в результате выполнения п.З.
Таблица 4.7
| Работа | Нормальный план выполнения работы, сутки | Срочный план выполнения работы, сутки | Коэффициент затрат на ускорение работы | ||
| min | max | min | max | ||
| (1,2) | |||||
| (1,3) | |||||
| (1,4) | |||||
| (2,3) | |||||
| (2,4) | |||||
| (3,4) | |||||
| (3,5) | |||||
| (4,5) | |||||
| (5,6) |
4.9. Сократите время выполнения проектов, сетевые графики которых представлены на Рисунке 4.10 без привлечения дополнительных ресурсов (SХ=0). Для всех работ h=0,1, X- = -60, X+ = 65. Вычислите hT =DTпроекта/SХ. Сколько надо затратить ресурсов, чтобы уменьшить время выполнения каждого проекта до 50? Составьте соответствующие планы X,DT .

Рис.4.10. Сетевые графики
4.7. Сетевое планирование в условиях неопределенности
При определении временных параметров сетевого графика до сих пор предполагалось, что время выполнения каждой работы точно известно. Такое предположение в действительности выполняется редко: напомним, система СПУ обычно применяется для планирования сложных разработок, не имевших в прошлом никаких аналогов. Чаще всего продолжительность работы по сетевому графику заранее не известна и может принимать лишь одно из ряда возможных значений. Другими словами, продолжительность работы t(i,j) является случайной величиной, характеризующейся своим законом распределения, а значит, своими числовыми характеристиками –математическим ожиданием, оценкой которого является среднее значение tcp (i, j), и дисперсией s2(i, j). Практически во всех системах СПУ априори принимается, что распределение продолжительности работ обладает тремя свойствами: а) непрерывностью; б) унимодальностью, т.е. наличием единственного максимума у кривой распределения; в) двумя точками пересечения кривой распределения с осью Ох, имеющими неотрицательные абсциссы.
Кроме того, установлено, что распределение продолжительности работ обладает положительной асимметрией, т.е. максимум кривой смещен влево относительно медианы (линии, делящей площадь под кривой на две равные части). Распределение, как правило, более круто поднимается при удалении от минимального значения и полого опускается при приближении к максимальному значению t(Рис.4.11).
Простейшим распределением с подобными свойствами является известное в математической статистике b-распределение. Анализ большого количества статистических данных (хронометражи времени реализации отдельных работ, нормативные данные и т.д.) показывает, что b-распределение можно использовать в качестве априорного для всех работ.
Для определения числовых характеристик tcp(i, j), и s2(i, j) этого распределения для работы (i, j) на основании опроса ответcтвенных исполнителей проекта и экспертов определяют три временные оценки (рис. 4.11):
а) оптимистическую оценку t0(i, j), т.е. продолжительность работы (i, j) при самых благоприятных условиях;
б) пессимистическую оценку tn(i,j),т.е. продолжительность работы (i, j) при самых неблагоприятных условиях;
в) наиболее вероятную оценку tm(i,j), т.е. продолжительность работы (i, j) при нормальных условиях.

Рис.4.11. b-распределение
Предположение о b-распределении продолжительности работы (i, j) позволяет получить следующие оценки ее числовых характеристик:

Следует отметить, что обычно специалистам сложно оценить наиболее вероятное время выполнения работы tнв(i, j).Поэтому в реальных проектах используется упрощенная (и менее точная) оценка средней продолжительности работы (i, j)на основании лишь двух задаваемых временных оценок t0(i,j) и tn(i,j):
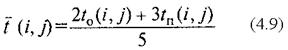
Зная t (i, j)и s2(i, j), можно определять временные параметры сетевого графика и оценивать их надежность.
Так, при достаточно большом количестве работ, принадлежащих пути L, и выполнении некоторых весьма общих условий можно применить центральную предельную теорему Ляпунова, на основании которой можно утверждать, что общая продолжительность пути Lимеет нормальный закон распределения со средним значением t (L),равным сумме средних значений продолжительности составляющих его работ t(i, j)и дисперсией s2(L),равной сумме соответствующих дисперсий s2(i, j):

Предположим, что сетевой график на рисунке 4.4 представляет сеть не с детерминированными (фиксированными), а со случайными продолжительностями работ и цифры над работами-стрелками указывают средние значения t (i, j)продолжительности соответствующих операций, найденные по формуле (4.7) или (4.9), и известны все дисперсии s2(i, j),вычисленные по формуле (4.8).
Следует отметить, что и в этом случае временные параметры сетевого графика – длина критического пути, ранние и поздние сроки свершения событий, резервы времени событий и работ и т.д. не изменятся, но при этом необходимо учесть, что эти параметры теперь будут являться средними значениями соответствующих случайных величин: средней длиной критического пути tcp.кр, средним значением раннего срока наступления события tр(i), средним значением полного резерва времени работы Rn(i,j)и т.п.
Так, tcp.кр=32будет означать, что длина критического пути лишь в среднем составляет 32 суток, а в каждом конкретном проекте возможны заметные отклонения длины критического пути от ее среднего значения (причем, чем больше суммарная дисперсия продолжительности работ критического пути, тем более вероятны значительные по абсолютной величине отклонения).
Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров сети. Весьма важным моментом анализа становится оценка вероятности того, что срок выполнения проекта tKpне превзойдет заданного директивного срока Т.
Полагая tкр случайной величиной, имеющей нормальный закон распределения, получим


Рис.4.12. Интеграл вероятностей Лапласа.
(на рис. 4.12 это площадь заштрихованной фигуры), где Ф(z) — значение интеграла вероятностей Лапласа, где z = (Т -tcpкр)/ sткр ;
sкр — среднее квадратическое отклонение длины критического пути:
a tcp кр, s2кр определяются по формулам (4.7) и (4.8).
Если вероятность Р(tкр < Т)мала (например, меньше 0,3), то опасность срыва заданного срока выполнения комплекса велика, необходимо принятие дополнительных мер (перераспределение ресурсов по сети, пересмотр состава работ и событий и т.п. — об этом речь пойдет дальше). Если Р(tкр< Т)значительна (например, более 0,8), то, очевидно, с достаточной степенью надежности можно прогнозировать выполнение проекта в установленный срок.
В некоторых случаях представляет интерес и решение обратной задачи: определение максимального срока выполнения проекта Т, который возможен с заданной надежностью (вероятностью) р. В этом случае
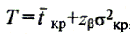
где zb — нормированное отклонение случайной величины, определяемое с помощью функции Лапласа Ф(zb)= b
. Задача. Пусть, например, для сети (рис. 4.10) дисперсии продолжительности работ критического пути равны: s2(0,3)=2,5', s2(3,5) = 2,1; s2(5,5)=3,2; s2(6,9)=4,0; s2(9,10)=1,5; s2(10,11)=3,5.Оценить вероятность выполнения проекта в срок Т = 63 суткам.
Решение: s2кр = s2(0,3) + s2(3,5) + s2(5,6) + s2(6,9) + s2(9,]0) + s2(10,11)=
= 2,5 + 2,1 + 3,2 + 4,0 + 1,5 + 3,5 = 16,8; s= 4,1.
Теперь искомая вероятность



=0,5 + 0,5*0,376 = 0,688
то есть можно с известным риском предполагать выполнение проекта в срок.
Рассмотрим и пример решения обратной задачи: оценить максимально возможный срок Твыполнения проекта с надежностью b=0,95.
T=61+z(0,95)*4,1=61+l,96*4,1=69, т.е. с надежностью 0,95 срок выполнения проекта не превысит 69 суток.
Следует отметить, что для данной сети мы можем найти лишь весьма приближенные оценки Р(tкр< Т)и Т, ибо на основании теоремы Ляпунова вывод о нормальном законе распределения случайной величины tкр правомерен лишь для достаточно большого числа критических работ, а в рассматриваемой сети их всего 6.
Однако приведенный метод расчета имеет принципиальные недостатки оценки параметров даже сложных сетей с большим количеством работ. Дело в том, что на практике нередки случаи, когда дисперсии s2(L) длин некритических (но близких к критическому) путей существенно больше, чем s2кр. Поэтому при изменении ряда условий в данном конкретном комплексе работ возможен переход к новым критическим путям, которые в расчете не учитываются.
Различия между событиями с детерминированными случайными продолжительностями работ не следует путать с различием детерминированных и стохастических сетей. Последнее различие связано со структурой самой сети.
Рассмотренные до сих пор сети являлись детерминированными, хотя работы в них могли характеризоваться не только детерминированными, но и случайными продолжительностями. Вместе с тем встречаются проекты, когда на некоторых этапах тот или иной комплекс последующих работ зависит от неизвестного заранее результата. Какой из этих комплексов работ будет фактически выполняться, заранее не известно, а может быть предсказано лишь с некоторой вероятностью. Например, может быть предусмотрено несколько вариантов продолжения исследования в зависимости от полученных опытных данных или несколько вариантов строительства предприятий различной мощности по обработке сырья в зависимости от результатов разведки запасов этого сырья. Такие сети называются стохастическими.
В свою очередь стохастические сети, так же как и детерминированные, могут характеризоваться детерминированными либо случайными продолжительностями.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...