
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Выбор оптимального пути в транспортной сети
(задача коммивояжёра)
Постановка задачи: выбрать оптимальный маршрут поездки из одного города в другой с заездом в указанные города. Решим задачу, используя Сервис “Поиск решения” (Solver) Excel, основанный на итерационной процедуре последовательного приближения к экстремуму целевой функции при соблюдении ограничений (метод Ньютона, сопряжённых градиентов или другие).
Транспортная сеть состоит из n узлов (будем называть их также пунктами или городами), некоторые из которых соединены магистралями. Стоимость проезда по каждой из таких магистралей известна и отмечена на схеме (Рисунок 5.1). Надо найти оптимальный маршрут проезда из 0-го пункта в n-ый с заездом в указанные пункты. В данном примере целевая функция – суммарная стоимость проезда, а область допустимых решений является дискретным множеством – набором единиц и нулей, означающих проезд из одного города в другой или отказ от проезда.
Пусть сеть состоит из 11 узлов, соединённых магистралями согласно схеме. Стоимость проезда (или расстояние) из пункта i в пункт k равна Rik, и элементы этой матрицы приведены на схеме.

Рис.5.1. Транспортная сеть.
Найдём оптимальный маршрут из 0-го пункта в 11-ый.
Для решения задачи надо построить таблицы: Стоимость проезда (расстояния) Rik ; План поездки Xik, который в данном случае представляет из себя матрицу из единиц и нулей, соответствующих перемещению или не перемещению из одного пункта в другой; таблицу произведений Rik Xik, то есть расходов на поездки (Затраты). Таблицы симметричны относительно диагонали, то есть возможны поездки в любом направлении; это даёт возможность произвольной нумерации пунктов, кроме первого и последнего. Решение задачи сводится к поиску комбинации Xik , обеспечивающей проезд из пункта 0 в пункт 11 при минимальных затратах. Целевая функция в данной задаче – сумма по таблице Затраты SS XikRik . Её надо минимизировать, изменяя ячейки таблицы План поездки Xik, при ограничениях: все Xik двоичные (0 или 1); если есть приезд в город, должен быть выезд; выезд из пункта 0 и прибытие в последний обязательны. Для программирования этих условий надо суммировать строки и столбцы таблицы План поездкиXik; ненулевое значение суммы по строке означает выезд из соответствующего пункта (из п.0 обязательно); ненулевое значение в сумме по столбцу означает приезд в соответствующий пункт (в п.11 обязательно). Приезд в какой-либо пункт, кроме п.11, требует обязательного выезда из него, т.е. соответствия сумм по столбцам суммам по строкам.
Количество ячеек в таблице Xik достаточно велико, и компьютер может не справиться с решением задачи. Поэтому предлагается принципиально новый подход: создание дополнительной таблицы План поездкив компактном виде, из которой копируются значения в зависимые от нее ячейки таблицы План поездкиXik. В ячейки таблицы План поездки Xik вносятся формулы, связывающие ее с таблицей План поездки в компактном виде, в которую вносится единицы, нули или опорный план на основе мнений экспертов.
Найдём оптимальный маршрут из п.0 в п.11 без дополнительных ограничений. В таблицах 5.2, 5.3 и 5.4 представлены результаты работы “Поиска решения”.
Таблица 1. Стоимость проезда (расстояния) Rik
куда
| откуда | ||||||||||||
Таблица 5.2. План поездкиXik.
| B | C | D | E | F | G | H | I | J | K | L | M | N | ||
| откуда | выезд | |||||||||||||
 1 1
| ||||||||||||||

|  1 1
| |||||||||||||
| приезд |
Таблица 5.3. План поездки в компактном виде.
| C | D | E | F | G | H | I | J | K | L | M | N | |
Таблица 5.4. Затраты Rik Xik . Нули и пустые строки удалены.
| Куда | ||||||||||||
| откуда | ||||||||||||
| Целе-вая | ||||||||||||
| S |
В окне “Поиска решения” следует задать: Целевую ячейку SS XikRik, Изменяя ячейки – План поездки в компактном виде, Ограничения: План поездки в компактном виде двоичные; суммы по строкам таблицы План поездки Xik (приезд), начиная со второй (с п.1) должны равняться суммам по столбцам (приезд), исключая последнее значение, п.11 (N31:N40= C42:L42). Суммы по первой строке (выезд из п.0, N30) и последнему столбцу (приезд в п.11, M42) не должны равняться 0. Запустите Выполнить.

Рис.5.2. Окно “Поиска решения”
Оптимальный план поездки: пункты 0 => 2 => 6 => 11, стоимость 48 у.е. (Эту технологию можно использовать для нахождения критического пути в сетевом графике комплекса работ, только целевую функцию надо максимизировать. Критический путь 0=>3=>8=>10=>11, длина 112).
Приезд в город становится обязательным, если введено дополнительное ограничение – неравенство нулю суммы по соответствующему столбцу таблицы План поездки. Возможны несколько заездов, то есть сумма может быть больше 1. Если необходимо сделать обязательным приезд в один из группы городов – вычислите сумму по ячейкам приезда в эти города и введите ограничение: эта сумма больше или равна единице.
Наиболее интересная задача – спланировать маршрут, проходящий через все узлы сети. В общем виде эта “Задача коммивояжёра” до сих пор не решена. Попробуем решить её с помощью компьютера. Для этого надо ввести дополнительное ограничение: все суммы по столбцам таблицы План поездки должны быть больше или равны 1. Полученный результат:
0=>1=>2=>6=>7=>9=>10=>11 и отдельно 3=>8=>3 и 4=>5=>4, стоимость 165 у.е. Компьютер выполнил все условия, но два “острова” 4-5 и 3-8 оказались не связанными с основным маршрутом. Решить задачу в общем виде не удаётся, но для практических целей эту технологию можно использовать. Для этого надо ввести дополнительные ограничения, вынуждающие компьютер войти на “острова” с основного маршрута.
В данном примере на остров 3-8 можно попасть по маршрутам 0-3, 9-3 и 10-8, на остров 4-5 по маршрутам 1-4, 6-5 и 11-5. Исходя из конкретной ситуации, поставив ограничения: больше или равно единице в ячейках 9-3 (Е38³1) и 1-4 (F30³1) получим маршрут 0=>1=>2=>1=>4=>5=>6=>7=> 9=>3=>8=>10=>11, стоимость 192 у.е. При этом пункт 1 посещается дважды. Этот маршрут не вполне оптимален. Если указать на маршрут 0=>2 (D29=1), то получится 0=>2=>1=>4=>5=>6=>7=>9=> 3=>8=>10=>11, стоимость которого 190 у.е.
Таблица 5.5. План поездкиXik.
| B | C | D | E | F | G | H | I | J | K | L | M | N | ||
| откуда | выезд | |||||||||||||

|  1 1
| |||||||||||||

| ||||||||||||||
| -0 | ||||||||||||||

| 
| |||||||||||||

|  
| |||||||||||||
 1 1
| ||||||||||||||

| ||||||||||||||
 1 1
| ||||||||||||||
| приезд |
Можно предоставить компьютеру большую свободу выбора маршрута на острова. Для этого надо суммировать содержимое ячеек таблицы План поездкиXik , соответствующим входам на острова, и в “Поиске решения” потребовать для этих сумм ограничения ³1. Но, как показали эксперименты, при этом могут появиться новые острова.
При решении данной задачи проявилось свойство задач нелинейного программирования: компьютер может найти различные маршруты, соответствующие локальным минимумам целевой функции в зависимости от опорного плана.
Наиболее сложный вариант данной задачи – объехать все пункты сети с возвращением в исходный пункт. Маршрут приходится разбивать на две части: “вперёд” и обратно, иначе компьютер разбивает сеть на множество “островов”. В данном случае, исходя из топологии сети, её можно разбить следующим образом: пункты 0, 1, 4, 5, 6, 7, 11, причём п.7 – конечный, так как он ближе к другому кластеру 3, 8, 9, 10, 0, и в нём п.7 является начальным. При дополнительных ограничениях на ячейки План поездки: запрет маршрута 0=>7 (иначе образуется остров) и Сумма ячеек 1-4 и 6-5 больше или равна 1, получается маршрут 0=>2=>1=>4=>5=>6=>11=>6=>7, стоимость 105 у.е. Обратный путь проще, компьютер решает задачу без дополнительных ограничений и выдаёт маршрут 7=>9=>10=>8=>3=>0, стоимость 118 у.е. Таким образом, общая стоимость поездки 223 у.е.
ВЫВОДЫ: Итерационные градиентные методы, встроенные в сервис “Поиск решения” Excel, можно использовать для выбора кратчайшего маршрута через сеть, в том числе с заездом в заданные пункты или во все. В общем виде задача с заездом во все пункты не решается, но решается путём взаимодействия человека и компьютера: человек задаёт разумный опорный план и ограничения, помогающие компьютеру решить задачу.
Модели управления запасами
6.1. Основные понятия
Задачи управления запасами составляют один из наиболее многочисленных классов экономических задач исследования операций, решение которых имеет важное народнохозяйственное значение. Правильное и своевременное определение оптимальной стратегии управления запасами, а также нормативного уровня запасов позволяет высвободить значительные оборотные средства, замороженные в виде запасов, что в конечном счете повышает эффективность используемых ресурсов.
Что можно понимать под запасами (резервами) в финансовой деятельности? Это запас наличных денег в банке, чтобы можно было в любой момент удовлетворить все возникающие требования. Эти деньги не приносят дохода, и упущенный доход можно считать платой за их хранение. Запас денег повышает вероятность ограбления и ущерб от него, что аналогично расходам на хранение, плата за инкассацию аналогична плате за пополнение запаса. В сфере информационных технологий омертвлёнными ресурсами можно считать расходы на безопасность и скорость работы систем, и их оптимизация является важной практической задачей. Мы будем рассматривать классические модели управления запасами, так как они нагляднее, но будем помнить об их приложении к сфере финансов и IT.
Рассмотрим основные характеристики моделей управления запасами.
Спрос. Спрос на запасаемый продукт может быть детерминированным (в простейшем случае — постоянным во времени) или случайным. Случайность спроса описывается либо случайным моментом спроса, либо случайным объемом спроса в детерминированные или случайные моменты времени.
Пополнение склада. Пополнение склада может осуществляться либо периодически через определенные интервалы времени, либо по мере исчерпания запасов, т. е. снижения их до некоторого уровня.
Объем заказа. При периодическом пополнении и случайном исчерпании запасов объем заказа может зависеть от того состояния, которое наблюдается в момент подачи заказа. Заказ обычно подается на одну и ту же величину при достижении запасом заданного уровня — так называемой точки заказа.
Время доставки. В идеализированных моделях управления запасами предполагается, что заказанное пополнение доставляется на склад мгновенно. В других моделях рассматривается задержка поставок на фиксированный или случайный интервал времени.
Стоимость поставки. Как правило, предполагается, что стоимость каждой поставки слагается из двух компонент — разовых затрат, не зависящих от объема заказываемой партии, и затрат, зависящих (чаще всего — линейно) от объема партии.
Издержки хранения. В большинстве моделей управления запасами считают объем склада практически неограниченным, а в качестве контролирующей величины служит объем хранимых запасов. При этом полагают, что за хранение каждой единицы запаса в единицу времени взимается определенная плата.
Штраф за дефицит. Любой склад создается для того, чтобы предотвратить дефицит определенного типа изделий в обслуживаемой системе. Отсутствие запаса в нужный момент приводит к убыткам, связанным с простоем оборудования, неритмичностью производства и т. п. Эти убытки в дальнейшем будем называть штрафом за дефицит.
Номенклатура запаса. В простейших случаях предполагается, что на складе хранится запас однотипных изделий или однородного продукта. В более сложных случаях рассматривается многономенклатурный запас (см. раздел 8).
Структура складской системы. Наиболее полно разработаны математические модели одиночного склада. Однако на практике встречаются и более сложные структуры: иерархические системы складов с различными периодами пополнения и временем доставки заказов, с возможностью обмена запасами между складами одного уровня иерархии и т. п. (В финансовой сфере – это взаимное кредитование и кредитование в Центральном банке. В Интернете – маршрутизаторы, распределяющие трафик по менее загруженным линиям связи).
В качестве критерия эффективности (целевой функции) принятой стратегии управления запасами выступает функция затрат (издержек),представляющая суммарные затраты на хранение и поставку запасаемого продукта (в том числе потери от порчи продукта при хранении и его морального старения, потери прибыли от омертвления капитала и т. п.) и затраты на штрафы.
Управление запасами состоит в отыскании такой стратегии пополнения и расхода запасами, при котором функция затрат принимает минимальное значение.
Ниже рассматриваются простейшие модели управления запасами.
Пусть функции A(t), B(t) и R(t)выражают соответственно пополнение запасов, их расход и спрос на запасаемый продукт за промежуток времени
[0, t]. В моделях управления запасами обычно используются производные этих функций по времени a(t), b(t), r(t),называемые соответственно интенсивностями пополнения, расхода и спроса.
Если функции a(t), b(t), r(t)–не случайные величины, то модель управления запасами считается детерминированной, если хотя бы одна из них носит случайный характер – стохастической. Если все параметры модели не меняются во времени, она называется статической,в противном случае – динамической. Статические модели используются, когда принимается разовое решение об уровне запасов на определенный период, а динамические – в случае принятия последовательных решений об уровнях запаса или корректировке ранее принятых решении с учетом происходящих изменений.
Уровень запаса в момент t определяется основным уравнением запасов
J(t) = J0 + A(t) – B(t) (6.1)
где J0 – начальный запас в момент t = 0.
Уравнение (16.1) чаще используется в интегральной форме:
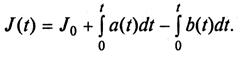
Пример 6.1.Интенсивность поступления деталей на склад готовой продукции цеха составляет в начале смены 5 дет./мин, в течение первого часа линейно возрастает, достигая к концу его 10 дет./мин, и затем остается постоянной. Полагая, что поступление деталей на склад происходит непрерывно в течение всех семи часов смены, а вывоз деталей со склада производится только в конце работы, записать выражение для уровня запаса в произвольный момент времени и, используя его, найти количество деталей на складе: а) через 30 мин после начала работы; б) в конце смены.
Решение. По условию в течение смены не происходит выдачи деталей со склада, т. е. b(t) = 0. Интенсивность пополнения запаса в течение первого часа линейно возрастает, т. е. a(t) = kt + b. Учитывая, что а(0) =5, получаем b = 5. Так как в конце часа, т. е. при t = 60 a(60) = 10, то 10 = k • 60 + 5, откуда k = 1/12. Таким образом, для первого часа смены a(t) = (1/12)t + 5 , а затем a(t) =10.
Учитывая продолжительность смены (7 ч = 420 мин) и соотношение (16.2), получаем:

Количество деталей на складе через 30 мин после начала работы:
J(30) = 900/24 + 5x30 = 187,5
а в конце смены:
J(420) = 10x420 - 150 = 4050.
6.2. Статическая детерминированная модель без дефицита
Предположение о том, что дефицит не допускается, означает полное удовлетворение спроса на запасаемый продукт, т.е. совпадение функций r(t) и b(t). Пусть общее потребление запасаемого продукта за рассматриваемый интервал времени Q равно N. Рассмотрим простейшую модель, в которой предполагается, что расходование запаса происходит непрерывно с постоянной интенсивностью, т.е. b(t) = b. Эту интенсивность можно найти, разделив общее потребление продукта на время, в течение которого он расходуется:
b=N/Q (6.3)
Пополнение заказа происходит партиями одинакового объема, т.е. функция a(i)не является непрерывной: a(t) = 0 при всех t, кроме моментов поставки продукта, когда a(t) = n, где n — объем партии. Так как интенсивность расхода равна b, то вся партия будет использована за время
Т = n/b (6.4)

Рис. 6.1 Расход и пополнение запаса Рис.6.2 Издержки
Если отсчет времени начать с момента поступления первой партии, то уровень запаса в начальный момент равен объему этой партии n, т.е.
J(0) = п. Графически уровень запаса в зависимости от времени представлен на рисунке 6.1.
На временном интервале [0, T] уровень запаса уменьшается по прямой
J(t) =п - btот значения n до нуля. Так как дефицит не допускается, то в момент T уровень запаса мгновенно пополняется до прежнего значения пза счет поступления партии заказа. И так процесс изменения J(t) повторяется на каждом временном интервале продолжительностью Т (см. рис. 6.1).
Задача управления запасами состоит в определении такого объема партии п, при котором суммарные затраты на создание и хранение запаса были бы минимальными.
Обозначим суммарные затраты через С, затраты на создание запаса – через С1,затраты на хранение запаса – через С2и найдем эти величины за весь промежуток времени Т.
Пусть затраты на доставку одной партии продукта, не зависимые от объема партии, равны с1,а затраты на хранение одной единицы продукта в единицу времени – с2. Так как за время 0 необходимо запастись Nединицами продукта, который доставляется партиями объема n, то число таких партий k равно:

Отсюда получаем

Мгновенные затраты хранения запаса в момент времени tравны с2(J(t). Значит, за промежуток времени [0, Т]они составят

или, учитывая (6.4)

Средний запас за промежуток [0, Т]равен пТ/2, т.е. затраты на хранение всего запаса при линейном (по времени) его расходе равны затратам на хранение среднего запаса.
Учитывая периодичность функции J(t) (всего за промежуток
времени Q будет k = N/n"зубцов", аналогичных рассмотренному
на отрезке [0, Т] ), и формулу (6.5), получаем, что затраты хранения запаса за промежуток времени Q равны:
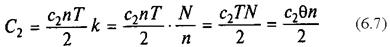
Нетрудно заметить, что затраты С1обратно пропорциональны, а затраты C2прямо пропорциональны объему партии п. Графики функций С1 (n) и C2 (n), а также функции суммарных затрат

приведены на рисунке 6.2. В точке минимума функции С(n) ее производная
 (6.9)
(6.9)
Откуда

или, учитывая (6.3):
 (6.10)
(6.10)
Формула (6.10), называемая формулой Уилсона илиформулой наиболее экономичного объема партии,широко используется в экономике. Эта формула может быть получена и другим способом, если учесть, что произведение

есть величина постоянная, не зависящая от п. В этом случае, как известно, сумма двух величин принимает наименьшее значение, когда они равны, т. е.
С1 = С2 или
 (6.11)
(6.11)
откуда получаем (6.9).
Из (6.11) следует, что минимум общих затрат задачи управления запасами достигается тогда, когда затраты на создание запаса равны затратам на хранение запаса. При этом минимальные суммарные затраты
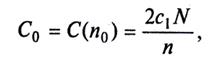 (6.12)
(6.12)
откуда, учитывая (6.9) и (6.3), получим

или
 (6.13)
(6.13)
Число оптимальных партий за время Q с учетом (6.5), (6.9) и (6.3) равно:
Время расхода оптимальной партии на основании (6.4) с учетом (6.9) и (6.3) равно

или

Задача 6.2. Потребность сборочного предприятия в деталях некоторого типа составляет 120 000 деталей в год, причем эти детали расходуются в процессе производства равномерно и непрерывно. Детали заказываются раз в год и поставляются партиями одинакового объема, указанного в заказе. Хранение детали на складе стоит 0,35 ден. ед. в сутки, а поставка партии – 10 000 ден. ед. Задержка производства из-за отсутствия деталей недопустима. Определить наиболее экономичный объем партии и интервал между поставками, которые нужно указать в заказе (предполагается, что поставщик не допускает задержки поставок).
Решение. По условию затраты на одну партию составляют C1 = 10 000 ден. ед., затраты хранения единицы запаса в сутки с1 = 0,35 ден. ед. Общий промежуток времени Q = 1 год = 365 дней, а общий объем запаса за этот период N = 120 000 деталей. По формуле (6.9)

а по (6.14)

Итак, наиболее экономичный объем партии равен 4335 деталей, а интервал между поставками ~ 13 дней.
На практике, естественно, объем партии может отличаться от оптимального n, вычисленного по (6.9). Так, в предыдущей задаче может оказаться удобным заказывать партии по 4 500 или даже по 5 000 деталей и возникает вопрос, как при этом изменятся суммарные затраты.
Для ответа на этот вопрос разложим функцию С(n) в ряд Тейлора в окрестности точки n0, ограничившись первыми тремя членами ряда при достаточно малых изменениях объема партии Dn:

или

Формула (6.16) свидетельствует об определенной устойчивости суммарных затрат по отношению к наиболее экономичному объему партии, ибо при малых Dn относительное изменение затрат примерно на порядок меньше относительного изменения объема партии по сравнению с оптимальным.
Задача 6.3. По условию задачи 6.2определить, на сколько процентов увеличатся затраты на создание и хранение запаса по сравнению с минимальными затратами при объеме заказываемых партий 5 000 деталей.
Решение. Относительное изменение объема партии по сравнению с оптимальным n0 = 4335 составляет Dn /n0 = (5000 - 4335)/4335=0,153. В соответствии с (6.16) относительное изменение суммарных затрат составит  или лишь 1,2%.
или лишь 1,2%.
Задача 6.4. В условиях задачи 6.3 предположим, что заказываются не все партии сразу, а каждая отдельно, причем срок выполнения заказа равен 16 дней. Определить точки заказа, т. е. при каком уровне запаса следует заказывать следующую партию.
Решение. Так как по результатам решения задачи 6.2длина интервала между поставками равна 13,2 дней, то заказ в условиях налаженного производства следует возобновить, когда уровень запаса достаточен для удовлетворения потребности на 16 – 13,2 = 2,8 дня. Так как ежедневная потребность (интенсивность расхода запаса) равна по формуле (6.3) b–120 000/365 = 329 деталей, то заказы должны делаться регулярно при достижении уровня запаса 329 • 2,8 = 922 деталей.
6.3. Статическая детерминированная модель с дефицитом
В рассматриваемой модели будем полагать наличие дефицита. Это означает, что при отсутствии запасаемого продукта, т.е. при J(t) = 0 спрос сохраняется с той же интенсивностью r(i) = b, но потребление запаса отсутствует: b(t) = 0, вследствие чего накапливается дефицит со скоростью b. График изменения уровня запаса в этом случае представлен на рисунке 6.3. Убывание графика ниже оси абсцисс в область отрицательных значений в отличие от графика на рисунке 6.2 характеризует накопление дефицита.
На рисунке 6.3 видно, что каждый период "пилы" Т =n/bразбивается на два временных интервала, т. е. Т = Т1 + T2, где Т1 –время, в течение которого производится потребление запаса, Т2–время, когда запас отсутствует и накапливается дефицит, который будет перекрыт в момент поступления следующей партии.

Рис. 16.3 Модель с дефицитом
Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса sв момент поступления каждой партии теперь не равен ее объему я, а меньше его на величину дефицита п–s, накопившегося за время Т2(рис. 6.3).
Из геометрических соображений легко установить, что

В данной модели в функцию суммарных затрат С наряду с затратами С1(на пополнение запаса) и С2 (на хранение запаса) необходимо ввести затраты С3 на штраф из-за дефицита, т.е. С = С1+ С2+С3.
Затраты С1 как и ранее, находим по формуле (6.11). В разделе 6.2 было показано, что затраты С2 при линейном расходе запаса равны затратам на хранение среднего запаса, который за время потребления = Т1 равен s= Т1 /2; поэтому с учетом (6.7) и (6.5) эти затраты составят

При расчете затрат С3 будем считать, что штраф за дефицит составляет в единицу времени с3 на каждую единицу продукта. Так как средний уровень дефицита за период Т2равен (п - s) Т2/2, то штраф за этот период Т2составит -0,5с3(n - s)T2, а за весь период Q с учетом (16.7)

Теперь, учитывая (6.12), (6.18) и (6.19), суммарные затраты равны

Нетрудно заметить, что при п = sформула (6.19) совпадает с ранее полученной (6.8) в модели без дефицита.
Рассматриваемая задача управления запасами сводится к отысканию такого объема партии п и максимального уровня запаса s, при которых функция С (6.19) принимает минимальное значение. Другими словами, необходимо исследовать функцию двух переменных С(п, s)на экстремум. Приравнивая частные производные дС/дп, дC/дsк нулю, получим после преобразований систему уравнений:

Решая систему, получаем формулы наиболее экономичного объема партии n0 и максимального уровня запаса s0 для модели с дефицитом:
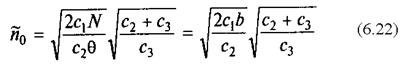

Величина

называется плотностью убытков из-за неудовлетворенного спроса и играет важную роль в управлении запасами. Заметим, что 0 £r £ 1. Если значение с3 мало по ср
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...