
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Марковские векторные процессы и последовательности
Марковские процессы являются частным видом случайных процессов. Они широко и успешно применяются при решении прикладных задач в современной технике. Практическое значение имеют различные типы случайных марковских процессов, изучаемых в теории.
Впервые такие процессы изучались русским математиком Марковым А.А. (1856 - 1922).
В соответствие с классификацией случайных процессов, рассмотренной в теме 2, марковские процессы имеют классификацию:
| Тип | Аргумент | Процесс | Название процесса |
| H | H | Непрерывный процесс | |
| D | H | Непрерывнозначная последовательность | |
| H | D | Дискретный процесс | |
| D | D | Дискретная последовательность | |
| H | H+D | Смешанный процесс |
Векторный процесс называется марковским (точнее, марковским первого порядка), если закон распределения его значений Y(tk+1) в любой будущий момент времени зависит только от значений в данный момент времени Y(tк) (непосредственно предшествующий будущему) и не зависит от того, какие значения принимал этот процесс в моменты времени, предшествующие данному Y(tк-1) (т.е. по какой траектории этот процесс пришел в данную точку).
Сформулированное положение выражается формулой
 , (1)
, (1)
т.е. условная плотность распределения вероятностей (ПРВ) в любой момент времени tk зависит только от непосредственно предшествующих значений и не зависит от всех предыдущих значений.
Для марковских процессов многомерная ПРВ
 (2)
(2)
Следовательно, для марковского случайного процесса плотности вероятности полностью определяется двумя функциями:
 – первая функция плотности вероятности
– первая функция плотности вероятности
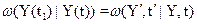 – плотность вероятности перехода
– плотность вероятности перехода
Для этих функций должны выполняться условия нормировки.
 . (3)
. (3)
При совпадении моментов времени t΄ = t
 . (4)
. (4)
Плотность вероятности перехода удовлетворяет интегральному уравнению Смолуховского-Колмогорова-Чепмена при t1<t΄<t2
 . (5)
. (5)
Аналогом формулы полной вероятности (Р(В)=Р(А)P(B|A)) является формула
 . (6)
. (6)
Если эволюция вектора состояния системы управления представлена марковским процессом, то векторно-матричное уравнение модели системы имеет вид.
 , (7)
, (7)
где D(t) – матрица коэффициентов, φ(Y,t) – векторная функция произвольного типа, H(Y,t) – матрица нелинейных функций, ξ – гауссовый белый шум. (7) – стохастическое уравнение векторного марковского процесса.
Каждая компонента yk векторного процесса Y = [y1…y2…yn], являющаяся фазовой координатой, представляет собой компоненту многомерного марковского процесса.
Однако отдельно взятая компонента yk не является одномерным марковским процессом первого порядка. (Теорема доказана Дж. Дубом).
Для дискретных систем эволюция вектора состояния описывается рекурсивной формулой
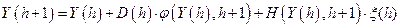 . (8)
. (8)
Выражение (8) является марковской дискретной последовательностью (марковской цепью).
Основной задачей вероятностного анализа марковских процессов является определение плотностей вероятности ω(Y,t) или плотностей вероятности перехода ω(Y΄,t΄)(Y,t).
Примером марковского процесса является так называемый винеровский случайный одномерный процесс, называемый также диффузионным, т.к. он связан с физическим явлением диффузии.
Физическим примером такого процесса является случайное блуждание броуновской тяжелой частицы под воздействием ударов молекул.
 , (9)
, (9)
 , (10)
, (10)
m – масса частицы; L – путь проходимый частицей.
ξ(t) – случайная функция, характеризующая силу толчков молекул вдоль горизонтальной оси и представляющая собой диффузионный (винеровский процесс. ξ(t) в данном случае является нормальным (гауссовым белым шумом)
Случайный процесс V(t) в данном случае представляет собой диффузионный (вигнеровский) процесс.
Следовательно, одномерная (первая) плотность вероятности процесса V(t) также гауссова. Плотность вероятности его имеет вид

Уравнение Фоккера – Планка - Колмогорова
Эволюция функций ω1(Y,t) и ω(Y΄,t΄|Y,t) описывается дифференциальным уравнением в частных производных параболического типа, которое называется уравнением Фоккера – Планка – Колмогорова (ФПК). Это уравнение получается на основе выражений (6), (7) следующим образом:
1) На основе обратного преобразования Фурье из уравнения Смолуховского – Колмогорова – Чепмена получается уравнение для характеристической функции (см. тему 1) марковского процесса.
2) Характеристическая функция раскладывается в ряд Тейлора по условным начальным моментам.
3) Производится переход к плотности вероятности на основе преобразования Фурье.
4) Перейдя к пределу при ∆t→0 и использовав уравнение (6) получается уравнение ФПК.
Для одномерного марковского процесса уравнение Фоккера – Планка – Колмогорова имеет вид:
 . (11)
. (11)
A(y,t) и B(y,t), называемые локальными характеристиками случайного процесса, определяются следующим образом:
 , (12)
, (12)
 . (13)
. (13)
y* - конкретное фиксированное значение y.
По традиции, связанной с применением уравнения ПФК в физике, коэффициенты A(y,t) и B(y,t) называются соответственно коэффициентами сноса (переноса) и диффузии.
Уравнение (11) часто записывают в другом виде, вводя так называемую функцию π(y,t) – плотность потока вероятности.
 (14)
(14)
тогда  (15)
(15)
Для функции плотности вероятности перехода ω(y΄,t΄|y,t) вид уравнения ФПК аналогичен.
Для векторного (многомерного) марковского процесса уравнение ФПК имеет вид:
 (16)
(16)
 (17)
(17)
 - оператор градиента по компонентам вектора Y.
- оператор градиента по компонентам вектора Y.

 . (18)
. (18)
 - дивергенция вектора π(Y,t). В данном случае A(Y,t) – вектора сноса, B(Y,t) – матрица диффузии марковского процесса.
- дивергенция вектора π(Y,t). В данном случае A(Y,t) – вектора сноса, B(Y,t) – матрица диффузии марковского процесса.
В качестве примера рассмотрим систему первого порядка описываемую уравнением
 (19)
(19)
a и c – коэффициенты, ξ – белый шум интенсивности G.
Уравнение ФПК для данного процесса имеет вид (11) или (15). Коэффициенты сноса и диффузии равны следующим значениям: 
Характер изменения плотности вероятности для различных моментов имеет вид

Для представленных на рисунке плотностей вероятности 0<t1<t2<t3.
При t0=0 плотность вероятности равна δ – функции в точке y = y0.
За счет коэффициента сноса A=a∙y максимум плотности вероятности смещается на величину At, а отличный от нуля коэффициент диффузии B =с2∙G обуславливает уменьшение этого максимума тем интенсивнее, чем больше коэффициент B.
Методы решения уравнения Фоккера-Планка-Колмогорова
Уравнение ФПК принадлежит к дифференциальным уравнениям в частных производных параболического типа.
Для интегрирования таких уравнений разработаны различные аналитические, в том числе приближенные методы.
1. Метод разделения переменных применим, если вектор сноса A(y,t) = A(y) и матрица диффузии B(y,t) = B(y) не зависят от времени.
Решение уравнения ПФК описывается в виде произведения двух функций, одна из которых зависит от вектора Y, а другая – только от времени.
Для многомерных систем применение метода существенно затруднено.
2. Метод замены независимых переменных сводиться к тому, чтобы путем перехода к новым координатам упростить уравнение ФПК. Общего подхода здесь нет. Для конкретных задач разработаны приемы пригодные для одномерного процесса.
3. Метод преобразования Лапласа применим к одномерным уравнениям. Смысл его состоит в том, чтобы устранить переменную t. При этом уравнение в частных производных сводится к обыкновенному дифференциальному уравнению относительно изображения функции ω(y,t).
4. Метод характеристических функций состоит в решение уравнения для характеристической функции с последующим применением преобразования Фурье для получения плотности вероятности.
Метод применим к многомерным уравнениям. Аналитическое решение может быть получено в тех задачах, в которых вектор сноса A(Y,t) является линейной функцией вектора Y, а матрица диффузии B(Y,t) не зависит от вектора Y. Применение вектора развито в работах Пугачева В.С.
5. Метод функциональных (степенных) рядов применим при постоянных коэффициентов диффузии. Коэффициенты сноса аппроксимируются степенными рядами.
Метод является приближенным и применим к частному виду динамических систем.
Из приведенного краткого обзора методов интегрирования уравнения ФПК следует, что общие алгоритмы решения сложны и не могут быть применены ко всем задачам.
Поэтому целесообразна разработка приближенных методов, дающих решение для систем общего нестационарного нелинейного вида.
Рассмотрим основные из них.
6. Метод гауссовой аппроксимации основан на возможности замены любой искомой функции плотности вероятности нормальной (гауссовой) функцией с совпадающими векторами математического ожидания и корреляционной матрицей.
При этом решаются уравнения для моментов my и θy.
Функция ω1(Y,t) – многомерная гауссова плотность вероятности имеет вид
 , (20)
, (20)
где ∆ - определитель, соответствующий корреляционной матрице θ.
 . (21)
. (21)
∆* - окаймленный определитель вида
 или
или  . (22)
. (22)
7.Метод ортогонального разложения – аппроксимация многомерной функции ω1(Y,t) c точностью до совпадения моментов первого mi(t) и второго θij порядков разработан Мальчиковым С.В.
При этом многомерная функция представляется в форме
 , (23)
, (23)
где ω1r(yr,t) – одномерная функция плотности вероятности координаты yr (r = 1,…,n).
При такой аппроксимации совпадают вектор математического ожидания m и матрица корреляционных моментов θ.
Приближенным методом решением уравнения ФПК является также численное решение с помощью итерационной процедуры при дискретизации процесса Y(t).
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...