
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
III. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ
III. ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ
ПЕРЕМЕННОЙ И ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Комплексные числа и действия над ними
Алгебраическая форма комплексных чисел
Комплексными числами называются упорядоченные пары  действительных чисел
действительных чисел  и
и  , для которых введены понятия равенства и операции сложения и умножения:
, для которых введены понятия равенства и операции сложения и умножения:
 если
если  , (1)
, (1)
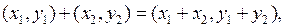 (2)
(2)
 . (3)
. (3)
Из формул (2) и (3) вытекают, в частности, соотношения

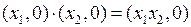 ,
,
которые показывают, что операции над комплексными числами вида 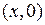 совпадают с операциями над действительными числами
совпадают с операциями над действительными числами  . Поэтому комплексные числа вида
. Поэтому комплексные числа вида 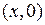 отождествляются с действительными числами:
отождествляются с действительными числами:  . Особую роль играет число
. Особую роль играет число  , которое называется мнимой единицей.
, которое называется мнимой единицей.
Из формул (2), (3) вытекают также равенства
 ,
,
 ,
,
 .
.
Итак, каждое комплексное число  можно представить в виде
можно представить в виде 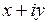 . Такая запись комплексного числа называется алгебраической формой комплексного числа. Число
. Такая запись комплексного числа называется алгебраической формой комплексного числа. Число  называется действительной частью, а
называется действительной частью, а  – мнимой частью комплексного числа
– мнимой частью комплексного числа 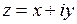 . Для них приняты следующие обозначения:
. Для них приняты следующие обозначения:
 .
.
Комплексное число  называется сопряженным с комплексным числом
называется сопряженным с комплексным числом 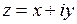 .
.
Число  называется модулем комплексного числа
называется модулем комплексного числа 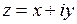 . Очевидно,
. Очевидно,  , причем,
, причем,  , тогда и только тогда, когда
, тогда и только тогда, когда  . Модуль действительного числа совпадает с абсолютной величиной этого числа.
. Модуль действительного числа совпадает с абсолютной величиной этого числа.
Отметим две формулы:  ,
,  , которые вытекают из определений
, которые вытекают из определений  и равенства
и равенства
 .
.
Вычитание и деление комплексных чисел являются действиями, обратными соответственно сложению и умножению.
Если  ,
,  ,
,
то 
 .
.
Пример 1.Найти сумму, разность, произведение и частное двух комплексных чисел 
Решение.  ,
,
 ,
,


Функции комплексного переменного
Примеры
 Функция
Функция  .
.
Здесь  ,
,  .
.
 Функция
Функция 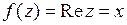 . Здесь
. Здесь  ,
,  .
.

 – многочлен степени
– многочлен степени  с комплексными коэффициентами.
с комплексными коэффициентами.
 Рациональная функция
Рациональная функция  где
где  и
и  – многочлены.
– многочлены.
 Учитывая формулы Эйлера, функции sin z и cos z для любого комплексного z определим равенствами
Учитывая формулы Эйлера, функции sin z и cos z для любого комплексного z определим равенствами
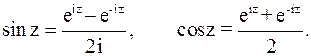
Отметим, что все формулы элементарной тригонометрии, справедливые для действительных x, остаются справедливыми и при всех комплексных значениях z. Кроме того, можно доказать, что уравнения  и
и  имеют решения только при
имеют решения только при  то есть только на действительной оси. Следовательно, все решения уравнения
то есть только на действительной оси. Следовательно, все решения уравнения  находятся по формуле
находятся по формуле  а все решения уравнения
а все решения уравнения  определяются формулой
определяются формулой 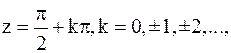
 Функции tgz и ctg z для любого комплексного z определим формулами
Функции tgz и ctg z для любого комплексного z определим формулами

 Функции shz, chz и
Функции shz, chz и  для любого комплексного z определим равенствами
для любого комплексного z определим равенствами 

Из определения видно, что  =
= 
 Таким образом, свойства функций
Таким образом, свойства функций  и
и  непосредственно вытекают из свойств функций sinz, cosz и
непосредственно вытекают из свойств функций sinz, cosz и  Отметим в частности, что все решения уравнения
Отметим в частности, что все решения уравнения  находятся по формуле
находятся по формуле  а все решения уравнения
а все решения уравнения  определяются формулой
определяются формулой  . Кроме того, функции
. Кроме того, функции  и
и  непрерывны на всей комплексной плоскости, а функция
непрерывны на всей комплексной плоскости, а функция  непрерывна при
непрерывна при  , где
, где 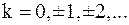
Аналитические функции
Понятие предела и производной для функции комплексного переменного вводятся так же, как и для функции действительного переменного.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  Скажем, что существует предел
Скажем, что существует предел  если существуют пределы
если существуют пределы  и
и  ; при этом будем полагать
; при этом будем полагать 
Если существует конечный предел
 ,
,
то этот предел называют производной функции 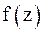 в точке
в точке  и обозначают
и обозначают  а функцию
а функцию 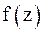 называют дифференцируемой в точке
называют дифференцируемой в точке 
Имеет место теорема: для того чтобы функция  , определенная в области
, определенная в области  , была дифференцируема в точке
, была дифференцируема в точке 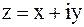 этой области, необходимо и достаточно, чтобы функции
этой области, необходимо и достаточно, чтобы функции  и
и  были дифференцируемы в той же точке (как функции двух переменных
были дифференцируемы в той же точке (как функции двух переменных  ) и чтобы, кроме того, в этой точке выполнялись условия Коши-Римана:
) и чтобы, кроме того, в этой точке выполнялись условия Коши-Римана:
 ;
;  .
.
При выполнении условий теоремы производная  может быть представлена в одной из следующих форм:
может быть представлена в одной из следующих форм:

Функция  , дифференцируемая в каждой точке области
, дифференцируемая в каждой точке области  , называется дифференцируемой в этой области, или аналитической.
, называется дифференцируемой в этой области, или аналитической.
Примеры
 Функция
Функция  является аналитической на всей комплексной плоскости. В самом деле,
является аналитической на всей комплексной плоскости. В самом деле,  ;
;
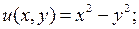



 Функция
Функция  не является аналитической на комплексной плоскости. Действительно, здесь
не является аналитической на комплексной плоскости. Действительно, здесь  ,
, 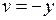 ,
,  ,
,  ,
,  .
.
Пользуясь условиями Коши-Римана, можно восстановить аналитическую функцию, если известна ее действительная часть  или мнимая часть
или мнимая часть  и, кроме того, задано значение
и, кроме того, задано значение  функции в некоторой точке
функции в некоторой точке  .
.
Пример.Восстановить аналитическую функцию  , если дана ее действительная часть
, если дана ее действительная часть  ,
,  .
.
Решение.В силу условий Коши-Римана имеем
 , (1)
, (1)
 . (2)
. (2)
Интегрируя уравнение (2) по переменной  , находим мнимую часть
, находим мнимую часть  . Слагаемое
. Слагаемое  является постоянной (относительно
является постоянной (относительно  ) интегрирования. Дифференцируя последнее равенство по
) интегрирования. Дифференцируя последнее равенство по  , и сравнивая результат с уравнением (1), получаем
, и сравнивая результат с уравнением (1), получаем
 , откуда
, откуда
 и
и  .
.
Следовательно,  и
и  , то есть
, то есть  . Учитывая дополнительное условие
. Учитывая дополнительное условие  , получим:
, получим:  , откуда
, откуда  . Итак,
. Итак, 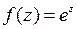 .
.
Ряды
Ряд Тейлора
Справедливы следующие теоремы.
1. Всякую функцию  , аналитическую в круге с центром в точке
, аналитическую в круге с центром в точке  можно представить внутри этого круга в виде суммы ряда Тейлора:
можно представить внутри этого круга в виде суммы ряда Тейлора:

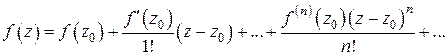 (1)
(1)
Во всякой замкнутой области, принадлежащей этому кругу, ряд Тейлора (1) сходится равномерно.
2. Всякую аналитическую функцию в каждой внутренней точке области аналитичности можно разложить в ряд Тейлора (1). Это разложение справедливо в области  , где
, где 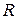 – расстояние от точки
– расстояние от точки 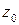 до ближайшей особой точки функции
до ближайшей особой точки функции  , то есть точки, в которой
, то есть точки, в которой  не является аналитической.
не является аналитической.
3. Если функция  разлагается в окрестности точки
разлагается в окрестности точки 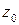 в степенной ряд
в степенной ряд  , то этот ряд является ее рядом Тейлора, то есть
, то этот ряд является ее рядом Тейлора, то есть
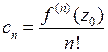 ,
,  .
.
Пользуясь теоремой 3, можно разложить данную функцию  в ряд по степеням
в ряд по степеням  , который является ее рядом Тейлора в окрестности точки
, который является ее рядом Тейлора в окрестности точки 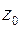 . Часто коэффициенты такого ряда находят, используя известные разложения функций
. Часто коэффициенты такого ряда находят, используя известные разложения функций 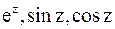 и т.д.
и т.д.
Напомним также разложение
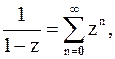 (2)
(2)
сходящееся в круге 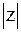 <1.
<1.
Пример 1.Разложить функцию 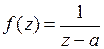 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 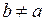 . Указать область, в которой справедливо это разложение.
. Указать область, в которой справедливо это разложение.
Решение.В окрестности точки 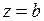 функция
функция 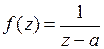 является аналитической. Следовательно, согласно теореме 2, ее можно разложить в ряд Тейлора. Для разложения в ряд Тейлора преобразуем данную функцию к виду
является аналитической. Следовательно, согласно теореме 2, ее можно разложить в ряд Тейлора. Для разложения в ряд Тейлора преобразуем данную функцию к виду
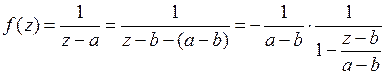 .
.
Разложим второй сомножитель в ряд по формуле (2). Область сходимости этого ряда  , отсюда
, отсюда  .
.
Искомое разложение имеет вид:
 ,
,
или
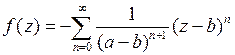 ;
; 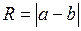 .
.
Пример 2. Разложить функцию 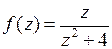 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 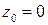 . Указать область, в которой справедливо это разложение.
. Указать область, в которой справедливо это разложение.
Решение.Для разложения в ряд Тейлора преобразуем данную функцию к виду 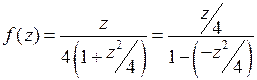 и воспользуемся формулой (2).
и воспользуемся формулой (2).
Так как  , то
, то  . Получаем искомое разложение:
. Получаем искомое разложение:
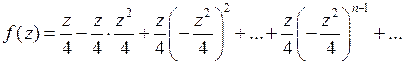 ,
,
 ;
; 
Ряд Лорана
Справедлива теорема:
Функция  , аналитичная в кольце
, аналитичная в кольце  , представляется в этом кольце сходящимся рядом Лорана
, представляется в этом кольце сходящимся рядом Лорана
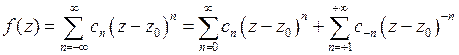 , (3)
, (3)
где
 , (4)
, (4)
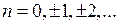 ,
, 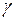 – любая окружность, ориентированная против часовой стрелки и лежащая внутри указанного кольца с центром в точке
– любая окружность, ориентированная против часовой стрелки и лежащая внутри указанного кольца с центром в точке  . Разложение в ряд Лорана единственно.
. Разложение в ряд Лорана единственно.
Первое слагаемое в разложении (3) называется правильной частью ряда Лорана, второе слагаемое – главной частью ряда Лорана. Правильная часть ряда Лорана сходится в круге 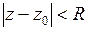 . Главная часть ряда Лорана сходится во внешности круга радиуса
. Главная часть ряда Лорана сходится во внешности круга радиуса 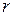 , то есть при
, то есть при  .
.
Разложение (3) иногда можно получить на практике, не применяя формулы (4) для коэффициентов 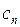 .
.
Пример 1. Найти все разложения функции  в ряд Лорана по степеням
в ряд Лорана по степеням  .
.
Решение.Пусть 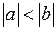 . Тогда данная функция может быть разложена в ряд Лорана в кольцах:
. Тогда данная функция может быть разложена в ряд Лорана в кольцах:
I) 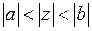 , II)
, II) 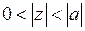 , III)
, III) 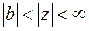 ,
,
где она является аналитической.
Разлагаем  на элементарные дроби:
на элементарные дроби:
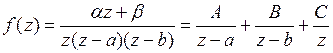 .
.
I. Дробь  разлагается вне круга
разлагается вне круга 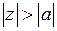 по степеням
по степеням  с отрицательными показателями, то есть
с отрицательными показателями, то есть
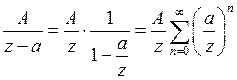 , при
, при  .
.
Дробь 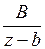 разлагается внутри круга
разлагается внутри круга 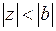 по степеням
по степеням  с положительными показателями, то есть
с положительными показателями, то есть
 , при
, при 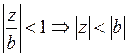 .
.
Итак,  , при
, при 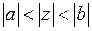 .
.
II. Дроби  и
и 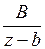 разложим в ряд по степеням
разложим в ряд по степеням  с положительными показателями внутри круга
с положительными показателями внутри круга 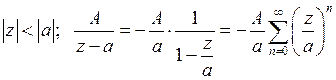 ,
,
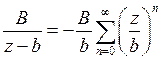 ,
, 
Итак, 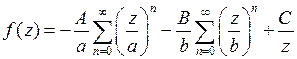 , при
, при 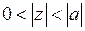 .
.
III. Дроби  и
и 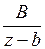 разложим по степеням
разложим по степеням  с отрицательными показателями, то есть
с отрицательными показателями, то есть
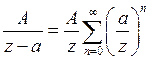 , где
, где 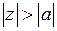 ;
; 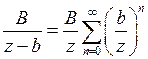 , где
, где  .
.
Итак,  ,
,  .
.
Пример 2.Найти все лорановские разложения  по степеням
по степеням  , если
, если 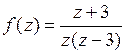 ,
,  .
.
Решение.Пусть 
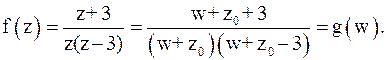
Точки 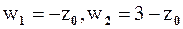 являются особыми точками функции
являются особыми точками функции 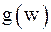 (в них
(в них 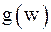 не аналитична). Тогда кольцами аналитичности
не аналитична). Тогда кольцами аналитичности 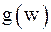 будут области:
будут области: 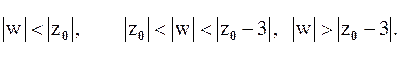
Возвращаясь к переменной 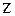 , получаем следующие области разложения
, получаем следующие области разложения  по степеням
по степеням 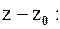

Рассмотрим разложение функции  в ряд Лорана в кольце
в ряд Лорана в кольце 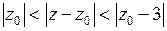 , то есть
, то есть 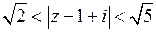 .
.
Представим функцию  в виде
в виде
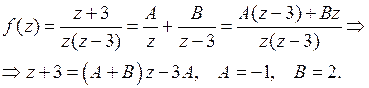

Таким образом,  .
.
Дробь 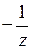 разложим по степеням
разложим по степеням  с отрицательными показателями вне круга
с отрицательными показателями вне круга  , то есть
, то есть
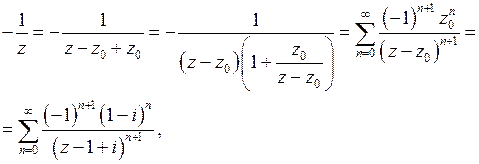
где 
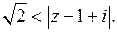
Дробь 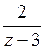 разложим по степеням
разложим по степеням  с положительными показателями внутри круга
с положительными показателями внутри круга  , то есть
, то есть

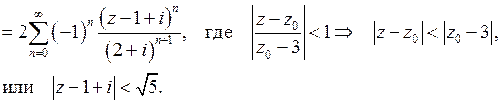
Итак,  ,
,
где  .
.
Остальные случаи разложения данной функции в ряд Лорана предлагается рассмотреть самостоятельно.
Для разложения функции в ряд Лорана иногда используют готовые разложения элементарных функций в ряд Тейлора.
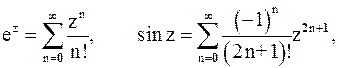


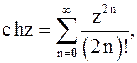 (5)
(5)
которые сходятся во всей комплексной плоскости.
Пример 3.Функцию 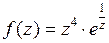 разложить в ряд Лорана в окрестности точки
разложить в ряд Лорана в окрестности точки 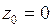 .
.
Решение.Функция  является аналитической в кольце
является аналитической в кольце 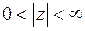 . Следовательно, она разложима в ряд Лорана. Воспользуемся разложением функции
. Следовательно, она разложима в ряд Лорана. Воспользуемся разложением функции  в ряд Тейлора
в ряд Тейлора 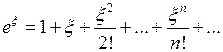 .
.
и положим 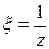 :
:
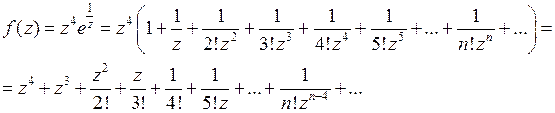 (6)
(6)
В силу единственности разложения в ряд Лорана (6) является рядом Лорана для функции  в кольце
в кольце 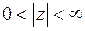 .
.
Изолированные особые точки
Точка  называется изолированной особой точкой функции
называется изолированной особой точкой функции 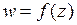 , если
, если  аналитична в кольце
аналитична в кольце  , но не определена в точке
, но не определена в точке 
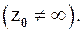
Если  – изолированная особая точка функции
– изолированная особая точка функции  , то эту функцию можно разложить в ряд Лорана (3), который сходится к ней в кольце
, то эту функцию можно разложить в ряд Лорана (3), который сходится к ней в кольце 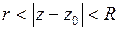 , где
, где 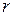 – сколь угодно малое положительное число, а
– сколь угодно малое положительное число, а 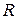 – расстояние от точки
– расстояние от точки  до другой особой точки функции
до другой особой точки функции  .
.
Изолированная особая точка  называется устранимой, если разложение (3) не содержит степеней разности
называется устранимой, если разложение (3) не содержит степеней разности 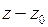 с отрицательными показателями, то есть
с отрицательными показателями, то есть
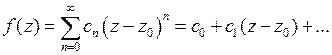 .
.
Точка  является устранимой особой точкой функции
является устранимой особой точкой функции  в том и только том случае, если функция
в том и только том случае, если функция  ограничена в некоторой окрестности точки
ограничена в некоторой окрестности точки  .
.
Пример 1.Функция 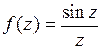 имеет изолированную особую точку
имеет изолированную особую точку 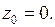 Чтобы найти разложение в ряд Лорана
Чтобы найти разложение в ряд Лорана  в окрестности точки
в окрестности точки 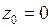 , воспользуемся формулой (5).
, воспользуемся формулой (5).
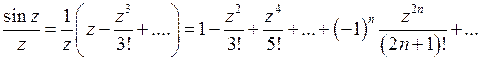 .
.
Это разложение не содержит степеней  с отрицательными показателями. Следовательно, точка
с отрицательными показателями. Следовательно, точка 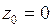 – устранимая особая точка.
– устранимая особая точка.
Изолированная особая точка  называется полюсом, если разложение (3) содержит конечное число
называется полюсом, если разложение (3) содержит конечное число  степеней разности
степеней разности 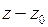 с отрицательными показателями, при этом число
с отрицательными показателями, при этом число  называется порядком полюса.
называется порядком полюса.
Для определения порядка полюса функции  можно использовать теорему.
можно использовать теорему.
Для того, чтобы точка  являлась полюсом порядка
являлась полюсом порядка 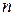 функции
функции  , необходимо и достаточно, чтобы функцию
, необходимо и достаточно, чтобы функцию  можно было представить в виде
можно было представить в виде
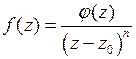 , (7)
, (7)
где  – аналитическая функция в окрестности точки
– аналитическая функция в окрестности точки  и
и 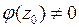 .
.
Полюса и нули аналитических функций связаны друг с другом.
Нулём функции  называют любую точку
называют любую точку 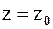 , в которой
, в которой  Разлагая аналитическую функцию в ряд Тейлора (1) в окрестности нуля, получим:
Разлагая аналитическую функцию в ряд Тейлора (1) в окрестности нуля, получим:
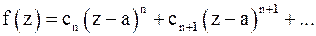 , (8)
, (8)
где  и
и  Число n называют порядком нуля аналитической функции
Число n называют порядком нуля аналитической функции 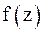 в точке
в точке  . Из (8) следует, что в окрестности нуля порядка n аналитическая функция
. Из (8) следует, что в окрестности нуля порядка n аналитическая функция 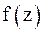 допускает представление
допускает представление
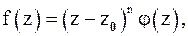 (9)
(9)
где  . Кроме того, порядок нуля можно определить следующим образом.
. Кроме того, порядок нуля можно определить следующим образом.
Если 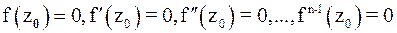 , а
, а 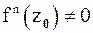 , то порядок нуля аналитической функции
, то порядок нуля аналитической функции 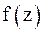 в точке
в точке  равен n.
равен n.
Справедливо утверждение.
Если аналитическую функцию  можно представить в виде
можно представить в виде  , где аналитические функции
, где аналитические функции  и
и 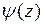 имеют в точке
имеют в точке  нули порядка k и m соответственно,
нули порядка k и m соответственно, 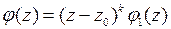 и
и 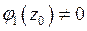 ,
,  и
и  ,то в точке
,то в точке  функция
функция  имеет полюс порядка
имеет полюс порядка 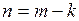 , при
, при  ; устранимую особую точку при
; устранимую особую точку при  .
.
В частности, если  а
а 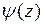 имеет в этой точке нуль порядка
имеет в этой точке нуль порядка 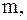 то
то  имеет в точке
имеет в точке  полюс порядка
полюс порядка 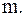 То есть в этом случае порядок полюса функции
То есть в этом случае порядок полюса функции  совпадает с порядком нуля знаменателя.
совпадает с порядком нуля знаменателя.
Изолированная особая точка  называется существенно особой, если разложение (3) содержит бесконечное множество степеней
называется существенно особой, если разложение (3) содержит бесконечное множество степеней 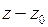 с отрицательными показателями.
с отрицательными показателями.
Пример 2.Найти все особые точки функций  , определить их тип.
, определить их тип.
1. 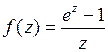 . 2.
. 2.  . 3.
. 3.  .
.
4. 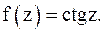
Решение.1. Чтобы найти разложение в ряд Лорана функции 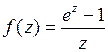 в окрестности точки
в окрестности точки 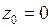 , воспользуемся формулой (5). Получим:
, воспользуемся формулой (5). Получим:
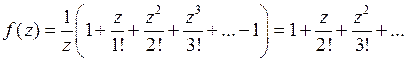 ,
,
Так как полученный ряд не содержит степеней  с отрицательными показателями, то точка
с отрицательными показателями, то точка 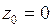 является устранимой особой точкой.
является устранимой особой точкой.
2. Функция  имеет две изолированные особые точки
имеет две изолированные особые точки 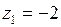 и
и  . Определим их тип. Пусть
. Определим их тип. Пусть 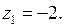 Представим функцию в виде
Представим функцию в виде 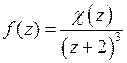 , где
, где  ,
,  .
.
Тогда, согласно (7), 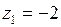 есть полюс порядка
есть полюс порядка 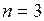 .
.
Пусть  Представим функцию
Представим функцию 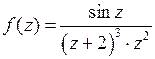 в виде
в виде  , где
, где 
 Так как
Так как 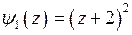 при
при 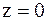 ,
,  то порядок нуля знаменателя
то порядок нуля знаменателя  .
.
Для 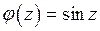 имеем:
имеем: 

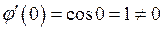 , откуда следует, что
, откуда следует, что  имеет ноль первого порядка, то есть
имеет ноль первого порядка, то есть 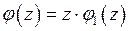 и
и 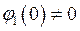 .
.
Следовательно, точка  есть полюс порядка
есть полюс порядка 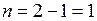 , то есть простой полюс.
, то есть простой полюс.
3. Функция  имеет изолированную особую точку
имеет изолированную особую точку  Подставим в разложение в ряд Тейлора (5) функции
Подставим в разложение в ряд Тейлора (5) функции 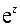 вместо z выражение
вместо z выражение 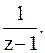 Получим разложение
Получим разложение 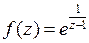 в окрестности особой точки
в окрестности особой точки 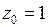
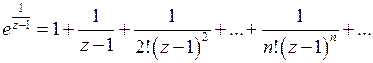 .
.
Этот ряд содержит бесконечное множество степеней 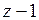 с отрицательными показателями; следовательно,
с отрицательными показателями; следовательно, 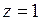 – существенно особая точка.
– существенно особая точка.
4. Для функции 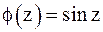 точки
точки 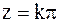 (k – целое число) являются нулями первого порядка, так как
(k – целое число) являются нулями первого порядка, так как 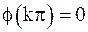 ,
, 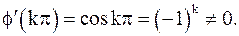 Тогда для
Тогда для 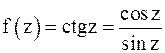 точки
точки 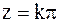 являются полюсами первого порядка (см. (7)), так как
являются полюсами первого порядка (см. (7)), так как 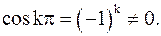
Бесконечно удаленную точку 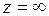 называют изолированной особой точкой функции
называют изолированной особой точкой функции 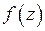 , если в некоторой ее окрестности (то есть вне круга с центром в точке
, если в некоторой ее окрестности (то есть вне круга с центром в точке 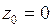 достаточно большого радиуса) нет других особых точек функции
достаточно большого радиуса) нет других особых точек функции 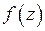 . Для изучения поведения функции
. Для изучения поведения функции 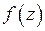 в окрестности точки
в окрестности точки 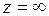 полагают
полагают 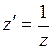 . Тогда окрестность точки
. Тогда окрестность точки 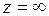 перейдет в окрестность точки
перейдет в окрестность точки 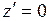 и
и  . Если
. Если 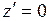 является устранимой, полюсом или существенно особой точкой для функции
является устранимой, полюсом или существенно особой точкой для функции  , то
, то 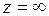 считают, соответственно, устранимой, полюсом или существенно особой точкой функции
считают, соответственно, устранимой, полюсом или существенно особой точкой функции 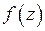 .
.
Можно показать, что точка 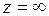 будет устранимой, полюсом или существенно особой точкой функции
будет устранимой, полюсом или существенно особой точкой функции 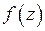 , если ряд Лорана для
, если ряд Лорана для 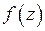 в этой точки окрестности не содержит степеней
в этой точки окрестности не содержит степеней  с положительными показателями, содержит их в конечном числе или бесконечное множество соответственно.
с положительными показателями, содержит их в конечном числе или бесконечное множество соответственно.
Пример 3.Исследовать поведение функции 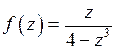 в окрестности бесконечно удаленной точки.
в окрестности бесконечно удаленной точки.
Решение.Введем переменную 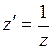 . Тогда
. Тогда
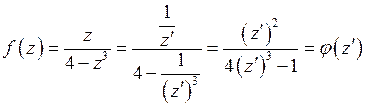 .
.
Так как 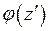 ограничена в окрестности точки
ограничена в окрестности точки 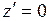 ,
, 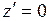 является устранимой особой точкой для
является устранимой особой точкой для 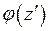 , то и точка
, то и точка 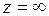 также является устранимой особой точкой для функции
также является устранимой особой точкой для функции 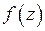 .
.
Пример 4. Исследовать поведение функции  в окрестности бесконечно удаленной точки.
в окрестности бесконечно удаленной точки.
Решение. Разложим данную функцию в ряд Лорана. Для этого подставим в разложение в ряд Тейлора (5) функции 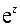 вместо z выражение
вместо z выражение 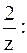

Это разложение содержит конечное число степеней  с положительными показателями, причем наивысший показатель степени
с положительными показателями, причем наивысший показатель степени  . Поэтому точка
. Поэтому точка 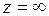 является полюсом второго порядка для функции
является полюсом второго порядка для функции 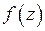 .
.
Теорема аналитичности
Для всякого оригинала  изображение
изображение  определено в полуплоскости
определено в полуплоскости  , где
, где
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...