
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Теорема о дифференцировании по параметру
Если при любом  оригиналу
оригиналу  соответствует изображение
соответствует изображение  , то
, то  .
.
Теорема о дифференцировании оригинала
Если  ,
,  являются функциями-оригиналами и
являются функциями-оригиналами и  , то
, то  .
.
 ,
,
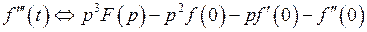 и, вообще,
и, вообще,
 ,
,
где под  понимается правое предельное значение
понимается правое предельное значение  .
.
Теорема о дифференцировании изображения
Если  является оригиналом и
является оригиналом и  , то
, то  , то есть дифференцирование изображения сводится к умножению оригинала на
, то есть дифференцирование изображения сводится к умножению оригинала на 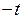 . Вообще,
. Вообще,  , где
, где  – натуральное число.
– натуральное число.
Интегрирование оригинала
Если  является оригиналом и
является оригиналом и  , то
, то  , то есть интегрирование оригинала в пределах от
, то есть интегрирование оригинала в пределах от 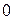 до
до  приводит к делению изображения на
приводит к делению изображения на  .
.
Интегрирование изображения
Если  является оригиналом,
является оригиналом,  и
и  сходится, то
сходится, то 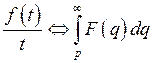 , то есть интегрирование изображения от
, то есть интегрирование изображения от  до
до  соответствует делению оригинала на
соответствует делению оригинала на  .
.
Умножение изображений
Если  и
и  являются оригиналами,
являются оригиналами,  и
и  , то выражению
, то выражению  , называемому сверткой функций
, называемому сверткой функций  и
и  , соответствует произведение изображений, то есть
, соответствует произведение изображений, то есть  .
.
Существенное значение имеет так называемые формулы Дюамеля:




 .
.
При нахождении изображений по оригиналам и оригиналов по изображениям, удобно пользоваться формулами соответствия, которые приведены в следующей таблице:
| Номер формулы | Оригинал | Изображение |
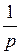
| ||

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |

| 
| |
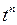
| 
|
7.2. Нахождение изображения по оригиналу
Задачу о нахождении изображения по оригиналу можно решать, используя таблицу соответствия и свойства преобразования Лапласа.
Пример 1.  . Найти
. Найти  .
.
Решение. Используя теорему линейности и формулы (1-4) таблицы соответствия, получим
 .
.
Пример 2.  . Найти
. Найти  .
.
Решение.  .
.

Используя теорему линейности, теорему затухания и формулу (8) таблицы соответствия, получим
 .
.
Пример 3.  . Найти
. Найти  .
.
Решение. 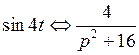 .
.
Используя теорему об интегрировании изображения, находим

Пример 4.  . Найти
. Найти  .
.
Решение.  Используя теорему о дифференцировании изображения, находим
Используя теорему о дифференцировании изображения, находим

Если функция  задана разными выражениями на разных промежутках, то ее надо предварительно представить в виде
задана разными выражениями на разных промежутках, то ее надо предварительно представить в виде  , где
, где  – функция Хэвисайда, а затем воспользоваться теоремой запаздывания.
– функция Хэвисайда, а затем воспользоваться теоремой запаздывания.
Пример 5.Найти изображение функции

Решение.Представим  в виде
в виде  .
.
Имеем  ;
;  . Используя свойство линейности, получим
. Используя свойство линейности, получим  .
.
Пример 6.Найти  , если оригинал
, если оригинал  задан графиком:
задан графиком:

Решение
В аналитической форме 
Заметим, что на интервале  уравнение прямой найдено по формуле
уравнение прямой найдено по формуле
 .
.
Рассмотрим функции 

Тогда 
 (см. пример 5).
(см. пример 5).
Поступая аналогично, получим

Нахождение оригинала по изображению
В общем случае нахождение оригинала по изображению достигается использованием теоремы обращения:
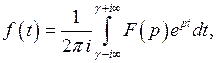
 . (1)
. (1)
Однако для произвольных  это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения
это приводит к большим трудностям. Мы рассмотрим несколько удобных приемов нахождения  в предположении, что
в предположении, что  отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе. Разложив
отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе. Разложив  на простейшие дроби, получим
на простейшие дроби, получим
 ,
,
где  – комплексные числа,
– комплексные числа, 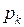 – нули знаменателя
– нули знаменателя  ,
,  – их порядок. Пользуясь формулой 10 таблицы соответствия и теоремой линейности, легко получить
– их порядок. Пользуясь формулой 10 таблицы соответствия и теоремой линейности, легко получить
 и
и  .
.
Часто бывает удобнее разложить изображение на простейшие дроби вида
 ,
,  ,
,  .
.
При этом также можно использовать формулы таблицы соответствия.
Пример 1.  .Найти
.Найти  .
.
Решение. Разложим дробь  на простейшие дроби:
на простейшие дроби:
 ,
,
 .
.
Полагая  , получим
, получим  , при
, при 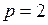 , получим
, получим  , при
, при  , имеем
, имеем  .
.
 .
.
Используя теорему линейности и таблицу соответствия (формулы 2,10), получим
 .
.
При нахождении  по
по  иногда целесообразно использовать теорему о произведении изображений (теорему о свертке).
иногда целесообразно использовать теорему о произведении изображений (теорему о свертке).
Пример 2. 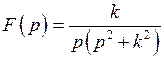 .Найти
.Найти  .
.
Решение
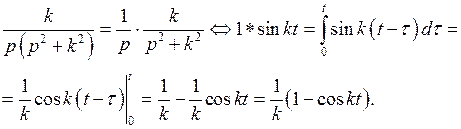
В некоторых случаях удобно использовать формулу Дюамеля.
Пример 3.  .Найти
.Найти  .
.
Решение.  ;
;
 ;
;  .
.
По формуле Дюамеля имеем
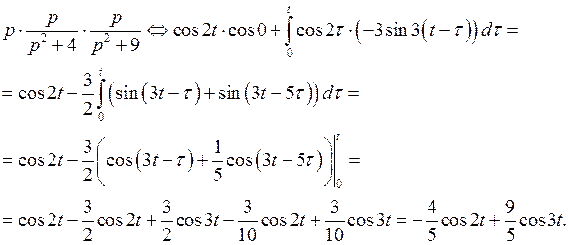
Можно находить  по
по  , используя теорию вычетов (теорему разложения, которая выводится из (1)). А именно: если
, используя теорию вычетов (теорему разложения, которая выводится из (1)). А именно: если  отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе, то
отношение двух многочленов, причем степень многочлена стоящего в знаменателе больше степени многочлена стоящего в числителе, то
 (2)
(2)
где 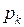 – полюса функции
– полюса функции  .
.
Пример 4.  .Найти оригинал.
.Найти оригинал.
Решение. Функция  имеет два полюса:
имеет два полюса:  – полюс второго порядка и
– полюс второго порядка и  – полюс первого порядка. По формуле (2)
– полюс первого порядка. По формуле (2)
 .
.
Находим вычеты: 
 .
.
 .
.
Если все полюса  функции
функции  первого порядка,
первого порядка, 

 то формула
то формула  принимает вид
принимает вид
 ,
,
где сумма берется по всем корням  .
.
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...