Пересечение поверхности с плоскостью

Это есть позиционная задача на определение для данных геометрических объектов их общего элемента, которым является кривая линия.

Для её построения используются вспомогательные плоскости-посредники частного положения, одновременно пересекающие данные поверхность и плоскость.

Построение линии b пересечения фронтально проецирующей плоскости Q с поверхностью закрытого тора выполнено в соответствии с рисунком 1.3.48. Для этого введён ряд вспомогательных горизонтальных плоскостей –посредников Г(Г₂), Г¢(Г¢₂), Г¢(Г¢₂) и т.д. Плоскость Г(Г₂) пересекает поверхность закрытого тора по окружностям l(l₁,l₂), а плоскость Q она пересекает по фронтально проецирующей прямой (3-3¢). Проекции этой прямой на чертеже обозначены следующим образом: горизонтальная – (3₁-3¢₁) и фронтальная – (3₂º3¢₂). Точки 3 и 3¢ в силу проецирующего положения плоскости Q являются одновременно и точками линии b как линии пересечения плоскости Q с данной поверхностью закрытого тора. Все другие точки линии b определяются аналогично точкам 3 и 3¢ при помощи плоскостей-посредников Г¢, Г¢ и т.д. Проекции линии b на чертеже обозначены следующим образом: фронтальная – b₂ºQ₂ и горизонтальная – b₁, представляющая собой плавную кривую, соединяющую точки 3, 3¢ и т.д. Следует заметить, что при построении линии b в первую очередь надо отметить точки 1 и 2 как опорные. Положение этих точек при данном расположении на чертеже поверхности закрытого тора и плоскости Q определяется наличием общей плоскости симметрии S(S₁), которая является плоскостью главного меридиана поверхности закрытого тора. Действительно, плоскостью симметрии плоскости Q(Q₂) будет вообще любая плоскость, к ней перпендикулярная, а плоскостью симметрии поверхности будет всякая плоскость, проходящая через её ось. Общая плоскость симметрии должна удовлетворять обоим указанным условиям и очевидно, что такой плоскостью будет S(S₁). В силу этого линия b тоже симметрична относительно плоскости S, а её горизонтальная проекция симметрична относительно следа плоскости S₁. Точки 1 и 2 лежат на главном меридиане поверхности. Отметив их фронтальные проекции 1₂ и 2₂, найдём горизонтальные проекции этих точек (1₁ и 2₁) на горизонтальной проекции главного меридиана.

Построение линии пересечения гранной поверхности с плоскостью выполнено в соответствии с рисунком 1.3.49.

Сечение многогранника может быть ограничено только отрезками прямых. Число сторон такого многогранника равно числу граней многогранника, пересекаемых плоскостью. Вершинами многоугольника сечения являются точки пересечения рёбер многогранника с секущей плоскостью. Следовательно, число вершин многоугольника равно числу рёбер многогранника, пересекаемых плоскостью.

Рисунок 1.3.48 – Пересечение плоскости с поверхностью закрытого тора

Рисунок 1.3.49 – Пересечение гранной поверхности с плоскостью

Следует заметить, что вершинами многоугольника сечения являются точки пересечения секущей плоскости с рёбрами многогранника в собственном смысле. Это значит, что точки пересечения секущей плоскости с продолжением рёбер не могут являться вершинами многоугольника сечения как не принадлежащие поверхности многогранника, но могут быть использованы для удобства построения.

Аналогично, сторонами многоугольника сечения могут являться только те отрезки прямых, которые принадлежат граням в собственном смысле.

В данном примере пирамида пересекается с фронтально проецирующей плоскостью S(S₁). Решение получается простым, поскольку фронтальная проекция сечения вырождается в отрезок прямой линии, совпадающей с фронтальным следом плоскости S. Горизонтальной проекцией сечения является пятиугольник с вершинами 1₁, 2₁, 4₁, 5₁, 3₁.

Конические сечения

Линии, которые получаются при пересечении поверхности конуса второго порядка с плоскостью, называются коническими сечениями.

К этим линиям относятся следующие: эллипс,парабола,гипербола,окружность,две прямые.

Рисунок 1.3.50 – Конические сечения

Если секущая плоскость S¹(S¹₂) пересекает все образующие конуса, то в сечении получается эллипс.

Если секущая плоскость S(S₂) перпендикулярна к оси вращения конуса, то в сечении получается окружность.

Если секущая плоскость S²(S²₂) параллельна одной образующей конуса, то в сечении будет парабола.

Если секущая плоскость S³(S³₂) параллельна двум образующим конуса, то получим гиперболу.

Гипербола может быть получена и в случае расположения секущей плоскости S⁴(S⁴₂) параллельно оси конуса. В этом случае плоскость параллельна двум образующим, проекции которых совпадают с проекцией оси.

Две прямые в сечении получаются, если секущая плоскость S⁵(S⁵₂) проходит через вершину конуса.

Пример построения сечения конуса по параболе показан на рисунке 2.3.51. При построении сначала определялись опорные (экстремальные) точки 1, 2, и 2¢. Затем определялись промежуточные точки с помощью горизонтальных плоскостей-посредников Г(Г₂). Их построение можно видеть на примере точек 3 и 3¢.

Рисунок 1.3.51 – Сечение конуса по параболе

Пересечение поверхностей

Построение линий пересечения поверхностей, как и построение точки пересечения линии с поверхностью, означает определение их общих элементов. Такие задачи относят к позиционным. При их решении не учитываются метрические свойства объектов, которые могут быть выявлены лишь в результате измерения.

Линию пересечения двух поверхностей находят с помощью приёма, который называется способом вспомогательных секущих поверхностей-посредников.

Общий алгоритм решения задачи

Пусть даны две произвольные поверхности Ф и Q. Нужно построить линию их пересечения, т.е. построить точки, которые этой линии принадлежат (рисунок 1.3.52).

Чтобы построить такие точки, надо данные поверхности пересечь одновременно некоторой вспомогательной поверхностью Г. Следующим действием является построение линий пересечения поверхности-посредника Г с каждой из данных поверхностей:

l = Г ∩ Ф,

m = Г ∩Q .

Рисунок 1.3.52 – Пересечение двух поверхностей

Затем отмечаем точки пересечения полученных линий как лежащих на поверхности-посреднике:

А = l ∩ m,

B = l ∩ m и т.д.

Эти точки принадлежат и поверхности Г, и данным поверхностям Ф, Q, и поэтому они принадлежат искомой линии пересечения поверхностей Ф и Q.

Повторяя приём, можно найти такое количество точек кривой, которое позволяет достаточно точно провести через эти точки искомую кривую по лекалу.

Введение поверхности-посредника позволяет свести задачу о пересечении двух кривых поверхностей к более простой задаче пересечения двух линий, лежащих на одной вспомогательной поверхности.

Вид и расположение этой вспомогательной поверхности относительно данных поверхностей должны быть выбраны так, чтобы в пересечении получились простые по форме линии (прямая, окружность) и чтобы проекции этих линий легко строились на комплексном чертеже.

В качестве вспомогательных поверхностей чаще всего используют либо плоскости, либо сферы.

Построение линии пересечения поверхностей следует начинать с определения её опорных точек. К ним относятся:

1)экстремальные – наивысшая и наинизшая, крайняя левая и крайняя правая, самая ближняя и самая дальняя;

2) точки видимости, разделяющие видимую часть кривой от невидимой, и имеющие свои проекции на линиях очертания поверхностей.

Опорные точки почти всегда позволяют видеть, в каких пределах нужно изменять положение вспомогательных секущих поверхностей для нахождения остальных, так называемых произвольных или промежуточных, точек.

Примеры пересечения поверхностей

Пример 1. Построить линию пересечения кругового конуса со сферой (рисунок 1.3.53).

Рисунок 1.3.53 – Пересечение конической и сферической поверхностей

Задача решается способом секущих плоскостей-посредников. Следует отметить, что у обеих поверхностей имеется общая плоскость симметрии, которая проходит через ось симметрии конуса и центр симметрии сферы. Эта плоскость обозначена Ф(Ф₁). Она определяет опорные точки 1(1₂) – высшую и 2(2₂) – низшую. Горизонтальные проекции этих точек 1₁ и 2₁ расположены соответственно на линии Ф₁. К опорным следует отнести и точки А, В, определяющие видимость линии пересечения данных поверхностей на горизонтальной плоскости проекций П₁. Эти точки находятся в плоскости экватора Γ(Γ₂) сферической поверхности, которая пересекает конус по окружности радиуса R, а сферу по экватору. В пересечении горизонтальных проекций этих линий получаем точки А₁ и В₁. Фронтальные проекции А₂ и В₂ точек видимости А и В определяются соответственно на линии Γ₂.

Далее определяем нужное количество промежуточных (произвольных, случайных) точек, используя для этого вспомогательные горизонтальные плоскости-посредники, одна из которых Γ¢(Γ¢₂) показана на чертеже. С её помощью построены точки 3 и 4. Плоскость Γ¢(Γ¢₂) пересекает конус и сферу по соответствующим окружностям, которые проецируются в натуральную величину на плоскость П₁. Их пересечение позволяет определить первоначально горизонтальные проекции 3₁, 4₁ точек 3 и 4, а затем по линии связи фронтальные проекции этих точек соответственно на линии Γ¢₂.

Построенные точки соединяют на обеих проекциях с учётом видимости плавной кривой с помощью лекала.

На фронтальной проекции половина кривой находится на задней стороне данных поверхностей. Но невидимая её часть закрывается видимой. На горизонтальной проекции видна часть кривой, на которой находятся точки 1, А, В, расположенные выше экватора сферы. Очерковая образующая фронтальной проекции конуса между точками 1 и 2 находится внутри сферы и изображена поэтому сплошной тонкой линией. Точно так же изображена часть линии очерка сферы, находящаяся внутри конуса. На горизонтальной проекции тонкой линией показана часть окружности экватора, находящаяся внутри конуса.

Пример 2. Построить линию пересечения двух конических поверхностей вращения (рисунок 1.3.56).

В данном случае в качестве вспомогательных поверхностей используются концентрические сферы. Но прежде чем рассмотреть решение этой задачи, остановимся на одном частном случае пересечения поверхностей вращения.

Пусть две такие поверхности имеют общую ось, т.е. являются соосными. В этом случае они будут пересекаться по окружностям, число которых равно числу точек пересечения меридианов поверхностей.

Пусть одна поверхность образуется вращением меридиана m(m₂), а другая – вращением меридиана n(n₂) около общей оси i(i₂) (рисунок 1.3.54). При этом общие точки А(А₂), В(В₂), С(С₂) меридианов образуют окружности, общие для данных поверхностей, и число таких окружностей равно числу точек пересечения меридианов.

Рисунок 1.3.54 – Образование соосных поверхностей вращения

Рисунок 1.3.55 – Пересечение соосных поверхностей вращения

Предположим, что некоторая поверхность вращения пересекается со сферой, причём центр сферы находится на оси этой поверхности. При таком условии сфера будет соосной с поверхностью, и в пересечении получается окружность (рисунок 1.3.55).

Свойство сферы, имеющей центр на оси поверхности вращения, пересекать поверхность по окружностям является основой способа концентрических сфер.

Способ концентрических сфер применяется при следующих условиях:

1) пересекающиеся поверхности являются поверхностями вращения;

2) оси поверхностей пересекаются;

3) пересекающиеся оси образуют общую плоскость симметрии, параллельную плоскости проекций.

В рассматриваемом примере (рисунок 1.3.56) оси вращения данных конусов i, l пересекаются в точке О(О₁, О₂) и образуют общую плоскость симметрии Ф(Ф₁), параллельную фронтальной плоскости проекций П₂.

Вначале определяем опорные точки. Это наивысшая точка 1 и наинизшая точка 2, которые расположены в общей плоскости симметрии Ф(Ф₁) и получаются в пересечении главных меридианов данных конусов. Исходя из этого отмечаем фронтальные проекции 1₂ и 2₂ точек 1 и 2. Горизонтальные проекции 1₁ и 2₁ этих точек отмечаем на линии l₁ ≡ Ф₁. К опорным отнесём и точки, полученные при помощи вспомогательной секущей сферы наименьшего радиуса, проведённой из точки О₂. Для определения этого радиуса нужно из точки О₂ провести две нормали к очерковым линиям поверхностей и выбрать большую из них. Если в качестве радиуса вспомогательной сферы взять меньшую нормаль, то одна из данных поверхностей с такой сферой не пересечётся. В данном примере с помощью сферы наименьшего радиуса построены точки А и А^¢. Эта сфера (на чертеже она изображается окружностью) касается конуса с осью вращения i, а конус с осью вращения l пересекает. И касание, и пересечение осуществляются по окружностям, которые на фронтальной проекции изображаются отрезками. В их пересечении получаются точки А₂ ≡ А^¢₂.

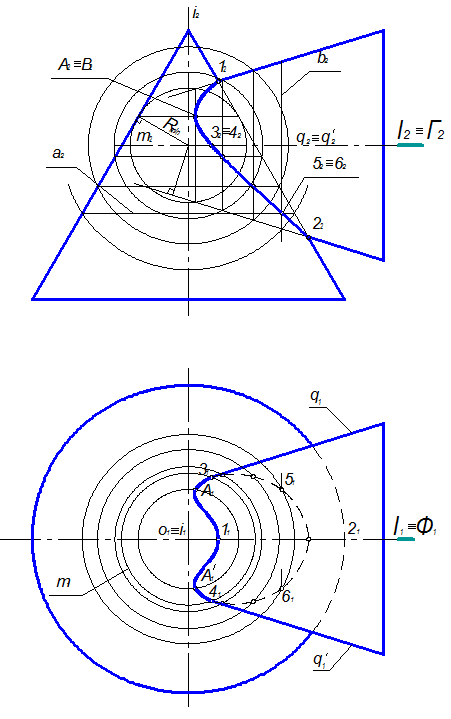
Рисунок 1.3.56 – Способ концентрических сфер

Горизонтальные проекции А₁, А^'₁ точек А и А^' построены при помощи окружности-параллели конуса с осью i, по которой вспомогательная сфера наименьшего радиуса касается этого конуса. Точки 3 и 4 видимости линии пересечения данных поверхностей на плоскости П₁ также относятся к опорным точкам. Они определяются при помощи плоскости Γ(Γ₂), проведённой через ось вращения l второго конуса. Эта плоскость пересекает конус с осью i по окружности m(m₂, m₁), а второй конус – по образующим q и q₁, которые совпадают с его осью. Горизонтальные проекции 3₁, 4₁ точек видимости 3 и 4 получаются в пересечении окружности m₁ с линиями q₁ и q^'₁.

Фронтальные проекции 3₂ ≡ 4₂ этих точек определяются на линии l₂ ≡ Γ₂. На плоскости П₁ видимыми являются точки, расположенные на линии пересечения выше плоскости Γ(Γ₂). Это точки 1, А, А^', 3 и 4. Промежуточные точки линии пересечения определены с помощью сфер, проведённых из центра О₂, радиусы которых больше радиуса R_min – радиуса наименьшей сферы, но меньше радиуса наибольшей сферы, которая может быть проведена через наиболее удалённую точку 2₂ линии пересечения.

Ввиду того, что точка 2 определяется с помощью общей плоскости симметрии Ф(Ф₁), нет необходимости использовать сферу наибольшего радиуса. Определение промежуточных точек линии пересечения можно видеть на примере построения точек 5 и 6. Фронтальные проекции 5₂, 6₂ этих точек получены в пересечении линий a₂ и b₂, которыми изображаются фронтальные проекции соответствующих окружностей a и b как принадлежащих одной и той же вспомогательной сфере-посреднику, соосной с данными поверхностями. Горизонтальные проекции 5₁, 6₁ точек 5 и 6 построены при помощи окружности-параллели а конуса с осью i.

Вспомогательные сферы-посредники могут быть и эксцентрическими, т.е. имеющими различные центры. Они применяются при следующих условиях:

1) из двух пересекающихся поверхностей одна является поверхностью вращения, а другая имеет семейство круговых сечений;

2) оси поверхностей в общем случае не пересекаются;

3) поверхности имеют общую плоскость симметрии, параллельную плоскости проекций.