Матрыца лінейнага адлюстравання.

Няхай V,W-л.п. над Р.

v₁,v₂,…,v_n (1) –базiс V.

w₁,w₂,…,w_k (2)– базiс W.

Адлюстраванне fÎ L(V,W) адназначна вызначаецца вектарамi:

f (v₁), f (v₂),…, f (v_n) (3)

З таго, што (2)– базiс W => кожны вектар

_k

f(v_i)=∑ a_jiw_j , a_jiÎР (4)

^j=1

Матрыца А=( a_ji)ÎР_kxn наз. матрыцай лін.адл. f у баз.(1) і (2).

Часцей за усё будзем разглядаць выпадак, калі V=W (1)=(2), тады A-матрыца f у базiсе (1).

Прыклады:

1) V,W адвольныя лін.пр-ры над полем Р Ө: V® W

(1),(2) – адвольныя базісы V і W адпаведна.

Тады матрыца Ө у базісах (1)і (2) відавочна нулявая матрыца О_kxn

2) Матрыца тоеснага адл.e: V® V -- матрыца е у базісе(1) -- E_n

А (па слупках каардынаты f (v_i) у базісе (2))

Тэарэма 1:Няхай f ÎL(V,W). А-матрыца f у базiсах (1),(2); аÎV з каард.слупком X у базiсе(1),тады f (а) мае каар-ны слупок А X у базiсе (2).

Доказ: В=(v₁,v₂,…,v_n), C=(w₁,w₂,…,w_k) 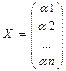a_jiÎР

аÎ V, а=ВX

ВX= α₁v ₁+ α₂v ₂+…+α _nv_n

f (а)=f(α₁v ₁+ α₂v ₂+…+α _nv_n)= α₁ f (v ₁)+ α₂ f (v ₂)+...+ α f_n (v _n)=( f (v ₁)* f (v ₂)*....* f_n (v _n))Х

З азн. матрыцы лiн. адлюстравання вынікае, што ( f (v ₁)* f (v ₂)*....* f_n (v _n))=СА.

f (а)=(СА)X=С(АХ) =>АХ-каар-ны слупок f (а) у базiсе (2).

Тэарэма 2:Няхай А ÎР_kxn, f:V®W такое , што адвольнаму вектару аÎV з каар-ным слупком X у базiсе (1) ставіць у адпаведнасць f (а)ÎW з каар-ным слупком АХ у базiсе (2), тады адлюстраванне f -лiнейнае і матрыца f у базiсах (1),(2) роуная А.

Доказ:1)" a,bÎ V трэба паказаць, што f (a+b)= f (a)+ f (b). Няхай Х,У-каардынатныя слупкі a,b у базісе (1) адпаведна. Тады Х+У – каардынатны слупок (а+ b) у б.(1).

Таму f(a+b) Î W з каард.слупком А(Х+У) у б.(2)

А(Х+У)=АХ+АУ, АХ-каард.слупок f (a) у б.(2), АУ-каард. w (f(а)) у б.(2).

АХ+АУ – каард.слупок f (a)+ f (b) => f (a+b)= f (a)+ f (b).

Аналагічна даказваецца f(aa)= a f (a), aÎР.

0 0

0 0

... ...

0 0

1 - і-ты радок f(v_i), А 1 у базісе (2)

0 0

... ...

0 0

Няхай А – матрыца з каэфіцыэнтамі А= a_ij ÎР_k×n

0 α_1і

... α_2і

0 ...

А= 1 - і= α_кі => матрыца f у базісах (1),(2) – (α_jі)=A

...

Hяхай U-л.п. над Р

u₁,u₂,…,u_n (5) базiс л.п. U.

Тэарэма 3:Няхай f, g лін.адл. f, g ÎL(V,W), hÎL(V, U).А і В-матрыцы f і g адпаведна у базiсах (1) (2). С – матрыца h у базісах (2),(5). a - адвольны скаляр з поля Р. Тады А+В i aA ёсць матрыцы лін.адл. f + g i a f адпаведна у базiсах (1),(2), а СА- матрыца лін.адл. hf у базiсах (1),(5).

Доказ: f + g – лін.адл. ÎL(V,W)

аÎV, X- каар-ны слупок у базiсе (1) мае а. Тады (f + g)(a)==азн.адл.== f (a)+ g (a).

f (a) мае у базiсе (2) - каар-ны слупок АХ;

g (a) мае у базiсе (2) - каар-ны слупок ВХ;

Тады

f (a)+ g (a) мае каар-ны слупок АХ+ВХ у б.(2)

АХ+ВХ=(А+В)Х

(f + g)(a) мае каар-ны слупок (А+В)Х у б.(2)

(А+В) – ёсць матрыца (f + g) у б.(2)

hfÎL(V, U)

"аÎV, Х- каард.слупок а у б.(1)

(hf)(а)= h(f(а))

f (a) мае у базiсе (2) - каар-ны слупок АХ;

h(f(а)) мае у базiсе (5) - каар-ны слупок С(АХ)=(СА)Х

h(f(а)) мае у базiсе (5) - каар-ны слупок СА(Х)

СА – ёсць матрыца лін.адл. hf у б. (1),(3).

Кожнаму лін.адл. f ÎL(V,W) паставілі у адпаведнасць матрыцу АÎР_k×n – матрыца f у б.(1),(2)

Гэта адл. ёсць біекцыя f ®А, g® А

f (v_i) = g(v_i), і=1,n => f = g зн. наша адл. - ін`екцыя.

"АÎР_k×n існуе fÎL(V,W), А – матрыца f у б. (1),(2) (Т2)

Суме лін.адл. адпавядае сума матр.здаб. лін.адл. на a адпав. здабытак матрыцы гэтага адл.на a.

Пры n=k здаб. N адл. Адпав. здабытак матрыцау

14 Ізамарфізм лінейных прастораў.Азн. уласц. Прыклады.Крытэр ізаморфнасці лін.пр.

Азн:Няхай V, W – л.п над P. Біекцыйнае л.а ƒ: V → W наз ізамарфізмам л.п. (незвыродным л.а) пр-ры V на пр-ру W. Калі існуе які-небудзь ізамарфізм пр-ры V на W будзем казаць што V ізаморфна W і пісаць V@W. Із-зм пр-ры V на сябе наз. аутамарфізмам лін.пр-ры V.

Прыклад:Няхай V – п-мерная л.п. над Р d_­1,d₂,....d_п – (1) нек базіс V

Адлюстраванне j: V-Р^п_, аÎ V ставіць у адпаведнасць каард. слупок Х у базісе(1) ёсць із-зм лінейных пр-рау. j(а)= j(b) => а= b .зн. j-інекцыяі сюрекцыя =>j-біекцыя.

Уластівасці ізамарфізмаў л.п.

1)для адв. лін. пр-ры V е: V→ V – аутамарфізм або V@V ( V ізаморфна сама сабе).

2)калі j:V→W із-зм, тады j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­^-1: W→V-із-зм,

Доказ: Пакажам, што j ­­­­­­­­­­­­­­­­­­­­­­­­­­­­­^-1 – лінейн. адл. "а,в_­ÎW "a,bÎР j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ ^-1(aа+bв) з таго што j-биекцыя выникае што а=j(а₁) в=j(в₁), а₁, в₁ÎV, тады j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ ^-1(aа+bв )= j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­^-1(aj(а₁)+bj­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ (в₁))= j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ ^-1(j(aа₁+bв₁))= ­­­­­­­­­­­­­­­­­­­­­­­­­ =aа₁+bв₁= ­­­­­­­­­­­­­­­­­­­­­­­­­­ ­­­­­­­­­­­­­­­­­­aj­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ ^-1(а)+b j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ ^-1 (в )

3) Няхай j:V→W g: W → U- лин.адл. => gj:V→ U- лин.адл.

Доказ: "а,в_­ÎV "a,bÎР (gj)(aа+bв )= g(j­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ (aа+bв))= g (aj(а)+bj­­­­­­­­­­­­­­­­­­­­­­­­­­­­­ (в))= ag(j(а))+ b g (j(в))=

=a(gj)(а)+b(gj)(в)

4)Няхай j:V→W – із-зм тады

Калі а₁, а₂,… а_к -лін.незал. сіс-ма вектарау з пр-ры V ,тады j(а₁), j(а₂), …j(а_к) –лін. незал. Сіс-ма вектарау з W.

Доказ:Возьмем адв. лін.камб. a₁j(а₁)+ a₂j(а₂)+…+a_кj(а_к)= Ō’ j(a₁а₁+a₂а₂+…+a_ка_к )= Ō’

j( Ō)= Ō’=>a₁а₁+a₂а₂+…+a_ка_к = Ō=>a₁ =a₂ =…=a_к =0.

5) Калі а₁, а₂,… а_п – базіс лін. пр-ры V тады j(а₁), j(а₂), …j(а_п) –базіс W. У прыватнасці памернасць пр-ры dim V =dimW.

Тэарэма Няхай v₁, …,v_п – (1)базіс V jєL(V,W)- лін. адл. . j зяул. із-мам лін. пр-рау калі і т. к.

j( v ₁), j(v ₂), …j (v _п)-(2) базіс пр-ры W.

Доказ:Неабх. з уласц. 5.

(Даст.) jєL(V,W)(2) базіс пр-ры W . Трэба даказаць што j біекцыя

"а,в_­ÎV няхай j(а)= j(в) а=a₁v₁+…+a_пv_п в=b₁ v₁+…+b_п v_п a_і,b _і ÎР і=1,п

j(a₁v₁+…+a_пv_п)= j(b₁ v₁+…+b_п v_п) =>a₁j(v ₁)+ …+a_пj(v _п )= b₁j(v ₁)+…+ b_пj(v_п) =>a _і=b _і і=1,п

Зн. а=в j- інекцыя

"wєW=>w=a₁j(v ₁)+ …+a_пj(v _п )= j(a₁v₁+…+a_пv_п) зн. j - сюрекцыя=>j біекцыя.

Вынік1(Крытэр із-сці) 2 канцамерныя лін. пр-ры над полем Р ізаморфныя калі і т. к. іх памернасці роуныя.

Доказ: Неабх. – уласц.4.

(Даст.) Няхай dim V =dimW=п (1)-базіс V w₁, ….w_п – (3) базіс пр-ры W. Па т-ме існуе лін. адл. jєL(V,W)j(v _і)= w_і і=1,п => j-із-зм . V@ Р^п W@Р^п => V@W

Вынік1’ Для фікс. Натуральнага піснуе адзіная( з дакладнасцю да із- зму) лін. пр-ра памернасці пнад полем Р - Р^п .