Молекулярно-кинетическая теория газов.

Основные положения молекулярно-кинетической теории, которые ообъяснили открытые к тому времени газовые законы, были высказаны в середине XVIII в. русскими учёными М.В. Ломоносовым и Д. Бернули. В кинетической теории идеального газа имеются некоторые допущения:

1. Молекулы рассматриваются как математические точки. В общем случае под точкой понимают некий объект, в самом общем случае вообще лишённый протяжённости в пространстве. В геометрическом смысле под точкой понимают некоторую прямую, начало и конец которой совпадают. В самом же простейшем случае под точкой можно понимать прямую, которой наблюдатель смотрит в торец.

2. Силы взаимного притяжения между молекулами настолько малы, что ими можно в общем случае пренебречь.

3. Молекулы находятся в непрерывном хаотическом движении. Даже при сверхнизких температурах, вблизи абсолютного нуля , когда хаос тепловых колебаний затухает, молекулы всё равно колеблются за счёт энергии так называемых нулевых колебаний. Так, имеем соответственно:

где

или

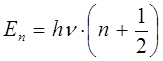
где

Спектр квантового осциллятора, описываемый уравнениями такого типа, называется эквидистантным или равноотстоящим. Как можно заметить, энергия здесь начинается с ненулевого значения:

или

тогда как в классической механике в состоянии покоя:

и как следствие:

Таким образом, квантовый осциллятор, в отличие от своего классического аналога, никогда не находится в состоянии покоя. Даже в состоянии с наименьшей энергией частица колеблется (что находится в полном соответствии с принципом неопределённости Гейзенберга):

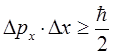
если бы такого не происходило (отсутствовала энергия нулевых колебаний ), тогда в силу вступали бы законы классической механики, т.е. существовала бы возможность одновременного измерения двух физических величин – координаты и импульса частицы. Существование ненулевого значения энергии находит своё отражение в физических явлениях, возникающих при низких температурах (в том числе и при ). Так, рассеяние света кристаллами обусловлено колебаниями атомов кристаллической решётки. При понижении температуры, амплитуда колебаний понижается, однако сами колебания как показали экспериментальные данные, не прекращаются и вблизи абсолютного нуля. Это в свою очередь приводит к соответствующему рассеянию света. Другой важный пример – нулевые колебания вакуума. Так, электромагнитное поле описывается набором осцилляторов, представляющих колебания векторов напряжённости электрического и магнитного поля. Квантование осцилляторов поля позволяет правильно интерпретировать основное его состояние – вакуум. Так, в вакууме , но из-за нулевых колебаний электромагнитное поле флуктуирует, т.е. 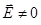. Это, в свою очередь, приводит к флуктуациям координаты электрона в атомах и молекулах, а, следовательно, к смещению всех энергетических уровней (так называемый лэмбовский сдвиг). Хотя сам сдвиг и незначителен (например, в атоме кислорода эВ), он имеет принципиальное значение, подтверждая, таким образом, существование наличия нулевых колебаний и таким образом основные концепции квантовой механики. Именно в области низких и сверхнизких температур происходит фазовый переход 2-го рода и проявляется квантовая природа вещества в макроскопическом масштабе в виде таких интересных явлений как, например, сверхпроводимость и сверхтекучесть, эффект Мейснера, изотопический эффект др.

4. При столкновении молекул, общее количество их кинетической энергии не изменяется. При столкновении молекул происходит изменение направления и скорости их движения, но общее количество, запас кинетической энергии будет неизменным. Поэтому в любой данный момент времени имеются молекулы, движущиеся с различными скоростями. Однако благодаря огромному количеству молекул, равному числу Авогадро:

скорость их движения всегда можно выразить некоторой средней (усреднённой) величиной. Для данной температуры средняя скорость молекул есть величина постоянная, не меняющаяся во времени. При расчётах нередко пользуются средней квадратичной скорости:

Это связано, прежде всего, с тем, что квадраты скоростей независимо от направления скорости движения молекул имеют один и тот же знак. Кинетическая теория газов даёт возможность связать давление и объём со средней квадратичной скоростью движения молекул . Как известно, каждая частица может двигаться в трёх неэквивалентных направлениях – , 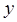и 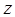. Поскольку согласно молекулярно-кинетической теории газов молекулы находятся в непрерывном, хаотическом движении, то это в свою очередь означает, что не одно из направлений их движения не является преимущественным. Для вывода основного уравнения кинетической теории газов, выделим в пространстве небольшой участок пространства в виде куба объёмом равным , содержащим молекул, движущихся в выделенном объёме со среднеквадратичной скоростью и обозначим массу молекул идеального газа через :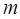

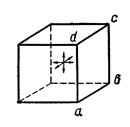
Рис.8. Схема для вывода основного уравнения кинетической теории газов.

Известно, что давление газа на стенку сосуда измеряется тем количеством движения, которое получает эта стенка за от ударов молекул на её поверхности. Очевидно, что давление газа на стенку сосуда будет тем больше, чем чаще и с большей силой будут ударять эти молекулы в эту самую стенку, что хорошо видно из детального анализа выражения 2-го закона Ньютона.

Для более глубокого понимания данного вопроса, рассмотрим движение частицы с массой m, представляемой в виде движущейся материальной точки. Под материальной точкой, в общем случае, понимают тело (частицу), обладающее массой, размерами и формой которого в условиях данной задачи можно пренебречь. В декартовой системе координат, положение частицы в данный момент времени задаётся радиус-вектором:

указывающим положение материальной точки в пространстве. При этом векторы в трёхмерном пространстве задаются не только тройкой компонент x, y и z, но и явным разложением по ортам координатных осей :

Для движущейся точки каждая из проекций , а, следовательно, и радиус-вектор являются функциями времени 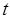. В общем случае, движение материальной точки определяется тремя скалярными уравнениями вида:

которые представляют собой не что иное, как параметрическое задание некоторой кривой и таким образом уравнение вида:

будет определять траекторию движения частицы (материальной точки). Тогда основное уравнение динамики механической системы:

с учётом приведенных выше соображений:

а также учитывая, что:

будем иметь соответственно выражение вида:

Из курса классической механики также хорошо известно, что:

тогда из выражения вида:

следует, что:

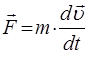
и соответственно:

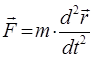
Из курса классической механики также хорошо известно, что:

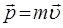
или с учётом того, что:

имеем:

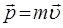
откуда:

Итак, в ходе поделанных нами выше выкладок, мы пришли к двум важным для наших дальнейших рассуждений выражениям:

а также:

тогда, с учётом приведенных выше соображений, будем иметь соответственно:

откуда следует, что:

или с учётом того, что:

будем иметь соответственно:

Действительно, после соответствующих подстановок, полученное нами выше аналитическое выражение 2-го закона Ньютона:

может быть представлено к виду:

Полученное выше основное уравнение динамики механической системы:

с учётом выражения:

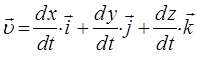
может быть представлено далее к виду:

и таким образом будем иметь соответственно:

Очевидно общее решение:

в виде явной функции

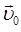включает произвольные постоянные, значение которых определяют из начальных условий. Например, в заданный момент времени привязываем конкретные величины и радиус-вектору , и соответственно вектору скорости , для которого, как и для случая радиус-вектора :

где

Подобный выбор начальных условий (начальное положение и скорость) в виде:

является наиболее целесообразным, однако возможны и другие способы выделения частного решения из общего. Важно, что по теореме Коши частное решение всегда существует и является единственным. Тем самым эволюция механической системы, её развитие во времени всегда строго детерминирована. Это и есть лапласовский детерминизм классической механики. Возвратимся теперь от классической механики к молекулярно-кинетической теории газов, выводу основного уравнения. Так, на основании проделанных нами выше выкладок, мы пришли к основному уравнению динамики механической системы:

Это в свою очередь означает, что количество движения (импульс) при ударе частицы о стенку сосуда, будет полностью определять силу удара, что хорошо видно из аналитического выражения 2-го закона Ньютона. Так, действительно при ударе молекулы о стенку сосуда, она сообщает ей количество движения (импульс):

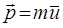
где – импульс частицы; – средняя квадратичная скорость молекулы. Сообщив стенке сосуда импульс равный , молекула при упругом отражении получает импульс равный сообщённому стенке сосуда, но только уже с обратным знаком, т.е.

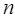Обозначим давление газа на стенку сосуда – , а число ударов – . Тогда если число ударов молекул о стенку сосуда за будет равно 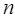, то очевидно на стенку сосуда будет оказываться давление , равное:

Поскольку, как было сказано уже выше, движение молекул беспорядочно и не одно из направлений в пространстве не является преимущественным, то очевидно к каждой из шести граней куба будет двигаться молекул. Так как скорость молекул газа, заключённых в сосуд объёмом будет равна , то очевидно число ударов 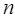, приходящихся на стенки сосуда будет равно:

Учитывая, что:

после подстановки будем иметь соответственно:

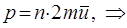
Пусть у нас имеется 1 моль газа, тогда:

или после подстановки в уравнение:

будем иметь соответственно:

Полученное нами выше уравнение:

является основным уравнением молекулярно-кинетической теории. Учитывая, что:

будем иметь соответственно:

Рассмотрим теперь более подробнее основное уравнение молекулярно-кинетической теории газов, полученное нами уже выше:

Так, например, умножив и разделив одновременно член на два, будем иметь соответственно:

Принимая выражение:

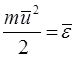
где – средняя кинетическая энергия молекулы газа, после подстановки в основное уравнение молекулярно-кинетической теории будем иметь:

и соответственно:

откуда будем иметь:

или принимая:

где 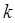– постоянная (константа) Больцмана. Тогда будем иметь соответственно:

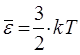
Поскольку:

принимая:

где – кинетическая энергия 1 моль газа. Тогда будем иметь соответственно:

и таким образом, имеем соответственно:

Из уравнения:

можно легко найти далее среднюю скорость движения молекул. Так, имеем:

откуда:

и далее:

откуда получаем:

или в окончательном виде:

здесь:

и соответственно: