
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Скорости движения молекул идеального газа.
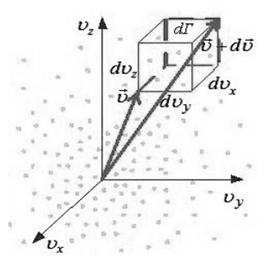
Рис.10. Распределение молекул по скоростям.
Давление идеального газа на стенки сосуда определяется средней силой взаимодействия молекул со стенкой сосуда. Согласно второму закону Ньютона сила, с которой стенка сосуда действует на молекулу:
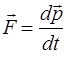
Вектор импульса 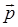 зависит от скорости молекулы, поэтому очень важно знать, каковы скорости молекул. Эту задачу решил в 1859 г. Дж. Максвелл. При этом он исходил из следующих основных положений: газ состоит из большого числа одинаковых молекул; молекулы газа находятся в непрерывном хаотическом движении; газ находится в равновесном состоянии. Температура, давление и другие параметры идеального газа постоянны; на газ действуют внешние силовые поля. Максвелл получил функцию распределения, справедливую для равновесного состояния, в котором устанавливается стационарное (не зависящее от времени) распределение молекул по скоростям. Функция распределения
зависит от скорости молекулы, поэтому очень важно знать, каковы скорости молекул. Эту задачу решил в 1859 г. Дж. Максвелл. При этом он исходил из следующих основных положений: газ состоит из большого числа одинаковых молекул; молекулы газа находятся в непрерывном хаотическом движении; газ находится в равновесном состоянии. Температура, давление и другие параметры идеального газа постоянны; на газ действуют внешние силовые поля. Максвелл получил функцию распределения, справедливую для равновесного состояния, в котором устанавливается стационарное (не зависящее от времени) распределение молекул по скоростям. Функция распределения 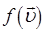 , позволяет найти вероятность того, что составляющие скорости вдоль декартовых осей координат лежат в интервалах:
, позволяет найти вероятность того, что составляющие скорости вдоль декартовых осей координат лежат в интервалах:
от 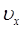 до
до 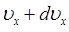
от  до
до 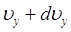
от 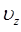 до
до 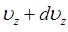
Тогда вероятность найти молекулу в указанном выше интервале скоростей, очевидно, будет определяться на основании выражений вида:



Функция распределения молекул идеального газа
По компонентам скорости.
Молекулы движутся хаотично, внешних воздействий на них нет, следовательно, вероятности того, что молекула движется вдоль оси 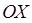 ,
,  или
или 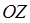 одинаковы. Функция распределения определяет вероятность, поэтому функции распределения молекул по проекциям скорости на оси координат:
одинаковы. Функция распределения определяет вероятность, поэтому функции распределения молекул по проекциям скорости на оси координат:
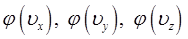
должны иметь одинаковый вид. Факт движения молекулы вдоль направления одной из осей координат не зависит от того, движется ли эта молекула вдоль другой оси, поэтому эти события (движение вдоль одной из осей координат) независимы. Согласно теории вероятностей, вероятность того, что произойдут несколько независимых событий, равна произведению вероятностей каждого из событий в отдельности:
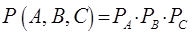
Поэтому и функцию распределения, которая определяет вероятность того, что молекула имеет вектор скорости, компоненты которого равны:
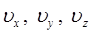
можно представить, как:

Вычислим натуральный логарифм от этого выражения:
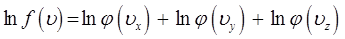
и далее полученное выражение, продифференцируем по 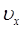 :
:
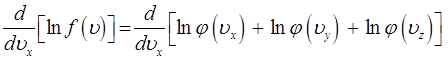
Учитывая, что:

поэтому в левой части после дифференцирования получим:

в правой части будем иметь соответственно:
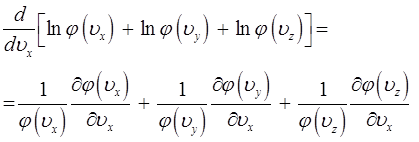
Однако, учитывая, что:
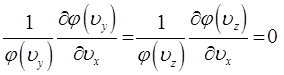
будем иметь соответственно:
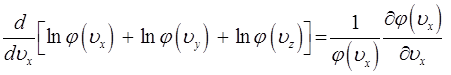
Возвращаясь к исходному выражению:
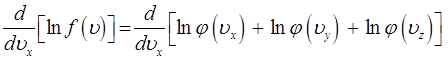
имеем соответственно:

а также:
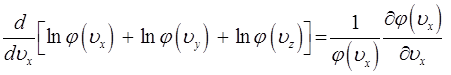
Приравнивая между собой результаты дифференцирования правой и левой частей исходного выражения:
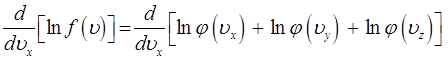
получим уравнение вида:
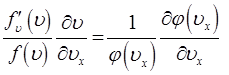
откуда соответственно:

В полученном нами выше выражении вычислим производную:
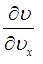
разлагая квадрат скорости 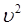 по трём компонентам
по трём компонентам  ,
, 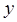 и
и 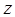 :
:

тогда будем иметь соответственно:

полученный нами выше результат дифференцирования подставим в уравнение:

откуда:
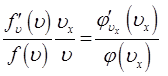
или после разделения переменных:
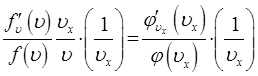
откуда соответственно:
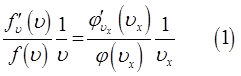
Аналогично можно получить уравнения для функций распределения по другим составляющим скорости:
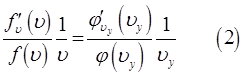
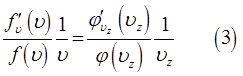
Итак, имеем соответственно:
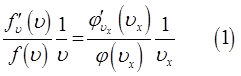
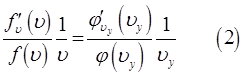
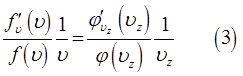
Из полученных нами выше уравнений (1), (2) и (3) хорошо видно, что левая часть данных выражений одинакова, а значит, последняя, не будет зависеть и от составляющих скорости. Поскольку левая часть полученных нами выше уравнений, не зависит ни от каких переменных, то левую часть каждого из уравнений, в общем случае, можно будет принять за константу, т.е.

тогда уравнения для функций распределения можно будет переписать в виде:

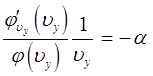
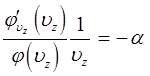
Для того чтобы определить функцию:
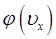
рассмотрим первое из полученных нами выше уравнений:

откуда:
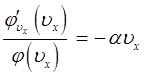
и проинтегрируем данное уравнение по компоненте скорости 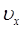 :
:
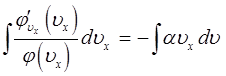
откуда:
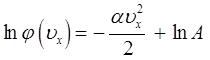
здесь произвольную постоянную мы выбрали в виде:

и таким образом, в ходе проделанных выкладок, приходим к уравнению вида:
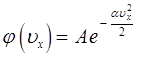
или
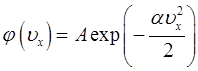
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...