Формула полной вероятности и формула Байеса

Если событие А может произойти только при выполнении одного из событий , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле

.

Эта формула называется формулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий , вероятности появления которых . Событие А может произойти только вместе с каким-либо из событий , которые будем называть гипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез .

По теореме умножения вероятностей

,

откуда

.

Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез называются апостериорными вероятностями, тогда как - априорными вероятностями.

Пример. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.

Можно применить формулу полной вероятности, причем в наших обозначениях:

Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:

Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

- на линию огня вызван первый стрелок,

- на линию огня вызван второй стрелок,

- на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то

В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

по формуле Байеса находим вероятность гипотезы после опыта:

Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: – взятая наудачу деталь обработана на -ом станке, .

Условные вероятности (в условии задачи они даны в форме процентов):

Зависимости между производительностями станков означают следующее:

.

А так как гипотезы образуют полную группу, то .

Решив полученную систему уравнений, найдем: .

а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:

.

Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%.

б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:

,

,

.

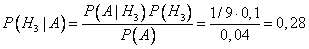Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.

8.

Рассматриваются теорема Муавра-лапласса и формулы Бернулли и Пуассона.

Рассмотрим пример. Пусть Некто бросил монетку два раза. Считая каждый исход "орел" - "решка" равновероятным и независимым от предыдущего результата, получим следующие варианты результатов:

.

где обозначено появление - "решки" и 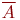- "орла". Понятно, что при этом , так как появление "орла" или "решки" события равновероятные. Для удобства введем обозначение 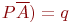. Очевидно, что .

Пусть теперь монету кидают 3 раза. Теперь возможны разных вариантов исходов:

Можно убедиться самостоятельно, что, если монетку кидать 4 раза, то получится различных вероятных комбинаций.

Рассуждая далее, имеем, что в случае испытаний Некто получит одну из комбинаций исходов.

Так как испытания независимые, то, применяя теорему умножения вероятностей найдем вероятности каждого из проведенных испытаний (табл. 5.1 для ; табл. 5.2 для ).

Таблица 5.1. Вероятности четырех исходов, двух независимых испытаний

Исход

Вероятность

Таблица 5.2. Вероятности восьми исходов трех независимых испытаний

Исход

Вероятность

Исход

Вероятность

Исход

Вероятность

Исход

Вероятность

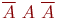
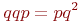
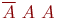
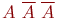
Проанализируем табл. 5.2 более подробно. Заметим, что не появление события А во всех трех испытаниях имеет вероятность , соответствующую только одному единственному исходу . Тогда вероятность, появления события А один раз соответствует (см. табл. 3)

Аналогично, вероятность появления 2-х раз А будет равна .

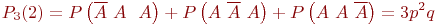
И, наконец, если событие А состоялось все три раза, то

Можно убедиться, что эти события образуют полную группу, т.е.

Если рассмотреть вероятность , вероятность появления собы-тия А m раз в n испытаниях, то, рассуждая так, как это было представлено ранее получим формулу

(1)

которая известна как формула Бернулли.Эта формула определяет вероятность появления события А раз в испытаниях. В формулу входит коэффициент , который читается как число сочетаний из исходов по раз. Более коротко число сочетаний из по . Вычисляется по простой формуле:

Пример 1. В ящике лежат 20 белых и 10 черных шара. 4 раза извлекали шар, причем после каждого раза взятый шар возвращался в ящик и все шары тщательно перемешивались. Найти вероятность того, что 2 раза из 4-х был извлечен белый шар.

Решение. Решим задачу двумя способами.

1 способ. Обозначим событие – "вытащили белый шар", - "вытащили черный шар". Тогда рассмотрим все возможные комбинации появления шаров. Таких комбинаций будет :

Нас интересуют только те исходы, в которых появляются по 2 раза белые и черные шары. Всего таких исходов 6. Вероятность вытащить белый шар в каждом из испытаний, так как по условию задачи шарик после испытания возвращается в ящик. Аналогично вычисляем вероятность извлечения черного шарика . Подсчитаем теперь искомую вероят-ность: ,

где 6 - количество благоприятных исходов; - вероят-ность появления белого шара в любых 2-х испытаниях; - вероятность появления черного шара в любых 2-х испытаниях.

2 способ. Для решения воспользуемся формулой Бернулли (1):

Как видим ответы совпадают, однако первый способ не всегда удобен в применении. Особенно, если речь идет о значительном количестве испытаний.

Пример 2. Вероятность попадания стрелка в цель 0,8. Стрелок делает 10 выстрелов. Найти вероятность, что цель будет поражена 8 раз.

Решение. Для решения задачи воспользуемся формулой Бернулли:

Можно легко убедиться в справедливости следующих равенств:

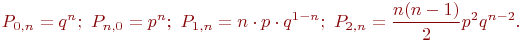
Все эти формулы являются частным случаем формулы (1).

При испытаниях некоторое событие, имеющее вероятность может появиться несколько раз, однако, если обозначить - наименьшее количество раз появление некоторого события при испытаниях, то получим

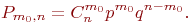
(2)

Очевидно, что выполняется при , т.е. - это гарантированное число появлений события при испытаниях. Иными словами, появление события большее количество раз или меньшее будет менее вероятным, чем . Если и , тогда можно записать

(3)

где - наивероятнейшее число появления события А при испытаниях; - вероятность появления события А при одном испытании; .

Если и не целые числа, то тогда они округляются до ближайшего целого, но так, чтобы интервал не увеличивался.

Пример 3. В ящике лежат 100 отшлифованных поделочных камня и 80 не шлифован-ных. Из ящика извлекают 20 камней. Какое наивероятнейшее число шлифованных камней будет извлечено при этом.

Решение. Определим и - вероятности извлечения и шлифованного, и не шлифованного поделочного камня. Так как общее число камней в ящике 180, то эти вероятности просто подсчитать:

Тогда определим по формуле (3):

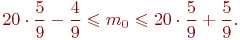
Округлим левую границу с избытком, а правую с недостатком получим, что Т.е. среди 20 извлеченных камней не меньше 11 будут шлифованными.

Часто на практике приходиться решать обратную задачу, когда известно количество , а нужно определить сколько раз необходимо провести испытания.

Пример 4. В ящике лежат 100 шлифованных поделочных камня и 80 не шлифованных. Мастеру необходимо 11 шлифованных камней. Сколько камней, не выбирая, ему надо взять, чтобы среди взятых было нужное количество шлифованных камней?

Решение. Эта задача обратная задаче, рассмотренной в примере 3. Теперь известно , нужно найти . Для этого выполним простейшее преобразо-вание неравенства (3): отнимем от всех его частей и , получим

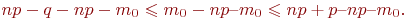
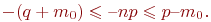
Умножим последнее неравенство на (- 1) и разделим на , тогда (при умножении на -1 знаки неравенства меняются на противоположные):

(4)

Воспользуемся полученной формулой (4) для решения нашего примера.

откуда

или

Округляя до целых, получим, что мастеру надо достать 19 либо 20 камней, чтобы среди них гарантиро-ванно было 11 шлифованных.

Пример 5. Вероятность попадания стрелка в цель равна 0,8. Стрелок делает 20 выстре-лов. определить наивероятнейшее количество попаданий.

Решение. Для решения задачи воспользуемся формулой (3):

откуда

Следовательно, стрелок скорее всего попадет 16 раз.

Если число испытаний большое, , а вероятность появления события при каждом испытании мала, , то для отыскания вероятности что при испытаниях некоторое событие случится раз используют приближенную формулу Пуассона, которая является обобщением формулы Бернулли:

(5)

где

(6)

Формулу ( 5) часто называют локальной теоремой Муавра-Лапласса.

Здесь функция . Существуют специальные таблицы, позволяющие вычислить значение данной функции по ее аргументу. На практике вычисляют 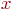, а затем по таблицам определяют значение функции. Если аргумент получился отрицательным, то значение функции будет такое же, как и при положительном аргументе. Т.е. .

Если вероятность появления события мала ( ), то для отыскания того, что испытание состоится раз, можно воспользоваться формулой Пуассона:

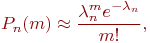
(7)

где - среднее число появления событий.

Если вероятность появления события меняется от испытания к испытанию, но сами испытания независимы, то тогда используется производящая функция , представляющая собой произведение вероятностных биномов. Эта функция обладает интересным свойством, которое просто проведем здесь без доказательства. После перемножения всех биномов и приведения подобных при коэффициенты при степенях 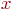представляют собой вероятность того, что событие появится раз в испытаниях, т.е.

(8)

Пример 6. Связь с шестью дальними партиями была организована через радио посред-ством радиостанций. Каждый отряд в течение дня имеет возможность в любое время связаться с базой, где радиостанция работает круглосуточно. Если вероятность связи с каждым из отрядов 0,8, найти вероятность того, что в данный момент не менее четырех партий вышли на связь.

Решение. Для решения задачи воспользуемся производящей функцией. Определим па-раметры функции: . Построим функцию

Сумма всех коэффициентов равна 1, в чем можно убедиться самостоятельно. По условию задачи нам не-обходимо учесть коэффициенты при членах . Тогда искомая вероятность будет равна

Пример 7. Два специалиста сортируют алмазы, которые затем собирают по размерам. Вероятность ошибки первого 0,1, а второго - 0,3. Из отсортированных алмазов одного размера взяли 2. Най-ти вероятность того, что оба алмаза будут одного размера.

Решение. Для решения задачи воспользуемся производящей функцией. Определим па-раметры функции: для первого специалиста .

Построим функцию: . По условию задачи нам необходимо учесть коэффициент при , т.е. искомая вероятность будет равна .

Пример 8. Статистикой установлено, что из каждой 1000 родившихся детей в среднем рождается 485 девочек, а остальные - мальчики. В семье 5 детей. Найти вероятность того, что среди этих детей: 3 мальчика.

Решение. Для решения задачи воспользуемся локальной теоремой Муавра – Лапласа, для которой определим необходимые переменные: .

Воспользуемся формулами (5) и (6): . Из таблицы находим значение функции

Теперь полученные значения подставим в формулу (5), получим:

Теорему Бернулли часто используют тогда, когда необходимо оценить вероятность наибольшего отклонения появления событий от ее ожидаемого значения. Случайной величиной в этом случае является число появлений событий и независимых испытаниях. В этом случае теорема Бернулли записывается так:

(9)

Пример 9. Из 1000 изделий, изготовленных цехом, проверили 200 случайно отобранных изделий. Среди них оказалось 25 изделий с браком. Приняв долю бракованных изделий среди отобранных за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии бракованных изделий окажется не более 10%.

Решение. Определим вероятность изготовления бракованного изделия: . Отклонение частости появлений бракованных изделий от вероятности по абсолютной величине равно Число испытаний 1000. Используем формулу (9) и находим искомую вероятность:

откуда - получаем ответ.