Функция распределения системы двух случайных величин

Функцией распределения системы двух случайных величин называется вероятность совместного выполнения двух неравенств 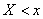и :

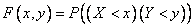. (8.2.1)

Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения есть не что иное, как вероятность попадании случайной точки в бесконечный квадрант с вершиной в точке , лежащий левее и ниже ее (рис. 8.2.1). В аналогичной интерпретации функция распределения одной случайной величины - обозначим ее - представляет собой вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой (рис. 8.2.2); функция распределения одной величины - вероятность попадания в полуплоскость, ограниченную ординатой у (рис. 8.2.3).

Рис. 8.2.1

В 5.2 мы привели основные свойства функции распределения 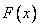для одной случайной величины. Сформулируем аналогичные свойства для функции распределения системы случайных величин и снова воспользуемся геометрической интерпретацией для наглядной иллюстрации этих свойств.

1. Функция распределения есть неубывающая функция обоих своих аргументов, т. е.

при ;

при .

В этом свойстве функции 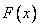можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадании в квадрант с вершиной (рис. 8.2.1). Действительно, увеличивая (смещая правую границу квадранта вправо) или увеличивая (смещая верхнюю границу вверх), мы, очевидно, не можем уменьшить вероятность попадания в этот квадрант.

Рис. 8.2.2 Рис. 8.2.3

2. Повсюду на функция распределения равна нулю:

.

В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта 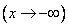или вниз его верхнюю границу или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.

3. При одном из аргументов, равном , функция распределил системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

,

где - соответственно функции распределения случайных, функция распределения величин и .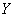

В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на ; при этом в пределе квадрант превращается в полуплоскость, вероятность попадания в которую есть функция распределения одной из величин, входящих в систему.

4. Если оба аргумента равны , функция распределения системы равна единице:

.

Действительно, при , квадрант с вершиной в пределе обращается во всю плоскость 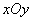, попадание в которую есть достоверное событие.

При рассмотрении законов распределения отдельных случайных величин (глава 5) мы вывели выражение для вероятности попадания случайной величины в пределы заданного участка. Эту вероятность мы выразили как через функцию распределения, так и через плотность распределения.

Аналогичным способом для системы двух случайных величин является вопрос о вероятности попадания случайной точки в пределы заданной области на плоскости 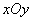(рис.8.2.4).

Рис. 8.2.4

Условимся событие, состоящие в попадании случайной точки в область , обозначать символом .

Вероятность попадания случайной точки в заданную область выражаются наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.

Выразим через функцию распределения системы вероятность попадания случайной точки в прямоугольник , ограниченный абсциссами и и ординатами и (рис. 8.2.5).

При этом следует условиться, куда мы будем относить границы прямоугольника. Аналогично тому, как мы делали для одной случайной величины, условимся включать в прямоугольник его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие будет равносильно произведению двух событий: и . Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости четыре бесконечных квадранта с вершинами в точках ; ; и (рис. 8.2.6).

Рис. 8.2.5. Рис. 8.2.6

Очевидно, вероятность попадания в прямоугольник равна вероятности попадания в квадрант минус вероятность попадания в квадрант минус вероятность попадания в квадрант плюс вероятность попадания в квадрант (так как мы дважды вычли вероятность попадании в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

. (8.2.2)

В дальнейшем, когда будет введено понятие плотности распределения системы, мы выведем формулу для вероятности попадания случайной точки в область произвольной формы.