
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
И решение экзаменационных задач
Подготовка к итоговой аттестации
И решение экзаменационных задач
Предисловие
Пособие даёт возможность систематизировать полученные знания и подготовиться к экзамену по алгебре и началам анализа за курс средней школы. В пособии рассмотрены основные темы дисциплины «Математика», показаны примеры оформления заданий, даны алгоритмы решения ряда задач.
Алгоритм решения любой задачи состоит из нескольких этапов, следуя которым, можно добиться успеха:
1) понять поставленную задачу;
2) восстановить в памяти необходимый теоретический материал, формулы;
3) составить план решения задачи;
4) решить задачу одним из способов, постаравшись выбрать оптимальный метод;
5) проверить результат решения.
Пособие адресовано выпускникам, решившим серьезно и вдумчиво подготовиться к выпускному экзамену, а также к вступительному экзамену в вуз.
Содержание
1. Предисловие………………………………………………………………1
2. Тригонометрические выражения……………………………………..…3
2.1 Рекомендации………………………………………………………….3
2.2 Примеры выполнения заданий………………………………………3
2.Тригонометрические уравнения…………………………………...4
2.1. Простейшие тригонометрические уравнения………………….4
2.3. Тригонометрические уравнения, сводящиеся к квадратным...5
2.4. Решение тригонометрических уравнений разложением на множители……………………………………………………………..6
2.6. Однородные тригонометрические уравнения…………………7
2.7 Системы тригонометрических уравнений………………………..8
3. Логарифмические выражения, уравнения, неравенства, системы…….8
2.1. Логарифмические выражения……………………………………….9
2.2. Логарифмические уравнения…………………………………………9
2.3. Логарифмические неравенства……………………………………..11
2.4. Системы логарифмических уравнений……………………………13
4. Показательная функция…………………………………………………13
3.1. Показательные уравнения………………………………………….14
3.2. Показательные неравенства………………………………………..16
3.3. Системы показательных уравнений……………………………….17
5. Степени……………………………………………………………………18
4.1. Упрощение выражений, содержащих степени……………………18
6. Иррациональные уравнения……………………………………………19
5.1. Рекомендации………………………………………………………..19
5.2. Решение уравнений, содержащих один радикал…………………19
5.3. Решение уравнений, содержащих два радикала…………………20
7. Некоторые способы решения уравнений и неравенств………………20
6.1. Алгоритм решения неравенств методом интервалов……………20
6.2. Примеры выполнения заданий…………………………………….20
8. Производная и ее применение………………………………………….23
7.1. Нахождение производной и ее значения в точке………………...23
7.2. Физический смысл производной…………………………………..24
7.3. Геометрический смысл производной……………………………..25
7.4. Касательная к графику функции…………………………………..26
7.5. Наибольшее и наименьшее значения функции…………………...28
9. Первообразная…………………………………………………………...29
8.1. Типовые задания по теме…………………………………………...29
8.2. Нахождение площади криволинейной трапеции…………………30
10. Справочный материал………………………………………………….31
Тригонометрические выражения
Рекомендации
Выполняя преобразования выражений, содержащих тригонометрические функции, пользуются свойствами алгебраических действий над тригонометрическими функциями и основными формулами тригонометрии.
Способ доказательства тригонометрических тождеств состоит в том, чтобы одну из его частей преобразовать с помощью тригонометрических и алгебраических операций таким образом, чтобы в результате получилось выражение, стоящее в другой части доказываемого тождества. Можно убедиться в совпадении левой и правой частей, преобразуя их в отдельности так, чтобы получились одинаковые выражения.
Необходимо внимательно следить, чтобы все преобразования выполнялись в области допустимых значений аргументов данного равенства.
Примеры выполнения заданий
Пример 1 (вариант 14 №3)
Найдите cos x, если sin x = -  ,
, 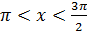 .
. 
Решение
Применим основное тригонометрическое тождество
sin2  + cos2
+ cos2  = 1,
= 1,
cos2  = 1 - sin2
= 1 - sin2  ,
,
cos2  = 1 – (
= 1 – (  )2 = 1 -
)2 = 1 -  =
=  ,
,
Так как  - угол III четверти, то cos
- угол III четверти, то cos  <0; получим cos
<0; получим cos  = -
= - 
Ответ: cos  = -
= - 
Пример 2 (вариант 44 №3)
Докажите тождество
sin4  - cos4
- cos4  + 2 cos2
+ 2 cos2  = 1.
= 1.
Преобразуем левую часть тождества, воспользовавшись формулой разности квадратов тригонометрических выражений.
sin4  - cos4
- cos4  + 2 cos2
+ 2 cos2 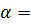 ( sin2
( sin2  - cos2
- cos2  )( sin2
)( sin2  + cos2
+ cos2  ) + 2cos2
) + 2cos2  = sin2
= sin2  - cos2
- cos2  + 2cos2
+ 2cos2  = sin2
= sin2  + cos2
+ cos2  = 1.
= 1.
1 = 1. Равенство верно для любых значений  Тождество доказано.
Тождество доказано.
Пример 3 (4.1)
Вычислите

Решение
 =
= 
= - 2sin 600 = -2  Ответ: -
Ответ: - 
2.
3.
Тригонометрические уравнения
Примеры выполнения заданий
Пример 1 (вариант 1 №3)
Найдите корни уравнения 2sin x + 1 = 0, принадлежащие отрезку [0; 2  ].
].
Решение
2sin x + 1 = 0,
sin x = -  ,
,
x = (-1)n arcsin(-  ) +
) +  ,
,
x = (-1)n (-  ) +
) +  ,
,
x = (-1)n+1  +
+  .
.
Из этих корней промежутку [0; 2  ] принадлежат
] принадлежат  и
и  так как
так как  ,
,
то n = 0; 
n = 0, x = (-1)1  +
+  [0; 2
[0; 2  ],
],
n = 1, x = (-1)2  +
+  [0; 2
[0; 2  ],
],
n = -1, x = (-1)0  -
-  [0; 2
[0; 2  ],
],
n = 2, x = (-1)3  +
+  [0; 2
[0; 2  ],
],
n = 3, x = (-1)4  +3
+3  [0; 2
[0; 2  ],
],
Ответ:  ;
;  .
.
Пример 2 (вариант 3 №3)
Решите уравнение
 +
+  .
.
Решение
Применим формулу приведения
 ,
,

 ,
,

Ответ:  .
.
Пример 3 (вариант 26 №3)
Решите уравнение  .
.
Решение


 ,
,

Ответ: 
Примеры выполнения заданий
Пример 1 (4.13)
Решите уравнение 2 
Решение
2 

2t2 – 3t +1 = 0;
D = 9 – 8 = 1>0;
 =
= 
1)  ,
,
x = (-1)n  +
+  .
.
2) 
 +
+ 
 (-1)n
(-1)n  +
+ 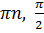 +
+  ,
, 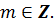
Пример 2 (4.1)
Решите уравнение

Решение

1 - 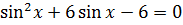 ,
,


t2 – 6t +5 = 0;
D = 36 – 20 = 16>0;


 +
+ 
 +
+ 
Пример 3 (5.1)
Решите уравнение -  =
=  .
.
Решение
-  =
=  ,
,
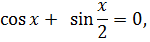
 +
+ 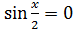
1 – 

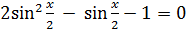 .
.
Обозначим 
2t2 –t – 1 = 0; D = 1 + 8 = 9,
t1 = 
1)  = -
= -  ,
,
 (-1)n+1
(-1)n+1  +
+  ,
,
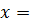 (-1)n+1
(-1)n+1  +
+  .
.
2)  ,
,
 +
+ 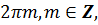

 (-1)n+1
(-1)n+1  +
+ 
 ,
, 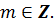
Пример 1 (4.27)
Решите уравнение
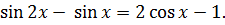
Решение

 ,
,

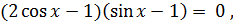

2)  +
+ 
Ответ:  +
+ 
Пример 2 (6.23)
Решите уравнение
1 + sin3x = 
Решение
1 + sin 3x = 
1 + sin3x = cos2  sin2
sin2 
1 + sin3x = 1 – sinx,
sin 3x + sin x = 0,
2sin 2x cos x = 0,
sin2x = 0, 2x 
cos x = 0, x =  +
+ 
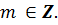
Ответ:  +
+ 
Пример 1( 4.35)
Найдите все решения уравнения  принадлежащих отрезку [-2
принадлежащих отрезку [-2 
Решение
 делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:
делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:

tg x = 1, x =  +
+ 

n = 0, x = 
 [-2
[-2 
n = 1, x = 
 [-2
[-2 
n = -1, x = 
 [-2
[-2 
n = -2, x = 
 [-2
[-2 
Ответ: 
Пример 2( 5.13)
Решите уравнение
6sin2 x + sin x cos x – cos2 x = 0.
Решение
6sin2 x + sin x cos x – cos2 x = 0, так как cos 2 x  0. То делим почленно на cos2 x
0. То делим почленно на cos2 x
6tg 2 x + tg x – 1 = 0.
Пусть tg x = t, тогда
6t 2 + t – 1 = 0; D = 1 + 24 = 25;
 =
= 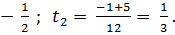
1) tg x = 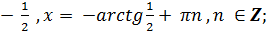
2) tg x = 
Ответ: 
Примеры выполнения заданий
Пример 1 (5.15)
Решите систему уравнений

Решение
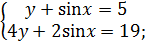

4y + 10 – 2y = 19,
2y = 9,
y = 4,5;


x = (-1)n  +
+  ;
;
Ответ: ( (-1)n  +
+  .
.
Справочный материал
Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить b, причем a >0, a ≠ 1, b > 0.
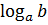 = c , (1)
= c , (1)

Логарифмическая функция
y= 
Свойства
1. D (y) = R+.
2. E(y) = R.
3. При a > 1 функция монотонно возрастает на R+ и при 0 <a <1 функция монотонно убывает наR+.
4. При x= 1 значение функции y = 0.
Логарифмические выражения
Примеры выполнения заданий
Пример 1 (4.58)
Вычислите

Решение

Ответ: 7.
Пример 2 (4.53)
Вычислите


Решение


Ответ: 2.
Логарифмические уравнения
Рекомендации
Решение логарифмических уравнений базируется на монотонности логарифмической функции  R+.
R+.
Примеры выполнения заданий
Пример 1 (вариант 17 №2)
Решите уравнение

Решение

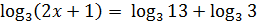
 D (
D (  R+;
R+;
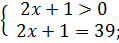

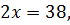
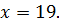

Пример 2 (4.91)
Решите уравнение

Решение
 D (
D (  R+;
R+;



 D>0;
D>0;

x1 = 1, x2 = 4.
Ответ: 1; 4.
Пример 3 (4.108)
Решите уравнение

Решение
 D (
D (  R+;
R+;

 ,
,
 ,
,
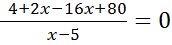 ,
,



 x = 6.
x = 6. 
Ответ: 6.
Пример 4 (6.7)
Решите уравнение
 -7) = 3 – x.
-7) = 3 – x.
Решение
 -7) =
-7) =  D (
D (  R+;
R+;




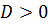 ; по теореме Виета
; по теореме Виета

 ) =R+,
) =R+,
Тогда 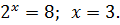
Ответ: 3.
Логарифмические неравенства
Рекомендации
Решение логарифмических неравенств базируется на монотонности логарифмической функции  При a > 1 функция монотонно возрастает на R+, а при 0 < a <1 функция монотонно убывает наR+.При решении неравенств необходимо учитывать условие, чтоD (
При a > 1 функция монотонно возрастает на R+, а при 0 < a <1 функция монотонно убывает наR+.При решении неравенств необходимо учитывать условие, чтоD (  R+.
R+.
Примеры выполнения заданий
Пример 1 (вариант 6 №2)
Решите неравенство


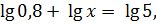
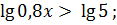
D (  R+;
R+; 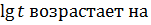 R+, т.к. 10 > 1, следовательно,
R+, т.к. 10 > 1, следовательно,

 x > 6,25.
x > 6,25. 
Пример 2 (4.93)
Укажите все целые решения неравенства

Решение

D (  R+;
R+;  R+, т.к. 4 > 1, следовательно
R+, т.к. 4 > 1, следовательно




 + _ +
+ _ +











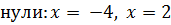 ;
;
-4 2
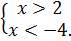













 + - +
+ - +
 ; -6 4
; -6 4 
















-6 -4 2 4
Целые решения: -5; 3.
Ответ: -5; 3.
Пример 3 (4.132)
Решите неравенство

Решение
Неравенство решим методом интервалов.
1) f(x)= 
Функция f(x) непрерывна на D(f).
2) D(f):

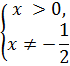

3) Нули f(x):

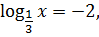
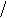

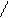

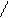
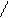
 + _
+ _





 = 9,
= 9, 

4) 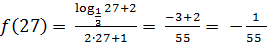 ,
,
 ,
, 
Ответ: 
Пример 1 (4.151)
Решите систему

Решение
D (  R+.
R+.


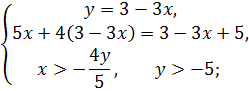
5x + 12 – 12x = 8 – 3x
12 - 8= 12x – 5x – 3x,
4 = 4, x =1, x >0; y = 3 – 3  0 > -5;
0 > -5;


Показательная функция.
Справочный материал
Определение.  н
н 
Свойства показательной функции
1. D (y) = R.
2.E(y) = R+.
3. При a > 1 функция монотонно возрастает на Rи при 0 <a <1 функция монотонно убывает наR.
4. При x= 0 значение функции y = 1.
5. Монотонность  используется при решении уравнений и неравенств.
используется при решении уравнений и неравенств.
3.1.
Показательные уравнения
Пример 3 (4.59)
Решите уравнение
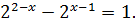
Решение

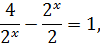
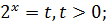
 1=0
1=0




 = -4,
= -4, 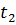 = 2;
= 2;
 = -4 не удовлетворяет условию
= -4 не удовлетворяет условию 
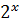 =2,
=2,
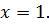
Ответ: 1.
Пример 4 (4.78)
Решите уравнение

Решение
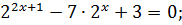
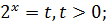
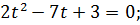
 −24=25>0,
−24=25>0,
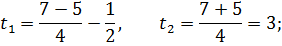
1) 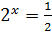 ,
, 
2) 
Ответ: 

Пример 5 (6.94)
Решите уравнение

Решение



D  ;
;
 = 2,
= 2, 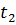 = 8;
= 8;
1) 
 = 1, x > 2,
= 1, x > 2,
x – 2 = 1,
x = 3.

 = 3, x > 2,
= 3, x > 2,
x – 2 = 9,
x =11.
Ответ: 3; 11.
Показательные неравенства
При решении показательных неравенств используется свойство монотонности показательной функции и ее возрастание и убывание в зависимости от значения основания.
Пример 1 (вариант 45 №2)
Решите неравенство

Решение


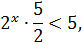

 чит меньшему значению функции соответствует меньшее значение аргумента.
чит меньшему значению функции соответствует меньшее значение аргумента.
x < 1.
Ответ:( 
Пример 2 (вариант 82 №2)
Решите неравенство

Решение



-3< 
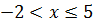 .
.
Ответ: ( 
Пример 3 (4.134)
Решите неравенство

Решение
Неравенство решим методом интервалов.
1. f (x) =  f (x) непрерывна на D( f ).
f (x) непрерывна на D( f ).
2. D( f ): 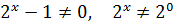 ,
, 
D( f )= 
+ _ +
3. 




 Нули:
Нули: 
0 9
4. f (1) = 

Ответ: 
Пример 1 (5.82)
Решите систему уравнений

Решение
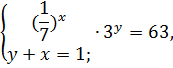




-x = 1,
x = -1;

Ответ: ( -1; 2).
Пример 2 (6.132)
Решите систему уравнений

Решение
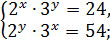

Разделим одно уравнение на другое:



x – y = 2,
x = 2 + y,


 =
= 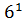 ,
,
y = 1;

Ответ: (3; 1).
Степени
Примеры выполнения заданий
Пример 1 (вариант 7 №1)
Вычислите

Решение

Ответ: 28.
Пример 2 (вариант 16 №1)
Упростите

Решение

Ответ: 
Пример 3 (вариант 40 №1)
Вычислите

Решение


Ответ: 10.
Пример 4 (вариант 66 №1)
Вычислите

Решение

Ответ: 
Пример 6 (вариант 81 №1)
Вычислите

Решение

Ответ: 1.
Иррациональные уравнения
Определение. Уравнение, содержащее иррациональное выражение относительно неизвестного, называется иррациональным.
Рекомендации
При решении иррациональных уравнений используются два основных метода:
1. Возведение обеих частей уравнения в одну и ту же степень.
2. Введение новых (вспомогательных) переменных.
При возведении обеих частей уравнения в одну и ту же степень могут появиться «посторонние» корни, поэтому при решении иррациональных уравнений необходима проверка найденных корней.
Пример 1 (5.35)
Решите уравнение
3x + 1 =  .
.
Решение
3x + 1 = 

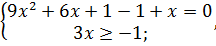




Пример 2 (5.53)
Найдите координаты общих точек графиков функций
y = 
Решение
Координаты искомых точек являются решением уравнения

Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...