
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Простейшие тригонометрические уравнения
При решении тригонометрических уравнений удобно пользоваться таблицей
Примеры выполнения заданий
Пример 1 (вариант 1 №3)
Найдите корни уравнения 2sin x + 1 = 0, принадлежащие отрезку [0; 2  ].
].
Решение
2sin x + 1 = 0,
sin x = -  ,
,
x = (-1)n arcsin(-  ) +
) +  ,
,
x = (-1)n (-  ) +
) +  ,
,
x = (-1)n+1  +
+  .
.
Из этих корней промежутку [0; 2  ] принадлежат
] принадлежат  и
и  так как
так как  ,
,
то n = 0; 
n = 0, x = (-1)1  +
+  [0; 2
[0; 2  ],
],
n = 1, x = (-1)2  +
+  [0; 2
[0; 2  ],
],
n = -1, x = (-1)0  -
-  [0; 2
[0; 2  ],
],
n = 2, x = (-1)3  +
+  [0; 2
[0; 2  ],
],
n = 3, x = (-1)4  +3
+3  [0; 2
[0; 2  ],
],
Ответ:  ;
;  .
.
Пример 2 (вариант 3 №3)
Решите уравнение
 +
+  .
.
Решение
Применим формулу приведения
 ,
,

 ,
,

Ответ:  .
.
Пример 3 (вариант 26 №3)
Решите уравнение  .
.
Решение


 ,
,

Ответ: 
Тригонометрические уравнения, сводящиеся к квадратным.
Чтобы овладеть методом решения, достаточно уметь решать квадратные уравнения и знать тригонометрические формулы.
Сам метод состоит в том, чтобы преобразовать уравнение к виду, позволяющему функцию  обозначить через новую переменную, получив при этом квадратное уравнение относительно t. Найдя значения, получим простейшее тригонометрическое уравнение.
обозначить через новую переменную, получив при этом квадратное уравнение относительно t. Найдя значения, получим простейшее тригонометрическое уравнение.
Примеры выполнения заданий
Пример 1 (4.13)
Решите уравнение 2 
Решение
2 

2t2 – 3t +1 = 0;
D = 9 – 8 = 1>0;
 =
= 
1)  ,
,
x = (-1)n  +
+  .
.
2) 
 +
+ 
 (-1)n
(-1)n  +
+ 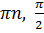 +
+  ,
, 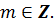
Пример 2 (4.1)
Решите уравнение

Решение

1 - 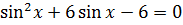 ,
,


t2 – 6t +5 = 0;
D = 36 – 20 = 16>0;


 +
+ 
 +
+ 
Пример 3 (5.1)
Решите уравнение -  =
=  .
.
Решение
-  =
=  ,
,
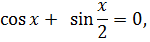
 +
+ 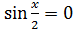
1 – 

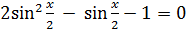 .
.
Обозначим 
2t2 –t – 1 = 0; D = 1 + 8 = 9,
t1 = 
1)  = -
= -  ,
,
 (-1)n+1
(-1)n+1  +
+  ,
,
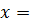 (-1)n+1
(-1)n+1  +
+  .
.
2)  ,
,
 +
+ 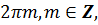

 (-1)n+1
(-1)n+1  +
+ 
 ,
, 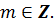
Решение тригонометрических уравнений разложением на множители
Данное выражение представляется в виде произведения нескольких сомножителей. В случае, когда выражение равно нулю, каждый из них приравнивается к нулю и уравнение сводится к более простому.
Пример 1 (4.27)
Решите уравнение
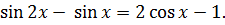
Решение

 ,
,

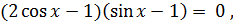

2)  +
+ 
Ответ:  +
+ 
Пример 2 (6.23)
Решите уравнение
1 + sin3x = 
Решение
1 + sin 3x = 
1 + sin3x = cos2  sin2
sin2 
1 + sin3x = 1 – sinx,
sin 3x + sin x = 0,
2sin 2x cos x = 0,
sin2x = 0, 2x 
cos x = 0, x =  +
+ 
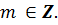
Ответ:  +
+ 
Однородные тригонометрические уравнения
Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным.
Его можно решать, выполнив деление на старшую степень косинуса (или синуса).
Пример 1( 4.35)
Найдите все решения уравнения  принадлежащих отрезку [-2
принадлежащих отрезку [-2 
Решение
 делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:
делим уравнение почленно на cosx ( заметим: если в данное уравнение подставить cosx =0, то получим sinx = 0, что невозможно, значит, в результате деления на cosx не будет потери корней) и находим:

tg x = 1, x =  +
+ 

n = 0, x = 
 [-2
[-2 
n = 1, x = 
 [-2
[-2 
n = -1, x = 
 [-2
[-2 
n = -2, x = 
 [-2
[-2 
Ответ: 
Пример 2( 5.13)
Решите уравнение
6sin2 x + sin x cos x – cos2 x = 0.
Решение
6sin2 x + sin x cos x – cos2 x = 0, так как cos 2 x  0. То делим почленно на cos2 x
0. То делим почленно на cos2 x
6tg 2 x + tg x – 1 = 0.
Пусть tg x = t, тогда
6t 2 + t – 1 = 0; D = 1 + 24 = 25;
 =
= 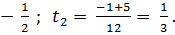
1) tg x = 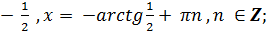
2) tg x = 
Ответ: 
Системы тригонометрических уравнений
Решение систем тригонометрических уравнений чаще всего сводится к решению алгебраических систем относительно sin x, cos x, tg x и т.п.
Необходимо отметить, что при решении простейших уравнений нужно писать различные целочисленные параметры n и k. Если бы мы использовали одну и ту же букву, было бы потеряно бесконечное множество решений.
Есть и иной способ решения систем, в котором может использоваться способ выражения одного переменного через другое и подстановка во второе уравнение.
Решение системы записывается в виде упорядоченных пар (x; y).
Примеры выполнения заданий
Пример 1 (5.15)
Решите систему уравнений

Решение
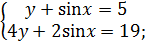

4y + 10 – 2y = 19,
2y = 9,
y = 4,5;


x = (-1)n  +
+  ;
;
Ответ: ( (-1)n  +
+  .
.
Логарифмические выражения, уравнения, неравенства, системы
Справочный материал
Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести a, чтобы получить b, причем a >0, a ≠ 1, b > 0.
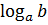 = c , (1)
= c , (1)

Основное логарифмическое тождество
 (2)
(2)

Логарифмическая функция
y= 
Свойства
1. D (y) = R+.
2. E(y) = R.
3. При a > 1 функция монотонно возрастает на R+ и при 0 <a <1 функция монотонно убывает наR+.
4. При x= 1 значение функции y = 0.
Логарифмические выражения
Примеры выполнения заданий
Пример 1 (4.58)
Вычислите

Решение

Ответ: 7.
Пример 2 (4.53)
Вычислите


Решение


Ответ: 2.
Логарифмические уравнения
Рекомендации
Решение логарифмических уравнений базируется на монотонности логарифмической функции  R+.
R+.
Примеры выполнения заданий
Пример 1 (вариант 17 №2)
Решите уравнение

Решение

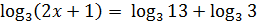
 D (
D (  R+;
R+;
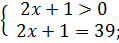

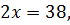
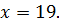

Пример 2 (4.91)
Решите уравнение

Решение
 D (
D (  R+;
R+;



 D>0;
D>0;

x1 = 1, x2 = 4.
Ответ: 1; 4.
Пример 3 (4.108)
Решите уравнение

Решение
 D (
D (  R+;
R+;

 ,
,
 ,
,
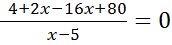 ,
,



 x = 6.
x = 6. 
Ответ: 6.
Пример 4 (6.7)
Решите уравнение
 -7) = 3 – x.
-7) = 3 – x.
Решение
 -7) =
-7) =  D (
D (  R+;
R+;




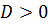 ; по теореме Виета
; по теореме Виета

 ) =R+,
) =R+,
Тогда 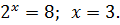
Ответ: 3.
Логарифмические неравенства
Рекомендации
Решение логарифмических неравенств базируется на монотонности логарифмической функции  При a > 1 функция монотонно возрастает на R+, а при 0 < a <1 функция монотонно убывает наR+.При решении неравенств необходимо учитывать условие, чтоD (
При a > 1 функция монотонно возрастает на R+, а при 0 < a <1 функция монотонно убывает наR+.При решении неравенств необходимо учитывать условие, чтоD (  R+.
R+.
Примеры выполнения заданий
Пример 1 (вариант 6 №2)
Решите неравенство


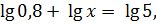
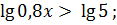
D (  R+;
R+; 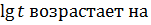 R+, т.к. 10 > 1, следовательно,
R+, т.к. 10 > 1, следовательно,

 x > 6,25.
x > 6,25. 
Пример 2 (4.93)
Укажите все целые решения неравенства

Решение

D (  R+;
R+;  R+, т.к. 4 > 1, следовательно
R+, т.к. 4 > 1, следовательно




 + _ +
+ _ +











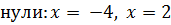 ;
;
-4 2
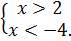













 + - +
+ - +
 ; -6 4
; -6 4 
















-6 -4 2 4
Целые решения: -5; 3.
Ответ: -5; 3.
Пример 3 (4.132)
Решите неравенство

Решение
Неравенство решим методом интервалов.
1) f(x)= 
Функция f(x) непрерывна на D(f).
2) D(f):

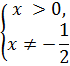

3) Нули f(x):

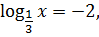
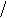

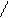

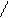
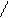
 + _
+ _





 = 9,
= 9, 

4) 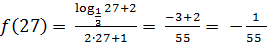 ,
,
 ,
, 
Ответ: 
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...