
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Системы логарифмических уравнений
Пример 1 (4.151)
Решите систему

Решение
D (  R+.
R+.


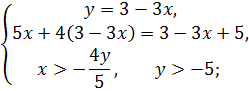
5x + 12 – 12x = 8 – 3x
12 - 8= 12x – 5x – 3x,
4 = 4, x =1, x >0; y = 3 – 3  0 > -5;
0 > -5;


Показательная функция.
Показательные уравнения, неравенства, системы.
Справочный материал
Определение.  н
н 
Свойства показательной функции
1. D (y) = R.
2.E(y) = R+.
3. При a > 1 функция монотонно возрастает на Rи при 0 <a <1 функция монотонно убывает наR.
4. При x= 0 значение функции y = 1.
5. Монотонность  используется при решении уравнений и неравенств.
используется при решении уравнений и неравенств.
3.1.
Показательные уравнения
Основные методы решения показательных уравнений
1. Приведение к одному основанию.
2. Вынесение за скобку общего множителя.
3. Логарифмирование обеих частей уравнения.
4. Использование монотонности функции.
5. Введение новой переменной.
Пример 1 (вариант 6 №2)
Решите уравнение

Решение

 -
- 
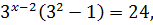

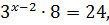

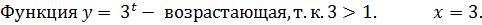

Пример 2 (вариант 47 №2)
Решите уравнение

Решение
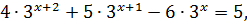





x = -2.
Ответ: -2.
Пример 3 (4.59)
Решите уравнение
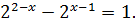
Решение

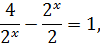
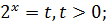
 1=0
1=0




 = -4,
= -4, 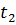 = 2;
= 2;
 = -4 не удовлетворяет условию
= -4 не удовлетворяет условию 
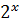 =2,
=2,
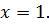
Ответ: 1.
Пример 4 (4.78)
Решите уравнение

Решение
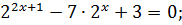
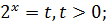
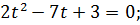
 −24=25>0,
−24=25>0,
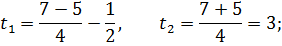
1) 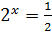 ,
, 
2) 
Ответ: 

Пример 5 (6.94)
Решите уравнение

Решение



D  ;
;
 = 2,
= 2, 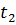 = 8;
= 8;
1) 
 = 1, x > 2,
= 1, x > 2,
x – 2 = 1,
x = 3.

 = 3, x > 2,
= 3, x > 2,
x – 2 = 9,
x =11.
Ответ: 3; 11.
Показательные неравенства
При решении показательных неравенств используется свойство монотонности показательной функции и ее возрастание и убывание в зависимости от значения основания.
Пример 1 (вариант 45 №2)
Решите неравенство

Решение


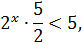

 чит меньшему значению функции соответствует меньшее значение аргумента.
чит меньшему значению функции соответствует меньшее значение аргумента.
x < 1.
Ответ:( 
Пример 2 (вариант 82 №2)
Решите неравенство

Решение



-3< 
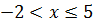 .
.
Ответ: ( 
Пример 3 (4.134)
Решите неравенство

Решение
Неравенство решим методом интервалов.
1. f (x) =  f (x) непрерывна на D( f ).
f (x) непрерывна на D( f ).
2. D( f ): 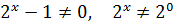 ,
, 
D( f )= 
+ _ +
3. 




 Нули:
Нули: 
0 9
4. f (1) = 

Ответ: 
Системы показательных уравнений
Пример 1 (5.82)
Решите систему уравнений

Решение
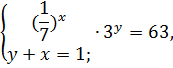




-x = 1,
x = -1;

Ответ: ( -1; 2).
Пример 2 (6.132)
Решите систему уравнений

Решение
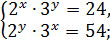

Разделим одно уравнение на другое:



x – y = 2,
x = 2 + y,


 =
= 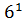 ,
,
y = 1;

Ответ: (3; 1).
Степени
Упрощение выражений, содержащих степени
Данные задания содержатся только в обязательной части и не представляют трудности для обучающихся.
Примеры выполнения заданий
Пример 1 (вариант 7 №1)
Вычислите

Решение

Ответ: 28.
Пример 2 (вариант 16 №1)
Упростите

Решение

Ответ: 
Пример 3 (вариант 40 №1)
Вычислите

Решение


Ответ: 10.
Пример 4 (вариант 66 №1)
Вычислите

Решение

Ответ: 
Пример 6 (вариант 81 №1)
Вычислите

Решение

Ответ: 1.
Иррациональные уравнения
Определение. Уравнение, содержащее иррациональное выражение относительно неизвестного, называется иррациональным.
Рекомендации
При решении иррациональных уравнений используются два основных метода:
1. Возведение обеих частей уравнения в одну и ту же степень.
2. Введение новых (вспомогательных) переменных.
При возведении обеих частей уравнения в одну и ту же степень могут появиться «посторонние» корни, поэтому при решении иррациональных уравнений необходима проверка найденных корней.
Решение уравнений, содержащих один радикал
Пример 1 (5.35)
Решите уравнение
3x + 1 =  .
.
Решение
3x + 1 = 

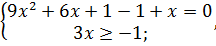




Пример 2 (5.53)
Найдите координаты общих точек графиков функций
y = 
Решение
Координаты искомых точек являются решением уравнения

 ;
;






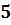 .3. Решение уравнений, содержащих два радикала
.3. Решение уравнений, содержащих два радикала
 Иногда попытка решения наталкивается на технические трудности, поэтому проще решить полученное уравнение и проверкой определить посторонние корни.
Иногда попытка решения наталкивается на технические трудности, поэтому проще решить полученное уравнение и проверкой определить посторонние корни.
Пример 1 (5.27)
Решите уравнение
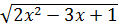 -
- 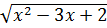 = 0.
= 0.
Решение
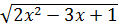 -
- 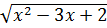 = 0,
= 0,
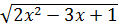 =
= 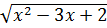 ;
;




1) 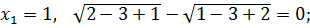

2)  = 0;
= 0;

0 = 0.
Ответ: -1; 1.
Некоторые способы решения уравнений и неравенств
Наряду с уравнениями и неравенствами, решаемыми традиционными методами, встречаются уравнения и неравенства, которые можно решать на основе монотонности функции.
Неравенства часто легче решать методом интервалов.
Алгоритм решения неравенств методом интервалов
1. Ввести функцию f(x), f(x) непрерывна на D(f).
2. Найти D(f).
3. Нули функции: f(x) = 0.
4. Нанести точки из D(f) и нули функции на числовую ось, f(x) сохраняет определенный знак на каждом из интервалов.
5. Определить знак в каждом интервале и записать ответ.
Примеры выполнения заданий.
Пример 1 (вариант 1 №1)
Решите неравенство



1) 

2)  −1
−1 

3)  x = 0,
x = 0, 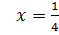 .
.
+ _ + _
4)
 |
0  1
1
f(2) = 
5) 

Пример 2 (вариант 28 №1)
Решите неравенство

Решение

1)  дробно-рациональная функция.
дробно-рациональная функция.
f(x) непрерывна на D(f).
2) D(f): x  .
.
3) Нули функции: 
 =8;
=8;
 =
=  .
.





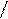





 _ + _ +
_ + _ +






 4)
4)
-2 - 

f(0) = 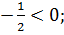
5) 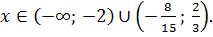
Ответ: 
Пример 3 (вариант 94 №1)
Найдите область определения функции
y =  .
.
Решение

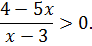
1) f(x)=  - дробно-рациональная функция; f(x) непрерывна на D(f).
- дробно-рациональная функция; f(x) непрерывна на D(f).
2) x – 3  x
x 
3) Нули: x =  .
.





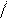

 _ + _
_ + _
4)
 | |||
 | |||
 3 x
3 x
f (4)<0;
x 
Ответ: 
Пример 4 (4.127)
Решите неравенство



1) f (x)=  непрерывна на D(f).
непрерывна на D(f).
2) D(f):

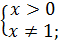

3) Нули: 3x – 4 = 0, x = 





 _ + _
_ + _
4)
 |  | ||
0 1 
 ) =
) = 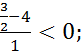
 .
.
Ответ:  .
.
Производная
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...