Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Моделирование простейшей одноканальной системы СМО
Понятие о моделировании.
Реальное явление – Представление человека об этом явлении- Модель явления -Предсказание- Сравнение с экспериментом – Уточнение модели
Модель- искусственный объект, созданный человеком, заменяющий реальный объект.
Если модель заменяет объект с достаточной точностью, то она адекватна. Адекватность инженерных моделей зависит от инжен-го опыта, интуиции и подготовки специалистов.
Основная задача модел-ия – построение таких моделей, которые позвол. выполнять исследования на них, а не на реальных объектов.
Системы массового обслуживания
Рассмотрим несколько примеров:
1. Портовый кран перегружает контейнеры с автотранспорта на корабль. Автомобили подвозят контейнеры через случайные промежутки времени. Какой случайный промежуток времени требуется на перемещение контейнера?
2. Имеется цех. С предыдущей технологической операции к нему поступают детали через произвольные промежутки времени. На обработку партии также требуется случайный промежуток времени.
3. Имеется стойка телефонной станции, на вход которой поступают вызовы абонентов. Через какой случайный промежуток времени поступают вызовы?
Во всех примерах имеется нечто общее. Можно выделить так называемые заявки, которые образуют поток. Первый пример – автомобили, подвозящие контейнеры, во втором – партии деталей, в третьем – телефонные звонки.
Обслуживающий аппарат (ОА) называется каналом. В первом примере – это портовый кран, во втором - цех, в третьем – стойка на телефонной станции.
В зависимости от соотношения производительности обслуживающего аппарата и интенсивности потока заявок может образовываться очередь. В простейшем случае эту ситуацию можно изобразить следующим образом:
| |||||||||
|
|
| |||||||



Рис. Схема простейшей системы массового обслуживания
Заметим, что СМО могут быть достаточно сложными: в них могут присутствовать несколько ОА–каналов. Обслуживание может вестись с учетом приоритетов заявок.
Основными показателями СМО являются:
1. Загрузка обслуживающих аппаратов.
2. Коэффициент простоя ОА:  (где
(где  - загрузка).
- загрузка).
3. Количество заявок, обслуженных за рассмотренный промежуток времени t (производительность).
4. Средняя и максимальная длина очереди.
5. Время пребывания заявки в очереди.
Понятно, что можно определенным образом построить модель, позволяющую вычислить эти характеристики. Основная задача при моделировании СМО – определить типы и количество обслуживающих аппаратов, а также их связь между собой (структуру СМО). Так, чтобы обеспечить максимальную требуемую производительность системы массового обслуживания при выполнении заданных ограничений (например, стоимость ОА).
Виды моделирования.
1) Натурное. При таком моделировании объект изготавливается в натуральную величину из тех же материалов, которые будут использоваться в реальной эксплуатации и к которому прикладывают воздействие, как можно ближе воспроизводящее реальную среду.
преимущества: точные результаты при точности измерительной аппаратуры;
недостатки: высокая стоимость проведения эксперимента,часто испытуемый объект приходит в негодность после испытания, невозможность применения его в нек. Случаях.
2) Полунатурное. Объект изготавливают либо в измененном масштабе, либо из другого материала, либо еще с каким-то существенным отличием от реального.
преимущества: достаточно наглядное представление результатов;
недостатки: сложность пересчета полученных результатов к реальным.
3) Аналоговое базир-ся на философском принципе единства мира, который в частности выражается в том, что явления и процессы разной природы могут описываться одинаковыми по виду уравнениями.
Преимущества: решение получается мгновенно;
Недостатки: сложность пересчета полученного решения к искомым переменным.
Математическое моделирование:в этом случае в качестве искусственного объекта заменяющего реальный выступает математический объект. Этот объект может иметь формулу ур-ий, матриц, графов и т.д. Последовательность этапов переходов к компьютерной модели.
Преимущество:
1)универсальность
Если модель создано параметрически то это позволяет исследовать поведение Реального объекта различных размеров, материалов и т.д.
2)простая переносимость из одной лаборатории в другую
3)Высокая точность получения результатов при адекватном построении моделей.
Недостатки:
Создание универсального ПО для исследования широкого класса объектов требует существенных материальных затрат(зачастую сотни человека лет)
Простейший поток событий




 Потоком событий называют последовательность однородных событий следующих одно за другим в следующие моменты времени.
Потоком событий называют последовательность однородных событий следующих одно за другим в следующие моменты времени.
 | |||||||||||
| |
|
|
| ||||||||
| |||||||||||
Такой поток событий можно изобразить как последовательность точек на числовой оси, которым соответствуют случайные моменты времени.
Поток событий стационарный если вероятность попадания того или иного числа событий на участок времени зависит только от длины этого участка и не зависит от того где на оси времени он расположен.
Поток без последствия – такой поток событий для которой для любых непересекающихся участков времени число событий попадающих на один из них не зависит, сколько событий попало на другой.
Поток событий ординарный – если вероятность попадания на участке времени малой длины двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на этот участок 1-го события.
Стационарность потока означает, что вероятность характера этого потока не должны меняться в зависим ости от времени. Например, интенсивность потока событий = математическому ожиданию числа событий в единицу времени должна оставаться постоянной для стационарного потока. На практике часто встречаются потоки событий, которые стационарны на ограниченном участке времени. Например, поток вызовов на телефонной станции в дневное время можем считать стационарным. В то же время этот же поток в течении суток стационарным уже не будет поскольку интенсивность вызовов в ночное время меньше. Отсутствие последействия в потоке означает, что событие появляется в последующие моменты времени независимо друг от друга. Например, поток пассажиров входящих в метро можно считать потоком без последствий, поскольку причины поездки 1-го пассажира не связаны с причинами другого. В то же время поток пассажир покидающих станцию метро уже не может считаться потоком без последействия поскольку большинство из них прибыли одним и тем же поездом. Ординарный означает ,что события приходят поодиночке а не парами , тройками и т.д. Поток клиентов в парикмахерскую – ординарный, а в ЗАГС – неординарный. Простейшим называется поток событий, который обладает свойствами стационарности ординарности и отсутствия последействия. Такие потоки играют существенную роль поскольку встречаются часто и кроме того на их основе могут быть получены потоки с другими свойствами.
Замкнутые СМО
Рассмотрим системы массового обслуживания, в которых интенсивность потока поступающих заявок зависит от состояния самих систем. Такие системы массового обслуживания называются замкнутыми.
Пусть система состоит из п каналов обслуживания и т источников заявок, т>п.
Предположим, что каждый источник порождает простейший поток заявок с интенсивностью  , причем источник не может посылать следующую заявку до завершения обслуживания своей предыдущей заявки (в этом и выражается замкнутость данной системы). Предположим также, что каждый канал порождает простейший поток обслуженных заявок с интенсивностью
, причем источник не может посылать следующую заявку до завершения обслуживания своей предыдущей заявки (в этом и выражается замкнутость данной системы). Предположим также, что каждый канал порождает простейший поток обслуженных заявок с интенсивностью 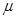 . Все состояния данной системы можно разбить условно на три группы:
. Все состояния данной системы можно разбить условно на три группы:
 - "все каналы свободны",
- "все каналы свободны",
 - "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
- "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
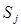 - "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ..., m.
- "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ..., m.
Графически все возможные переходы из состояния в состояние, а также интенсивности потоков событий, под воздействием которых эти переходы возможны, можно изобразить в виде размеченного графа так, как это показано на рис.2. Действительно, если система находится в состоянии  i = 0, 1,..., n - 1, то в состояние "i+ 1 каналов занято" она может перейти под воздействием суммарного потока заявок от m - i источников с интенсивностью
i = 0, 1,..., n - 1, то в состояние "i+ 1 каналов занято" она может перейти под воздействием суммарного потока заявок от m - i источников с интенсивностью  ; из состояния
; из состояния  в состояние
в состояние 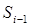 "i- 1 каналов занято" она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов обслуживания с интенсивностью
"i- 1 каналов занято" она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов обслуживания с интенсивностью 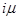 .. Напомним, что i источников прекращают поставку заявок до завершения обслуживания своих последних заявок. Если же система находится в состоянии
.. Напомним, что i источников прекращают поставку заявок до завершения обслуживания своих последних заявок. Если же система находится в состоянии 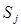 , j = n,...,m- 1, то в состояние
, j = n,...,m- 1, то в состояние  она может перейти под воздействием суммарного потока заявок с интенсивностью
она может перейти под воздействием суммарного потока заявок с интенсивностью  , а в состояние
, а в состояние  — под воздействием суммарного потока обслуженных заявок с интенсивностью
— под воздействием суммарного потока обслуженных заявок с интенсивностью  , поступающего от n каналов обслуживания.
, поступающего от n каналов обслуживания.

Рис. 2. Размеченный граф многоканальной замкнутой СМО
Составим на основе этого размеченного графа уравнения Колмогорова. Эти уравнения представляют собой систему линейных дифференциальных уравнений, описывающую вероятности Pr(t) нахождения данной системы в состоянии Sr в момент времени t, r = 0, 1, ..., m :
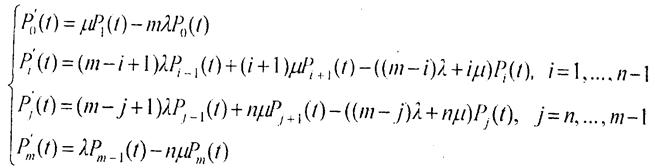
Особый интерес представляют вероятности Pr(t) в предельном стационарном режиме, т. е. при  , которые называются предельными вероятностями состояний системы.
, которые называются предельными вероятностями состояний системы.
Открытая СМО
Рассмотрим системы массового обслуживания, в которых интенсивность потока поступающих заявок не зависит от состояния самих систем. Такие системы массового обслуживания называются открытыми.
Пусть интенсивность простейшего потока поступающих заявок равна  и не зависит от состояния системы. Предполагается, что система состоит из п каналов обслуживания и каждый канал порождает простейший поток обслуженных заявок с интенсивностью
и не зависит от состояния системы. Предполагается, что система состоит из п каналов обслуживания и каждый канал порождает простейший поток обслуженных заявок с интенсивностью 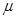 . Заявки, поступающие в момент, когда заняты все каналы, становятся в очередь ожидая обслуживания. Количество мест в очереди ограничено числом к : при наличии в очереди к заявок вновь поступающие заявки покидают систему необслуженными.
. Заявки, поступающие в момент, когда заняты все каналы, становятся в очередь ожидая обслуживания. Количество мест в очереди ограничено числом к : при наличии в очереди к заявок вновь поступающие заявки покидают систему необслуженными.
Все состояния данной системы можно разбить условно на три группы:
 - "все каналы свободны",
- "все каналы свободны",
 - "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
- "ровно i каналов занято и поступило ровно i заявок", i = 1, ..., n,
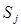 - "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ...,n+k .
- "все каналы заняты и ровно j-n заявок находятся в очереди для обслуживания", j = n + 1, ...,n+k .
Графически все возможные переходы из одного состояния в другое, а также интенсивности потоков событий, под воздействием которых эти переходы возможны, можно изобразить в виде размеченного графа так, как это показано на рис.23. Здесь m=n+k.

Рис.3. Размеченный граф многоканальной открытой СМО
Действительно, если система находится в состоянии  i = 0, 1,..., m, то в состояние
i = 0, 1,..., m, то в состояние 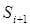 "i+ 1 каналов занято" она может перейти под воздействием потока заявок с интенсивностью
"i+ 1 каналов занято" она может перейти под воздействием потока заявок с интенсивностью  ;
;
Из состояния  в состояние
в состояние 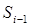 "i- 1 каналов занято" i = 1,..., n она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов, с интенсивностью
"i- 1 каналов занято" i = 1,..., n она может перейти под воздействием суммарного потока обслуженных заявок, поступающего от i каналов, с интенсивностью 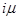 .
.
Из состояния 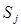 в состояние
в состояние  j = п + 1, ..., m, система может перейти под воздействием суммарного потока обслуженных заявок, поступающего от п каналов с интенсивностью
j = п + 1, ..., m, система может перейти под воздействием суммарного потока обслуженных заявок, поступающего от п каналов с интенсивностью  .
.
Составим на основе этого размеченного графа уравнения Колмогорова. Приравнивая производные нулю для стационарного случая, получим систему линейных алгебраических уравнений, описывающую предельные вероятности состояний системы:

Если мест в очереди не предусмотрено (k=0), то имеем частный случай открытой системы массового обслуживания. Графически этот случай описывается на рис. 4.
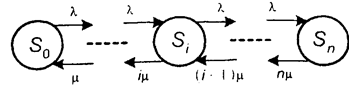
Рис.4. Размеченный граф многоканальной открытой СМО без очереди.
Для получения системы алгебраических уравнений, описывающей стационарный режим в этом случае, достаточно из последней системы удалить третий блок уравнений (при j = n,..., т- 1) и положить т = п.
Если рассматриваемая система массового обслуживания одноканальная, то из системы линейных алгебраических уравнений исключается второй блок уравнений; если система одноканальная и без очереди, то исключается второй и третий блоки уравнений.
Пусть система находится в предельном стационарном режиме. Тогда можно показать, что:
· вероятность Рот отказа заявке на обслуживание равна Рт ;
· вероятность Q принятия заявки на обслуживание равна 1- Рт ;
· среднее число А заявок, принимаемых системой на обслуживание в единицу времени, равно  Q;
Q;
· среднее число Nzan занятых каналов равно А/ 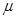 ;
;
· среднее число Noch заявок в очереди равно 
· среднее время tw ожидания заявки в очереди равно 
· среднее время tsys нахождения заявки в системе равно tw+ Q/ 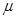 ;
;
Примеры задач приводящих к необходимости решения дифференциальных уравнений.
|









 Задача об определении изменения угла колебаний маятника.
Задача об определении изменения угла колебаний маятника.
|
|
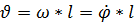


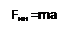 Спроектируем силы на касательной к траектории движекния
Спроектируем силы на касательной к траектории движекния



|

|

 (1)
(1)
Если малые колебания |  | << 1, то
| << 1, то 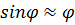
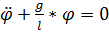 (2)
(2)
1 и 2 – Обыкновенные дифферинциальные уравнения 2-го порядка.
 Рассмотрим задачу об определении вида изогнутой оси балки
Рассмотрим задачу об определении вида изогнутой оси балки

|



 Вид сверху
Вид сверху
|
|













Пусть балка из материала с модулем Юнга E. Q(x) - непрерывная сила. М(x) – изгибающий момент.
y=y(x);
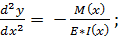
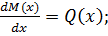
 I(x) = I – const;
I(x) = I – const;
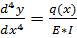 - обыкновенное дифферинциальное уравнение 4-го порядка
- обыкновенное дифферинциальное уравнение 4-го порядка
Понятие о конкурирующих стратегиях. Пример алгоритма для выбора рациональной стратегии.
Рассмотрим след. ситуацию.
В начале дня на маршрут выходит автобус, он полностью исправен, при выполнении рейса может возникнуть незначительная поломка при этом эту поломку можно устранить но для этого придется пропустить рейс а можно отпустить автобус в рейс с незначительной поломкой но приэтом может возникнуть критическая поломка когда автобус не сможет выполнять рейсы до конца дня. Пусть вероятность маленькой поломки «a», а критической «b».
Предположим в день запланировано n рейсов и всего должно быть m дней. Возникает вопрос какая из стратегий эксплуатации автобуса окажется лучшей, в том смысле что средн кол-во рейсов в день будет больше.
Эти стратегии называются конкурирующими. Очевидно что подобную задачу можно сформулировать и для др. объектов, напр, для металлообр станка. Впервые такая задача была сформулирована Крайзоном и Марзаном. С помощью сложных математических выкладок им удалось получить аналогичн решение этой задачи. Однако при небольшом усложнении условий или др формулир стратегий получать аналогичные решения практически не удается. В тоже время козе понятно что можно легко сформулир алгоритм и составить соотв прогр для моделирования этих стратегий на компьютере.
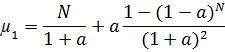
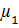 – среднее число рейсов в день при первой стратегии
– среднее число рейсов в день при первой стратегии
N – число запланированных рейсов
a – вер-ть незначительной поломки

 – среднее число рейсов при 2-й стратегии
– среднее число рейсов при 2-й стратегии
N –число запланированных рейсов
a – вероятность незначительной поломки
b – вероятность критической поломки
Равномерное приближение.

Понятно, что равномерное распределение выдвигает самое жесткое требование.
Примеры сведения дифференциальных уравнений и их систем произвольного порядка к системе ОДУ 1-го порядка в канонической форме Коши.

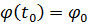
 - заданные числа.
- заданные числа.
Введем новые переменные 
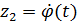


Исходное уравнение разрешим относительно старшей производной


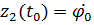
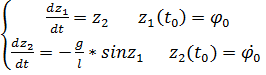
Пример 2:
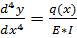 y(0) = y0 ; y’(0)= y’0 ; y”(0)=y0” ; y’’’(0)= y0’’’ – значения
y(0) = y0 ; y’(0)= y’0 ; y”(0)=y0” ; y’’’(0)= y0’’’ – значения
z1=y(x); z2=y’(x); z3=y”(x); z4=y’’’(x);

Пример решения задачи о колебаниях одно массовой системы на основе использования встроенной процедуры Rkadapt.

Пример использования разложения аппроксиматора по базисным функциям в виде мономов.
Пусть мы имеем функцию  на интервале
на интервале 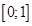 . Необходимо приблизить функцией
. Необходимо приблизить функцией  .
.
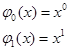
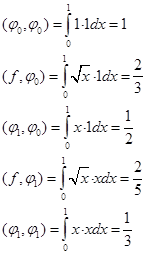
Тогда система уравнений (4) примет вид:
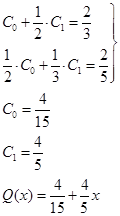
Пример получения математической модели для двух массовой колебательной системы
 q1 – линейное перемещение верхней массы
q1 – линейное перемещение верхней массы
q2 – нижней
q1, q2 – абсолютное перемещение (от земли)
 -уровень земли
-уровень земли
Выразим удлинение упругих элементов конструкции  и
и  Найдём:
Найдём:

Пример документа MathCad реализующий поточечную среднеквадратичную аппроксимацию
| поточечная среднквадаичная аппроксимция |

|

|

|
| x и y координаты узлов |

|
| длина массива x |
| Cистема базисных фукций |
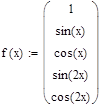
|

|

|

|
 
|
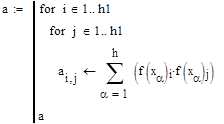

| Вычисление коэф на основе функции Minimize пример для функции 2ух пременных |

|
| x и y координаты узлов |

|

|
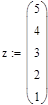
|

|
| базисные |
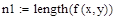
|

|

|

|
| начальное зачение для неизв коэф |

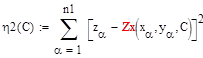

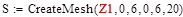
14.1 Некоторые примеры MathCad для решения различных задач

14.2 Остаточный член формулы Лагранжа, пример оценки точности интерполирования с использованием остаточного члена
Интерполяционная формула Лагранжа это один из наиболее распространенных способов построения интерполяционного полинома. Пусть имеем функцию:

 зависит от расположения узлов на интервале интерполирования. Для сравнения приведем значения и соответствующей таблицы: ln(2,5)=0,9163.
зависит от расположения узлов на интервале интерполирования. Для сравнения приведем значения и соответствующей таблицы: ln(2,5)=0,9163.
Пусть f(x) – интерполируемая функция. Заменим эту функцию полиномом Лагранжа: f(x)=Ln-1+R(f,x). R(f,x) – остаточный член формулы Лагранжа, который представляет собой погрешность метода интерполяции. При выполнения вычисления, результаты отдельных арифметических операций округляются или отсекаются из разряда, поэтому при построении интерполяционного полинома кроме погрешности метода будет присутствовать еще вычислительная погрешность. Можно доказать следующие утверждение: если функция f(x) n раз непрерывно дифференцируема на отрезке [a,b], содержащем узлы интерполирования x1, x2, …., xn, то  такая что
такая что  , где wn(x)=
, где wn(x)=  . Пусть Mn=
. Пусть Mn=  ,
,  . Понятно, чтобы использовать эту теорему нужно иметь возможность взять производную
. Понятно, чтобы использовать эту теорему нужно иметь возможность взять производную 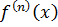 . Интерполяционный полином можно построить единственным образом по данным таблицы. Остаточный член R(f,x) всегда имеет один и тот же вид.
. Интерполяционный полином можно построить единственным образом по данным таблицы. Остаточный член R(f,x) всегда имеет один и тот же вид.
Модификации метода Эйлера
|


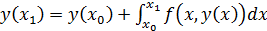
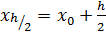

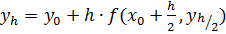 Можно показать, что погрешность этой ф-лы –
Можно показать, что погрешность этой ф-лы –  – метод 2-го порядка. Точность увеличивается на порядок, но приходится ещё раз обращаться к правой части ДУ
– метод 2-го порядка. Точность увеличивается на порядок, но приходится ещё раз обращаться к правой части ДУ
Численное интегрирование
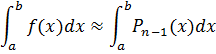
Т.е. подинтегрированную функцию f(x) заменяют интерполяционным полиномом, а затем от него вычисляется определенный интеграл. Операция приближенного интегрирования основана на этом подходе достаточна точна.
 Тоже справедливо и для функций заданных таблично:
Тоже справедливо и для функций заданных таблично:
Численное дифференцирование

К сожалению эта операция имеет приближенную точность:
Численное решение

алгебраических и тангенциальных уравнений:
Пусть исходная функция f(x) задана аналитически на интервале [a,b] и её значения могут быть вычислены в нужных точках. Пусть f(x)=0 – корень этого уравнения уединен на интервале [a,b], тогда по значениям этой функции в узлах строят интерполяционный полином, находят его корень на этом интервале и считают, что он приблизительно равен корню уравнения на этом интервале.
Методы 1-го порядка точности.
Пусть q=0 тогда А0 тогда  после вычисления
после вычисления 
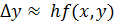
y(x+h) 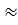 y(x)+hf(x,y) Мы получим формулу метода Эйлера, это значит что частный случай метода Рунге-Кутта.
y(x)+hf(x,y) Мы получим формулу метода Эйлера, это значит что частный случай метода Рунге-Кутта.
Понятие о сплайнах
Функция Sn,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если
1) на каждом из отрезков (xi, xi+1) из (a,b) функция Sn,ν (x) является полиномом степени n;
2) если Sn,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка
n- ν включительно.
Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах____
Рассмотрим сплайн 1-ой степени S1(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (xi, xi+1) он является полиномом 1-ой степени:
S1 (x) = A0+A1∙x
ν=1, т.е. непрерывной производной он не имеет.
Уравнение сплайна:
S1(x) = 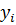 +
+ 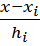 (
(  ), xi
), xi  i+1
i+1
hi =xi+1 – xi - шаг
Для построения этого сплайна требуется только таблица (xi ,yi). Вычисление этого сплайна можно выполнять по следующему алгоритму:
1) определение tg угла наклона:
tgαi =  =
= 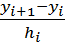
и вычисляется S1 (x)= 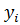 +Ui ∙ (x – xi ).
+Ui ∙ (x – xi ).
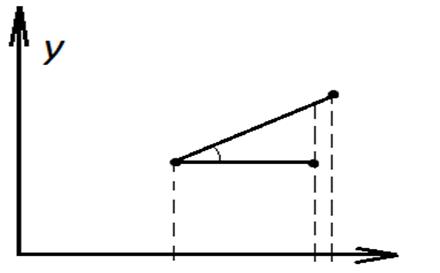
 (xi+1,yi+1)
(xi+1,yi+1)

 Ui(x-xi)
Ui(x-xi)
 (xi,yi) α
(xi,yi) α
S1(x)
yi
xi x xi+1
Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.
20.1 Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода 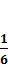 и их реализация в среде MathCad
и их реализация в среде MathCad
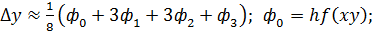
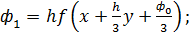
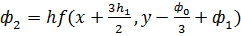 ;
; 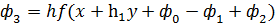
___________________________________________________________________________
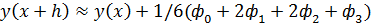
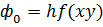
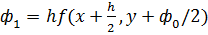
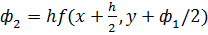
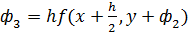
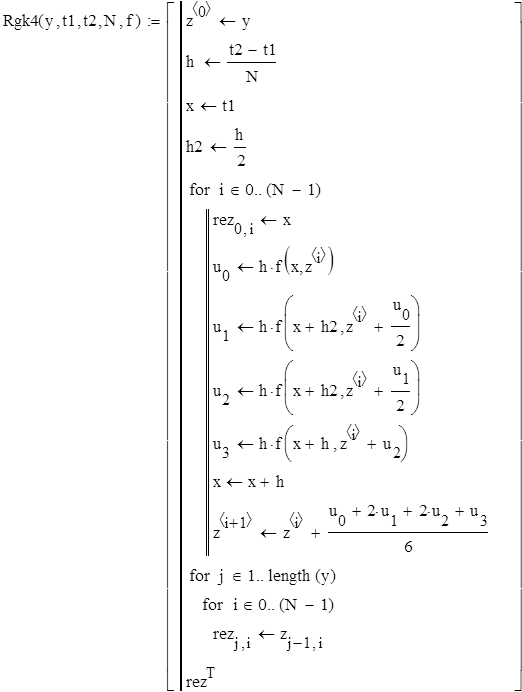
|
20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна
Функция Sn,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если
3) на каждом из отрезков (xi, xi+1) из (a,b) функция Sn,ν (x) является полиномом степени n;
4) если Sn,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка
n- ν включительно.
Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах____
Рассмотрим сплайн 1-ой степени S1(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (xi, xi+1) он является полиномом 1-ой степени:
S1 (x) = A0+A1∙x
ν=1, т.е. непрерывной производной он не имеет.
Уравнение сплайна:
S1(x) = 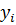 +
+ 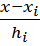 (
(  ), xi
), xi  i+1
i+1
hi =xi+1 – xi - шаг
Для построения этого сплайна требуется только таблица (xi ,yi). Вычисление этого сплайна можно выполнять по следующему алгоритму:
2) определение tg угла наклона:
tgαi =  =
= 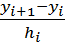
и вычисляется S1 (x)= 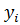 +Ui ∙ (x – xi ).
+Ui ∙ (x – xi ).

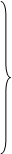 (xi+1,yi+1)
(xi+1,yi+1)

 Ui(x-xi)
Ui(x-xi)
 (xi,yi) α
(xi,yi) α
S1(x)
yi
xi x xi+1
Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.
Метод стрельбы
Пусть им
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...