
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Криволинейный интеграл 1-го рода. Сведение криволинейного интеграла 1-го рода к интегралу по отрезку.
Пусть в плоскости  задана кривая γ, т.е. образ непрерывной, взаимно однозначной вектор- функции:
задана кривая γ, т.е. образ непрерывной, взаимно однозначной вектор- функции:
 .
.
Пусть A= 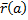 , B=
, B=  . Предположим, что кривая γ спрямляема. Рассмотрим, разбиение кривой γ точками
. Предположим, что кривая γ спрямляема. Рассмотрим, разбиение кривой γ точками  , таким что
, таким что 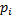 принадлежит дуге
принадлежит дуге  . Через
. Через  обозначим длину дуги
обозначим длину дуги  . Пусть на кривой γ задана функция f=f(M), где M принадлежит γ. Выберем на каждой дуге
. Пусть на кривой γ задана функция f=f(M), где M принадлежит γ. Выберем на каждой дуге
 точку
точку  и составим сумму
и составим сумму  .
.

Определение:
Если существует величина  , где
, где  , а придел не зависит от разбиения и от выбора точек {
, а придел не зависит от разбиения и от выбора точек {  } , то функция f(M) называется интегрируемой по кривой γ, а значение предела называется криволинейным интегралом I рода и обозначается через
} , то функция f(M) называется интегрируемой по кривой γ, а значение предела называется криволинейным интегралом I рода и обозначается через 
Замечание:В данном определении не играет никакой роли направление , которое может быть указано на γ.
Пусть M принадлежит γ. Тогда точке M соответствует единственное число s, равное длине дуги 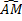 ,т.е (x(s),y(s))=M. Рассмотрим интегральную сумму :
,т.е (x(s),y(s))=M. Рассмотрим интегральную сумму :

где  – длина дуги
– длина дуги  , если
, если  - длина дуги
- длина дуги  , то получаем:
, то получаем:

Интегральная сумма в определении криволинейного интеграла совпадает с интегральной суммой функции
f(x(s),y(s))по отрезку [0,| γ|] , где | γ| -длина γ. Следовательно существование одного из интегралов влечет существование другого . В силу данного равенства получаем: 
Пусть функции φ(t),ψ(t) непрерывно дифференцируемы и (φ(t),ψ(t)) взаимно однозначное отображение, т. е. каждому значению t  [a, b] соответствует единственная точка M
[a, b] соответствует единственная точка M  γ, и обратно, для любой точки M
γ, и обратно, для любой точки M  γ существует единственное t
γ существует единственное t  [a, b] такое, что M=(φ(t),ψ(t)). Из условия на функции φ(t),ψ(t) следует, что γ является спрямляемой.
[a, b] такое, что M=(φ(t),ψ(t)). Из условия на функции φ(t),ψ(t) следует, что γ является спрямляемой.
Пусть s(t)- длина дуги 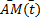 , M(t)= (φ(t),ψ(t)).
, M(t)= (φ(t),ψ(t)).
Тогда  , если возрастание параметра t соответствует возрастанию параметра s. Тогда
, если возрастание параметра t соответствует возрастанию параметра s. Тогда

.
 Вопрос 19.
Вопрос 19.
/*Обозначение Δ-треугольник . 
Пусть на плоскости  с декартовыми координатами (x,y) заданы кривая j , тюе образю вектор-функции:
с декартовыми координатами (x,y) заданы кривая j , тюе образю вектор-функции:


Которая является взаимно-однозначной и непрерывной. Будем считать, что кривая j является спрямляемой. Рассмотрим разбиение отрезка [a,b] точками a=  =b. обозначим через
=b. обозначим через  .
.  -дуга кривой j, расположенная между
-дуга кривой j, расположенная между  и
и  . Длина дуги обозначим через
. Длина дуги обозначим через
На каждой дуге  выберем произвольную точку A
выберем произвольную точку A 
 .*/
.*/
Пусть задана кривая γ на плоскости. Будем говорить, что γ ориентирована, если определено начало кривой и конец. Пусть A-начало γ, B-конец. Составим интегральные суммы:
 , Δ
, Δ 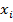 =
= 
 , Δ
, Δ  =
= 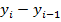 где
где  координаты точки
координаты точки 
Определение. Если 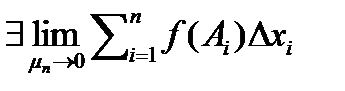 ,
,  , независящий от выбора разбиения кривой γ, то функция f называется интегрируемой по кривой, а значения таких пределов называют криволинейными интегралами 2-го рода и обозначают :
, независящий от выбора разбиения кривой γ, то функция f называется интегрируемой по кривой, а значения таких пределов называют криволинейными интегралами 2-го рода и обозначают :

Если заданы функции P(x,y), Q(x,y) на кривой γ, то выражение
 ,также называется интегралом второго рода.
,также называется интегралом второго рода.
Замечание. Справедливо следующее свойство. Пусть AB-кривая γ с началом в точке А и концом в точке В, а ВА –кривая γ с началом в точке В и конец А. Тогда 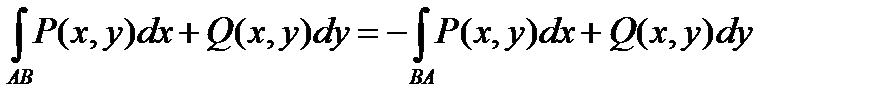 .
.
Теорема. Пусть кривая γ задана вектор-функцией  , где
, где  а функция f(x,y) непрерывна на γ. Пусть, кроме того,
а функция f(x,y) непрерывна на γ. Пусть, кроме того,
1)функции  непр. диф-мы на [a,b].
непр. диф-мы на [a,b].
2)  != 0
!= 0 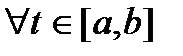
Если (φ(a),ψ(b))=A, (φ(b),ψ(b))=B, то
Тогда  .
.
Доказательство. Обозначим  . Зафиксируем
. Зафиксируем 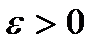 .Тогда существует
.Тогда существует  ,такое, что для всех разбиений Р отрезка [a,b] a=
,такое, что для всех разбиений Р отрезка [a,b] a=  =b, для которых
=b, для которых
μ(Р)=  <δ и всех точек
<δ и всех точек 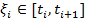 выполнено неравенство
выполнено неравенство
 ,
,
Где Δ 
Отметим что функция  , является непр. на [a,b] , то она равномерно непрерывна на [a,b].Следовательно,
, является непр. на [a,b] , то она равномерно непрерывна на [a,b].Следовательно, 
 , так что
, так что  |
|  |<
|<  , выполнено
, выполнено  . Рассмотрим разбиение
. Рассмотрим разбиение 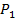 , для которого
, для которого 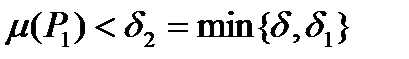 . Тогда :
. Тогда :

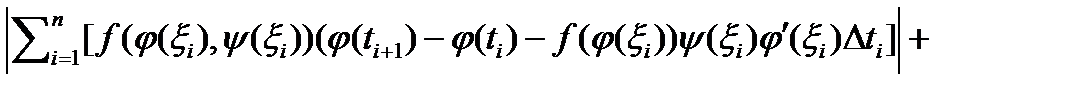 +
+ 
≤ 
По теореме Лагранжа о конечных приращениях 
 , так что
, так что  .
.
Тогда используя |  |<
|<  получаем
получаем

 ≤
≤
≤ 
Таким образом существует 
Что и доказывает утверждение теоремы.
6. Формула Грина. Выражение площади через криволинейный интеграл.
Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

с непрерывными частными производными первого порядка  . Тогда справедлива формула Грина
. Тогда справедлива формула Грина

где символ  указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.
указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.
Если  , то формула Грина принимает вид
, то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C.
Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля.
Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля  называется вектор, обозначаемый
называется вектор, обозначаемый  или
или  и равный
и равный
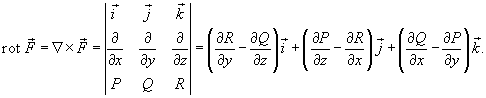
Формула Грина в векторной форме записывается в виде

Выражение площади плоской области через криволинейный интеграл. Из формулы Грина  следует неожиданный результат: если функции Р и Q удовлетворяют условию
следует неожиданный результат: если функции Р и Q удовлетворяют условию  , то
, то  (
( 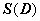 - площадь области D). Таким образом, площадь области можно выразить через криволинейный интеграл второго рода по границе этой области. В качестве функций Р и Q можно взять любые непрерывно дифференцируемые функции, такие что
- площадь области D). Таким образом, площадь области можно выразить через криволинейный интеграл второго рода по границе этой области. В качестве функций Р и Q можно взять любые непрерывно дифференцируемые функции, такие что  , например,
, например,  ;
;  ;
; 
 и т.д. В результате
и т.д. В результате  и т.д. При этом контур С (граница области D) обходится в положительном направлении. Чаще всего применяется третья из этих формул. Для примера найдём площадь, ограниченную эллипсом
и т.д. При этом контур С (граница области D) обходится в положительном направлении. Чаще всего применяется третья из этих формул. Для примера найдём площадь, ограниченную эллипсом  . Параметрические уравнения эллипса
. Параметрические уравнения эллипса  , поэтому:
, поэтому:
 ;
;
2. Поверхностный интеграл 1-го рода. Сведение поверхностного интеграла 1-го рода к двойному интегралу.
Поверхностный интеграл первого рода является таким же обобщением двойного интеграла, как криволинейный интеграл первого рода по отношению к определённому интегралу. 
Пусть S - поверхность в трёхмерном пространствеOxyz, а F(x,y,z) - непрерывная функция, определённая в точках этой поверхности. Поверхность S сетью линий разобьём на n участков ΔS1, ΔS2, ...., ΔSi, ..., ΔSn, не имеющих общих внутренних точек (рис. 3.8). Площади "элементарных" участков обозначим теми же буквамиSi(i = 1,...,n), а наибольший из диаметров этих участков - через λ На каждом "элементарном" участке ΔSiпроизвольным образом выберем по точке Mi(xi,yi,zi) (i = 1,...,n) и составим сумму

которая называется интегральной суммой для функции F(x,y,z) по поверхности S.
Определение 3.3. Если существует конечный предел

не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек Mi  ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается
ΔSi(i=1,....n), то он называется поверхностным интегралом первого рода от функции f(x,y,z) по поверхности S и обозначается

Поверхностный интеграл обладает всеми обычными свойствами интеграла, включая теорему о среднем значении.
Приведём простейшие достаточные условия существования поверхностного интеграла первого рода.
Теорема 3.4. Если поверхность S задана уравнением z = f(x,y), где функция f(x,y) и её частные производные f'x(x,y) и f'y(x,y) непрерывны в замкнутой области τ (τ - есть область, в которую проектируется поверхность S на координатную плоскость Oху), а функция F(x,y,z)непрерывна на S, то интеграл

существует.
К использованию этих условий, равно как и условий, получающихся из них перестановкой переменных x, y, z сводится большинство практически встречающихся случаев.
Вычисление поверхностных интегралов первого рода обычно производится путём их сведения к двойным интегралам.
Пусть выполнены все условия приведенной выше теоремы, тогда, обозначив проекцию ΔSi(и площадь проекции) на плоскость Oxy через Δτi, по теореме о среднем значении будем иметь:
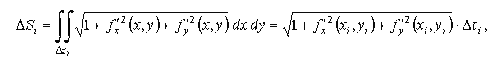
где (xi, yi)  Δτi, а, следовательно
Δτi, а, следовательно

при данном специфическом выборе точек Mi. Но сумма, стоящая справа, в последнем интеграле есть интегральная сумма для функции

по плоской области τ. Переходя к пределу, получаем:
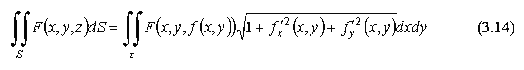
Если проектировать поверхность S не на координатную плоскость Oxy, а на координатную плоскость Oxz или Oyz, то можно записать формулы для вычисления поверхностного интеграла аналогично формуле (3.14).
Приложения поверхностного интеграла различны. Так, например:
1) если положить F(x,y,z)=1, то интеграл (3.12) будет численно равен площади поверхности S.
2) если же функцию F(x,y,z) интерпретировать как плотность вещества, распределенного по поверхности S, то интеграл (3.12) численно равен массе материальной поверхности S.
Пример 3.9. Вычислить
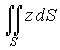
где S - поверхность конуса

при 1 ≤ z ≤ 2 (рис. 3.9).

Решение
Очевидно, что поверхность S проектируется на плоскость Oxy в кольцо τ: 1 ≤ х2 + у2 ≤ 4.
В области τ функция
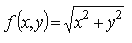
и её производные
 и
и  есть непрерывные функции.
есть непрерывные функции.
Следовательно,

3. Ориентация поверхностей. Поверхностный интеграл 2-го рода. Сведение поверхностного интеграла 2-го рода к двойному интегралу
Рассмотрим кусок гладкой поверхности  , определяемый векторным уравнением
, определяемый векторным уравнением
 , (1)
, (1)
где функции 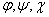 - непрерывно дифференцируемые на замыкании
- непрерывно дифференцируемые на замыкании  области
области  с кусочно-гладкой границей и
с кусочно-гладкой границей и
 . (2)
. (2)
Как всегда, мы предполагаем, что имеет место взаимно однозначное соответствие  между точками
между точками 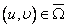 и точками
и точками  .
.
Единичная нормаль в произвольной точке  определяется по формуле
определяется по формуле
 . (3)
. (3)
Знаку «+» соответствует одна сторона поверхности  со щеткой выпущенных в ее сторону единичных нормальных векторов, непрерывно зависящих от
со щеткой выпущенных в ее сторону единичных нормальных векторов, непрерывно зависящих от  , а знаку «-» - другая сторона
, а знаку «-» - другая сторона  .
.
Дадим определение. Если из каждой точки  гладкой поверхности
гладкой поверхности  можно выпустить единичную нормаль
можно выпустить единичную нормаль  так, что полученная векторная функция от
так, что полученная векторная функция от  будет непрерывной на всей поверхности
будет непрерывной на всей поверхности  , то
, то  называется ориентируемой поверхностью.
называется ориентируемой поверхностью.
Функцию  называют еще непрерывным полем нормалей.
называют еще непрерывным полем нормалей.
Поверхность, для которой определена такая функция  , называется ориентированной при помощи
, называется ориентированной при помощи  . Если мы говорим, что
. Если мы говорим, что  есть ориентированная поверхность, то тем самым считаем, что
есть ориентированная поверхность, то тем самым считаем, что  обозначает не только поверхность (множество точек), но и тот факт, что на ней задана указанная непрерывная на
обозначает не только поверхность (множество точек), но и тот факт, что на ней задана указанная непрерывная на  функция
функция  . Говорят еще, что
. Говорят еще, что  задает определенную сторону ориентированной гладкой поверхности (куда выходит из
задает определенную сторону ориентированной гладкой поверхности (куда выходит из  щетка единичных векторов
щетка единичных векторов  , непрерывно зависящих от
, непрерывно зависящих от  ).
).
Ту же поверхность, но ориентированную противоположным образом (щеткой единичных нормальных векторов, идущих в противоположном направлении) надо уже обозначать другой буквой. Две такие противоположно ориентированные поверхности удобно обозначать буквами  и
и  . Одна из них произвольно обозначается через
. Одна из них произвольно обозначается через  , а другая автоматически получает обозначение
, а другая автоматически получает обозначение  .
.
Простейшим примером ориентируемой поверхности является плоскость  . Единичные векторы, перпендикулярные плоскости и идущие в положительном направлении оси
. Единичные векторы, перпендикулярные плоскости и идущие в положительном направлении оси  , определяют одну сторону плоскости, а векторы, идущие в отрицательном направлении оси
, определяют одну сторону плоскости, а векторы, идущие в отрицательном направлении оси  , - другую сторону плоскости
, - другую сторону плоскости  .
.

Рис. 88
Поверхность эллипсоида также ориентируема - выпущенный из какой-либо ее точки единичный вектор нормали во внешность эллипсоида, очевидно, непрерывно продолжается (однозначно!) на всю поверхность.
Этим поверхность ориентирована (определена внешняя сторона эллипсоида).
Другая, противоположная, ориентация этой поверхности определяется единичным нормальным к ней вектором, идущим внутрь эллипсоида (внутренняя сторона эллипсоида).
Выше мы видели, что если  есть гладкая поверхность, определенная параметрическими уравнениями (1) с указанными там свойствами, то она ориентируема. Знаку «+» в формуле (3) соответствует определенная ориентация
есть гладкая поверхность, определенная параметрическими уравнениями (1) с указанными там свойствами, то она ориентируема. Знаку «+» в формуле (3) соответствует определенная ориентация  , а знаку «-» будет тогда соответствовать противоположная ориентация.
, а знаку «-» будет тогда соответствовать противоположная ориентация.
Вообще же существуют гладкие поверхности не ориентируемые.
Если прямоугольный лист 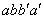 (рис. 88) перекрутить один раз и его стороны
(рис. 88) перекрутить один раз и его стороны  склеить так, чтобы точки
склеить так, чтобы точки  и
и  склеились попарно, то получим не ориентируемую поверхность (рис. 89), называемую листом Мёбиуса.
склеились попарно, то получим не ориентируемую поверхность (рис. 89), называемую листом Мёбиуса.
На рис. 88 отмечен отрезок  - средняя линия прямоугольного листа бумаги. Этой линии на листе Мёбиуса соответствует замкнутая кривая
- средняя линия прямоугольного листа бумаги. Этой линии на листе Мёбиуса соответствует замкнутая кривая  , у которой точки
, у которой точки  и
и  слились в одну точку. Выпустим из
слились в одну точку. Выпустим из  единичную нормаль
единичную нормаль  произвольным, по определенным образом. Раз направление
произвольным, по определенным образом. Раз направление  выбрано (среди двух возможных), то этим уже детерминировано определяется выбор
выбрано (среди двух возможных), то этим уже детерминировано определяется выбор  для всех точек
для всех точек  , если мы хотим, чтобы вектор
, если мы хотим, чтобы вектор  зависел от
зависел от  непрерывно. Однако в точке
непрерывно. Однако в точке  вектор
вектор 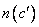 уже выбран, - ведь
уже выбран, - ведь  и
и  совпадают. Легко видеть, что если точку средней линии прямоугольника непрерывно двигать от
совпадают. Легко видеть, что если точку средней линии прямоугольника непрерывно двигать от  к
к  , то единичная нормаль
, то единичная нормаль  , где
, где  - точка листа Мёбиуса будет стремиться к -
- точка листа Мёбиуса будет стремиться к -  , а не к
, а не к  и, следовательно, вектор-функция
и, следовательно, вектор-функция  оказывается разрывной в точке
оказывается разрывной в точке  . Итак, лист Мёбиуса неориентируем.
. Итак, лист Мёбиуса неориентируем.

Поверзностный интеграл 2 рода.
Рассмотрим векторное поле  и поверхность S, которая описывается вектором
и поверхность S, которая описывается вектором

Предполагается, что функции x(u,v), y(u,v), z(u,v) являются непрерывно дифференцируемыми в некоторой области D(u,v), и что ранг матрицы

равен 2.
Обозначим через  единичный нормальный вектор к поверхности S в точке (x,y,z). Если поверхностьS гладкая и векторная функция
единичный нормальный вектор к поверхности S в точке (x,y,z). Если поверхностьS гладкая и векторная функция  непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора:
непрерывна, то в каждой точке поверхности существуют два противоположно направленных единичных нормальных вектора:

Выбор одного из них называется ориентацией поверхности.
Если S является границей ограниченной области, то ее можно ориентировать внешней или внутреннейнормалями. Поверхность S, ориентированную внешней нормалью, называют ее внешней стороной, а ориентированную внутренней нормалью, − ее внутренней стороной.
Поверхностный интеграл второго рода от векторного поля 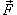 по ориентированной поверхности S (илипоток векторного поля
по ориентированной поверхности S (илипоток векторного поля 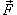 через поверхность S) может быть записан в одной из следующих форм:
через поверхность S) может быть записан в одной из следующих форм:
- Если поверхность S ориентирована внешней нормалью, то

- Если поверхность S ориентирована внутренней нормалью, то
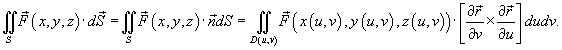
Величина 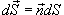 называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом:
называется векторным элементом поверхности. Точка обозначает скалярное произведение соответствующих векторов. Частные производные, входящие в последние формулы, вычисляются следующим образом:
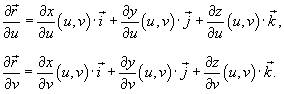
Если поверхность S задана явно в виде уравнения z = z(x,y), где z(x,y) − дифференцируемая функция в областиD(x,y), то поверхностный интеграл второго рода от векторного поля 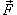 по поверхности S записывается в одной из следующих форм:
по поверхности S записывается в одной из следующих форм:
- Если поверхность S ориентирована внешней нормалью (k-компонент вектора нормали является положительным), то

- Если поверхность S ориентирована внутренней нормалью (k-компонент вектора нормали является отрицательным), то

Поверхностный интеграл второго рода можно записать также в координатной форме. Пусть P (x,y,z), Q (x,y,z),R (x,y,z) являются компонентами векторного поля 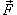 . Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали
. Введем cos α, cos β, cos γ − направляющие косинусы внешней нормали  к поверхности S. Тогда скалярное произведение
к поверхности S. Тогда скалярное произведение  равно
равно

Следовательно, поверхностный интеграл можно записать в виде

Поскольку  (рисунок 1), и, аналогично,
(рисунок 1), и, аналогично,  , получаем следующую формулу для вычисления поверхностного интеграла II рода:
, получаем следующую формулу для вычисления поверхностного интеграла II рода:

Если поверхность S задана в параметрической форме с помощью вектора  , то последняя формула принимает вид
, то последняя формула принимает вид

где (u,v) изменяются в пределах области интегрирования D(u,v).

| ||
| Рис.1 |
Если поверхность S не представима в явном или параметрическом виде, то ее можно попробовать разбить на конечное число частей, каждая из которых представима в таком виде. В этом случае справедливо свойство аддитивности: поверхностный интеграл второго рода по поверхности S будет равен сумме интегралов по ее частям.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...