
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Графы. Реализация графов на плоскости. Деревья.
Определение: Графом G (в широком понимании) называется любая пара (V,E), где V = {v1, v2, ... } - множество вершин графа, а E = {e1, e2, ... } – множество неориентированных ребер, причем допускаются пары вида (vi, vi) и одинаковые пары. Если пары в V рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным(орграфом).
Элементы множества V называются вершинами графа, а пары из E - его ребрами; в орграфе они называются ориентированными ребрами или дугами.
Говорят, что ребро e = (u,v) в неориентированном графе соединяет вершины u и v, а в ориентированном графе дуга e = (u,v) идет из вершины u в вершину v.
Пара вида (vi, vi) называется петлей в вершине vi(т.е. повторяются вершины в множестве). Если пара (vi, vj) встречается в E более одного раза, то говорят, что (vi, vj) - кратное ребро.
Определение: Говорят, что вершины vi и vj смежны в графе G = (V,E), если в E входит пара (vi, vj) или (vj, vi). Говорят, что ребро (дуга) (vi, vj) инцидентно вершинам vi и vj.
Определение: Смешанные графы - графы, в которых часть ребер ориентированы, а часть – нет.
Определение: Степенью вершины в неориентированном графе называется число ребер, инцидентных данной вершине, при этом петли учитываются дважды. Вершины степени 0 называют изолированными.
Определение: Путем в графе (орграфе) G = (V,E) называется последовательность вершин и ребер (дуг) вида v0, (v0, v1), v1, ... , vn-1, (vn-1, vn), vn, где все vi ℮ E и все (vi, vi+1) ℮ E. Длина пути - это число ребер (дуг) в нем. Говорят, что этот путь идет из v0 в vn.
Определение: Маршрутом в графе называют последовательность вершин, любая пара последовательности вершин в которой смежна.
Определение: Путь называется циклом, если vn = v0 и ребра (дуги) не повторяются(т.е. начальная и конечная вершины совпадают). Путь называется простым циклом, если vn = v0 и больше нет повторений вершин.
Определение: Граф G = (V,E) называется связным, если для любых двух вершин vi, vj О V в G существует путь из vi в vj.
Пара вершин называется связной, если существует маршрут, который их соединяет. Если в графе любая пара вершин связна, то граф называется связным.
Определение: Граф G = (V,E) называется деревом, если он связный и не содержит циклов. Вершины степени 1 в дереве называют его листьями.
Пусть задан неориентированный граф G = (V,E). Пусть каждой вершине vi из V сопоставлена точка ai в некотором евклидовом пространстве, причем ai ≠ aj при i ≠ j. Пусть каждому ребру e = (vi, vj) из E сопоставлена непрерывная кривая L, соединяющая точки ai и aj и не проходящая через другие точки ak. Тогда если все кривые, сопоставленные ребрам графа, не имеют общих точек, кроме концевых, то это множество точек и кривых называется геометрической реализацией графа G.
Теорема. Каждый конечный граф G можно реализовать в трехмерном евклидовом пространстве (без пересечения ребер).
Определение: Граф называется планарным, если существует его планарная реализация, то есть геометрическая реализация на плоскости (без пересечения ребер).
Определение:Связный граф называется Эйлеровым, если в нем присутствует цикл, содержащий все ребра.
Теорема. (формула Эйлера.) Для любой планарной реализации связного планарного графа G = (V,E) с p вершинами, q ребрами и r гранями выполняется равенство: p-q+r = 2.
Критерий Эйлера: граф является Эйлеровым т. и т. т., когда он связный и все степени его вершин четны.
№4.
Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
Правило суммы: пусть имеется n попарно непересекающихся множеств A1, A2, …, An , содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно m1 + m2 + … + mn.
Пример. Если на первой полке стоит X книг, а на второй Y, то выбрать книгу с первой или второй полки, можно X+Y способами.
Пример. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: По правилу суммы получаем 17+13=30 вариантов.
Кортеж - конечная последовательность (допускающая повторения) элементов какого-нибудь множества.
Правило произведения: пусть имеется n множеств A1, A2, …, An содержащих m1, m2, …, mn элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества, т. е. построить кортеж (а1, а2, ..., аn), где аi Î А i1 (i = 1, 2, …, n), равно m1 · m2 · … · mn.
Пример. Если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.
Пример. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение. Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
Выборки. Если из множества предметов выбирается некоторое подмножество, то его называют выборкой. Выборки бывают упорядоченные и неупорядоченные.
В упорядоченной выборке существенен порядок, в котором следуют ее элементы, другими словами, изменив порядок элементов, мы получим другую выборку.
Пример. Из цифр 1, 2, 3, 4, 5 можно составить следующие трехзначные числа 123, 431, 524, ...и т.д. Это упорядоченные трехэлементные выборки, так как 123 и 132 - разные числа.
Пример. Из 20 учащихся класса выбрать двух дежурных. Любая пара дежурных представляет собой неупорядоченную двухэлементную выборку, так как порядок их выбора не важен.
Размещения
Размещениями из n элементов по m элементов (m < n) называются комбинации, составленные из данных n элементов по m элементов, которые отличаются либо самими элементами, либо порядком элементов.
Число размещений без повторений из n по m (n различных элементов) вычисляется по формуле:

| (3.1) |
Размещениями с повторениями из n элементов по m называются упорядоченные m-элементные выборки, в которых элементы могут повторяться.
Число размещений с повторениями вычисляется по формуле:

| (3.2) |
Пример. Возьмем буквы Б, А, Р. Какие размещения из этих букв, взятых по две, можно получить? Сколько таких наборов получиться, если: 1) буквы в наборе не повторяются; 2) буквы могут повторяться?
Решение.
1. Получатся следующие наборы: БА, БР, АР, АБ, РБ, РА.
По формуле (3.1) получаем:  наборов.
наборов.
2. Получатся наборы: ББ, БА, БР, АА, АБ, АР, РР, РБ, РА.
По формуле (3.2) получаем:  наборов.
наборов.
Пример. Вдоль дороги стоят 6 светофоров. Сколько может быть различных комбинаций их сигналов, если каждый светофор имеет 3 состояния: "красный", "желтый", "зеленый"?
Решение. Выпишем несколько комбинаций: КККЖЗЗ, ЗЗЗЗЗЗ, КЖЗКЖЗ... Мы видим, что состав выборки меняется и порядок элементов существенен (ведь если, например, в выборке КЖЗКЖЗ поменять местами К и Ж, ситуация на дороге будет другой). Поэтому применяем формулу (3.2) и вычисляем число размещений с повторениями из 3 по 6, получаем  комбинаций.
комбинаций.
Перестановки
Перестановками из n элементов называются размещения из этих n элементов по n (Перестановки - частный случай размещений).
Число перестановок без повторений (n различных элементов) вычисляется по формуле:
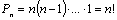
| (3.3) |
Число перестановок c повторениями (k различных элементов, где элементы могут повторяться m1, m2, …, mk раз и m1 + m2 +… + mk = n, где n - общее количество элементов) вычисляется по формуле:

| (3.4) |
Пример. Возьмем буквы Б, А, Р. Какие перестановки из этих букв можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) буква А повторяется два раза?
Решение.
1. Получатся наборы: БАР, БРА, АРБ, АБР, РАБ, РБА.
По формуле (3.3) получаем: 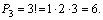 наборов.
наборов.
2. Получатся наборы: БАРА, БРАА, БААР, ААРБ, ААБР, АБАР, АРАБ, АРБА, АБРА, РАБА, РААБ, РБАА.
По формуле (3.4) получаем:  наборов.
наборов.
Пример. Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?
Решение. Из данных шести цифр можно составить Р6 = 6! = 720 перестановок. Но числа, начинающиеся на нуль, не являются шестизначными. Такие числа отличаются друг от друга перестановкой пяти остальных цифр, значит, их будет Р5 = 120. Поэтому шестизначных чисел будет 720 - 120 = 600 чисел.
Пример. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?
Решение. Первая линия шахматной доски представляет собой 8 клеток, на которых и надо расположить эти 8 фигур. Различные варианты расположения будут отличаться только порядком фигур, значит, это будут перестановки с повторениями Р8 (2,2,2).
По формуле (3.4) получаем:  способов.
способов.
Сочетания
Сочетаниями из n элементов по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (отличие сочетаний от размещений в том, что в сочетаниях не учитывается порядок элементов).
Число сочетаний без повторений (n различных элементов, взятых по m) вычисляется по формуле:

Число сочетаний c повторениями (n элементов, взятых по m, где элементы в наборе могут повторяться) вычисляется по формуле:

| (3.6) |
Пример. Возьмем буквы Б, А, Р. Какие сочетания из этих букв, взятых по две, можно получить? Сколько таких наборов получится, если: 1) буквы в наборе не повторяются; 2) можно брать по два одинаковые буквы.
Решение.
1. Получатся наборы: БА (БА и АБ - один и тот же набор), АР и РБ
По формуле (3.5) получаем:  наборов.
наборов.
2. Получатся наборы: ББ, БА, БР, АА, АР, РР.
По формуле (3.6) получаем:  наборов.
наборов.
Пример. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать?
Решение. Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов - это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.
По формуле (3.5) получаем:  способов.
способов.
Пример. В хлебном отделе имеются булки белого и черного хлеба. Сколькими способами можно купить 6 булок хлеба?
Решение. Обозначая булки белого и черного хлеба буквами Б и Ч, составим несколько выборок: ББББББ, ББЧЧББ, ЧЧЧЧЧБ, ... Состав меняется от выборки к выборке, порядок элементов несущественен, значит это - сочетания с повторениями из 2 по 6. По формуле (3.6) получаем  способов.
способов.
Cделаем проверку и выпишем все варианты покупки: ББББББ, БББББЧ, ББББЧЧ, БББЧЧЧ, ББЧЧЧЧ, БЧЧЧЧЧ, ЧЧЧЧЧЧ. Их действительно 7.
№5.
Вероятностное пространство.Свойства σ-алгебры и вероятности.Теорема о непрерывности вероятности.Примеры вероятостных пространств.
Определение1: Класс F - подмножествo Ω, то пара (Ω,F) называется σ-алгеброй, если F удовлетворяет условиям:
1. ΩϵF ;
2. Если AϵF, то 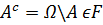
3. Если 
Если F-σ-алгебра подможетв пространства Ω, то пара (Ω,F) называется измеримым пространством.
Определение 2: Пусть (Ω,F) – измеримое пространство. Функция множеств Р(.): F->[0;1], удовлетворяющая условиям:
1. Р(Ω)= 1.
2.если (  ϵ F,
ϵ F,  ∩
∩ 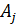 , при i ≠j, то Р(
, при i ≠j, то Р(  )=
)= 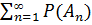 – называется вероятностью.
– называется вероятностью.
При этом (Ω,F,P(.)) называется вероятностным пространством, а свойства 1 и 2 – аксиомами вероятностного пространства, Ω – называется пространством элементарных событий, элементы σ-алгебры F называются случайными событиями.
Теорема о непрерывности вероятности:
Пусть (Ω,F,P)- вероятностное пространство. Тогда:
1. Если  ϵ F ,
ϵ F ,  , nϵN, то
, nϵN, то  )
)
2. Если  ϵ F ,
ϵ F ,  , nϵN, то
, nϵN, то  )
)
6 Условная вероятность. Независимость
Определение 6.1. Условной вероятностью случайного события А относительно случайного события B , имеющего ненулевую вероятность, называется
P(A|B) = 
Теорема 6.1. (Формула полной вероятности). Пусть А - случайное событие; J - конечное или счетное множество; (  ) - семейство случайных событий, удовлетворяющее
) - семейство случайных событий, удовлетворяющее
условиям: P (  ) ≠ 0 для каждого jϵJ,
) ≠ 0 для каждого jϵJ,  ∩
∩  = Ø при i ≠ j, А⊂
= Ø при i ≠ j, А⊂ 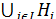 . Тогда
. Тогда
P (А) = 
Теорема 6.2. (Формула Байеса). Пусть выполнены условия теоремы 5.1. и P(А)≠0. Тогда

Определение 6.2. События А и B называются независимыми, если
P(А∩B) =P(A)P(B).
Определение 5.3. События A1,...,An называются независимыми в совокупности, если
P(  ∩…
∩… 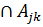 )=P(
)=P(  P(
P( 
для любого k, 1<k≤n, и для любых j1, … ,  таких, что 1
таких, что 1 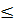 j1 < … <
j1 < … <  ≤ n.
≤ n.
События А1, А2, … называются независимыми в совокупности, если для любого n > 1 события А1, …, Аn независимы в совокупности.
Утверждение 5.3. Пусть А1, … , Аn - независимые в совокупности события, Bj = Aj либо Bj = 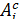 , j = 1, … , n. Тогда B1, … , Bn - независимые в совокупности события.
, j = 1, … , n. Тогда B1, … , Bn - независимые в совокупности события.
Вопрос № 37.
Случайная величина. Функция распределения случайной величины. Плотность распределения. Примеры вероятностных пространств и случайных величин.
Определение: Пусть (W, f) и (Х, В) - два измеримых пространства. Функция x(·): W®Х (с областью определения W и множеством значений в Х) называется f |В - измеримой, если
x-1(В) = {w | x(w)ÎВ}Îf " ВÎВ.
Определение: Пусть (W, f, P) - вероятностное пространство и (Х, В) - некоторое измеримое пространство. f |В - измеримая функция x: W®Х называется случайным элементом.
В частном случае, когда X=R1, B= B(R1) функцию x называют случайной величиной.
Если X = Rn, B = B(Rn) функцию x называют случайной вектором.
Пусть (W, f, P) - вероятностное пространство. Пусть x - случайная величина, определённая на этом пространстве.
Определение:
1) Fx(x) = P{x £ x}, xÎR называется функцией распределения случайной величины x.
2) Qx(B) = P{xÎ B}, BÎB(R ) называется распределением случайной величины x.
3) Если существует борелевская функция fx(x): P{xÎ B}=  , " BÎB(R ), то fx(x) называется плотностью распределения случайной величины x.
, " BÎB(R ), то fx(x) называется плотностью распределения случайной величины x.
4) Если множеством значений случайной величины x является не более чем счётное
{x1, …}Ì R, то говорят, что x - дискретная случайная величина, а набор вероятностей р(к) = Р{x = хк} к = 1, 2, …называется распределением дискретной случайной величины:
р(к) ³ 0 и  рк =
рк =  Р{x = хк}= (в силу аддитивности) = Р(
Р{x = хк}= (в силу аддитивности) = Р(  {x = хк}) = Р(W) = 1.
{x = хк}) = Р(W) = 1.
Свойства функции распределения:
1) Если -¥ < a < b < +¥ |Þ Fx(a) £ Fx(b). P{a < x £ b}= Fx(b) - Fx(a).
Доказательство:
Рассмотрим {x £ a}, {x £ b} {x £ a}Ì{x £ b}, {a < x £ b}={x £ b}\{x £ a}.
2) 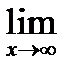 Fx(x) = 1,
Fx(x) = 1,  Fx(x) = 0.
Fx(x) = 0.
Доказательство:
В силу монотонности Fx достаточно показать, что  Fx(n) = 1,
Fx(n) = 1,  Fx(-n) = 0.
Fx(-n) = 0.
10 Рассмотрим события {x £ n}Ì{x £ n+1}- последовательность монотонно возрастает |Þ
 {x £ n}=
{x £ n}=  {x £ n} = {x < ¥} Р{|x| = ¥}= 0.
{x £ n} = {x < ¥} Р{|x| = ¥}= 0.
 Fx(n) =
Fx(n) =  Р{x £ n}= Р{x < ¥}= 1.
Р{x £ n}= Р{x < ¥}= 1.
20 {x £ -n}É{x £ -(n+1)}- монотонно убывает |Þ  {x £ -n}=
{x £ -n}=  {x £ -n} = {x = -¥}
{x £ -n} = {x = -¥}
 Fx(-n) =
Fx(-n) =  Р{x £ -n}= Р{x = -¥}= 0. (что и требовалось доказать)
Р{x £ -n}= Р{x = -¥}= 0. (что и требовалось доказать)
3) Функция Fx(x) непрерывна справа в каждой точке, т.е. если x < xn+1 < xn;  xn = x, то
xn = x, то
 Fx(xn) = Fx(x).
Fx(xn) = Fx(x).
Доказательство:
Рассмотрим {x £ xn}É{x £ xn+1}- последовательность событий |Þ последовательность монотонно убывает и  {x £ xn}=
{x £ xn}=  {x £ xn}= {x £ x}.
{x £ xn}= {x £ x}.
 Fx(xn) =
Fx(xn) =  Р{x £ xn}= P{x £ x}.
Р{x £ xn}= P{x £ x}.
4)  Fx(y) = P{x < x}.
Fx(y) = P{x < x}.
Надо доказать, что если xn < xn+1 < x и  xn = x, то
xn = x, то  Fx(xn) = P{x < x}.
Fx(xn) = P{x < x}.
Доказательство:
{x £ xn}Ì{x £ xn+1}.
 {x £ xn}=
{x £ xn}=  {x £ xn} = {x < x}.
{x £ xn} = {x < x}.
 Fx(xn) =
Fx(xn) =  Р{x £ xn}= (по теоремы о непрерывности меры) = Р{x < x}.
Р{x £ xn}= (по теоремы о непрерывности меры) = Р{x < x}.
 {x £ xn}= {x £ x}
{x £ xn}= {x £ x}  {x £ xn} = {x £ x}
{x £ xn} = {x £ x}
] ] ] ] ] |
x xn xn ® x
5) P{x = x} = Fx(x) - Fx(x-).
Доказательство: {x = x}={x £ x}\{x < x}. Значит Р{x = x}=Р{x £ x}- Р{x < x}.
6) Пусть x - дискретная случайная величина принимающая значения {x1, x2, …} с вероятностями {р(1), р(2), …}.
Fx(x) = P{x £ x}= P({x £ x}ÇW) = (где W =  {x = хк}) = Р(
{x = хк}) = Р(  {x £ x, x = хк}) =
{x £ x, x = хк}) =
=  Р{x £ x, x = хк}=
Р{x £ x, x = хк}=  P(k).
P(k).
Определение: Функция F(x), xÎR называется функцией распределения, если она обладает свойствами:
1) F(x) монотонно не убывает,
2) F(x) непрерывна справа,
3)  F(x) = 1,
F(x) = 1,  F(x) = 0.
F(x) = 0.
Теорема: 1) Если Q - распределение на (R, B(R )), то F(x) = Q(]-¥, x]) является функцией распределения, xÎR.
2) Если F(x) - функция распределения, то $ распределение Q на (R, B(R )): F(x) = Q(]-¥, x])
" xÎR.
Доказательство:
1) а) a < b Þ Q(]-¥, a]) £ Q(]-¥, b]) в силу монотонности меры.
b) если x < xn+1 < xn : lim xn = x, то  Q(]-¥, xn]) = Q(]-¥, x]).
Q(]-¥, xn]) = Q(]-¥, x]).
c)  Q(]-¥, n]) = Q(R) = 1,
Q(]-¥, n]) = Q(R) = 1,  Q(]-¥, -n]) = Q(Æ) = 0.
Q(]-¥, -n]) = Q(Æ) = 0.
2) Если F(x) - функция распределения Þ $! Q(·) на (R, B(R )): Q(]a, b]) = F(b) - F(a).
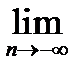 Q(]a, b]) = Q(]-¥, b]) = F(b).
Q(]a, b]) = Q(]-¥, b]) = F(b).
Q(R ) =  Q(]-¥, b]) = 1. (что и требовалось доказать)
Q(]-¥, b]) = 1. (что и требовалось доказать)
Следствие 1: Пусть F - функция распределения. Тогда $ (W, f, P) - вероятностное пространство и x определённая на этом пространстве: F(x) = P{x £ x}.
Доказательство:
Положим W = R, f = B(R ), P - распределение соответствующее F. Определим
x(w): x(w) = w. P{x £ x} = P{w: x(w) £ x} = P(]-¥, x]) = F(x).
Определение.Cлучайная величина ξ имеет абсолютно непрерывное распределение, если существует неотрицательная функция  такая, что для любого борелевского множества B имеет место равенство:
такая, что для любого борелевского множества B имеет место равенство:
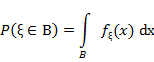
Функцию  называют плотностью распределения случайной величины ξ .
называют плотностью распределения случайной величины ξ .
Замечание.Интеграл выше есть интеграл Лебега. При этом площадь над множеством B, имеющим нулевую меру Лебега, равна нулю. Заметим, что любая функция, отличающаяся от функции  лишь в конечном или счётном числе точек (или на множестве нулевой меры Лебега), будет являться плотностью того же распределения, так как интеграл не изменится от изменения подынтегральной функции на множестве меры нуль.
лишь в конечном или счётном числе точек (или на множестве нулевой меры Лебега), будет являться плотностью того же распределения, так как интеграл не изменится от изменения подынтегральной функции на множестве меры нуль.
Теорема.Плотность распределения обладает свойствами:
(f1)  для любого x; (f2)
для любого x; (f2) 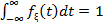 .
.
Доказательство. (f1) выполнено по определению плотности, (f2) также следует из определения:

QED
Эти два свойства полностью характеризуют класс плотностей:
Теорема .Если функция f обладает свойствами (f1) и (f2), то существует вероятностное пространство и случайная величина ξ на нём, для которой f является плотностью распределения.
Доказательство.Пусть Ω есть область, заключенная между осью абсцисс и графиком функции f. Площадь области Ω равна единице по свойству (f2). Пусть F — множество борелевских подмножеств Ω, а P — мера Лебега (площадь) на множествах из F. И пусть случайная величина ξ есть абсцисса точки, наудачу брошенной в эту область.

Тогда для любого  выполнено:
выполнено:

| (10) |
Здесь область  есть криволинейная трапеция под графиком плотности, с основанием B. По определению, равенство (10) означает, что функция f является плотностью распределения случайной величины ξ
есть криволинейная трапеция под графиком плотности, с основанием B. По определению, равенство (10) означает, что функция f является плотностью распределения случайной величины ξ
QED
Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-либо грани в данном случае в теории вероятностей называется элементарным событием  [1], то есть
[1], то есть
· 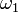 — грань с одной точкой;
— грань с одной точкой;
·  — грань с двумя точками;
— грань с двумя точками;
· ...
·  — грань с шестью точками.
— грань с шестью точками.
Множество всех граней  образует пространство элементарных событий
образует пространство элементарных событий  , подмножества которого называются случайными событиями
, подмножества которого называются случайными событиями 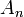 [1]. В случае однократного подбрасывания игровой кости примерами событий являются
[1]. В случае однократного подбрасывания игровой кости примерами событий являются
· выпадение грани с нечётным количеством точек, то есть событие  — это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие
— это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие  записывается как множество, содержащее элементарные события:
записывается как множество, содержащее элементарные события: 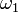 ,
,  и
и  . Таким образом,
. Таким образом,  ;
;
· выпадение грани с чётным количеством точек, то есть событие  — это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие
— это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие  записывается как множество, содержащее элементарные события:
записывается как множество, содержащее элементарные события:  ,
,  и
и  . Таким образом,
. Таким образом,  ;
;
Вопрос 38
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...