Оценка погрешности интерполяции.

Погрешность интерполяции (остаточный член) : . В узлах интерполирования он равен 0. В других точках он вообще-то не известен, если не известна функция f(x). Но его можно оценить, если f(x) достаточно гладкая функция.

Пусть – произвольная, несовпадающая с узлом, точка, зафиксируем ее и рассмотрим функцию от переменной s:

Она обращается в нуль при -всего в (n+2)-ух точках. По теореме Ролля между двумя корнями гладкой функции есть корень производной => функция имеет по крайней мере (n+1) корней. То есть, => дифференцируя формулу (Gs) (n+1) раз по s , получим, что в этой точке выполняется

Итого, мы получили, что для любой точки существует ( зависит от x) такая, что

Формула (1) называется формулой погрешности интерполяции. От можно избавиться, если взять максимум производной, тогда получим оценку погрешности интерполяции:

Отсюда видно, что погрешность зависит от самой функции (от 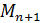), от количества точек интерполяции (от n) и от их расположения (от ). Если производные у функции равномерно ограничены 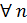(например, ), то с ростом n погрешность интерполяции будет быстро стремиться к нулю.

14. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Способы конструирования квадратурных формул

Рассмотрим простейшие, но широко используемые в практических вычислениях формулы: прямоугольников (с центральной точкой), трапеций, Симпсона. Способ их получения состоит в следующем. Разобьем отрезок интегрирования [a,b] на N частей точками .

Положим, что так что

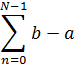
В дальнейшем будем называть – узлами, — шагами интегрирования. Иногда отрезок от до будем именовать элементарным отрезком. В частном случае шаг интегрирования может быть постоянным: . Также будем использовать обозначение .

После введения шагов интегрирования искомый интеграл можно представить в виде

где

14.2 Формула прямоугольников

Считая малым параметром, заменим в (3.1) площадью прямоугольника с основанием и высотой _. Тогда придем к локальной формуле прямоугольников

Суммируя в соответствии с (3.1) приближенные значения по всем элементарным отрезкам, получаем формулу прямоугольников для вычисления приближения к I:

В частном случае, когда формула прямоугольников принимает вид

Можно конструировать аналогичные формулы, используя в качестве высоты элементарных прямоугольников значениеf(x) не в середине отрезка, а на границе (левой или правой). Но в этом случае существенно ухудшается точность приближения вычисляемого интеграла.

Формула трапеций

На элементарном отрезке 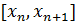заменим подынтегральную функцию интерполяционным полиномом первой степени:

Выполняя интегрирование на отрезке, приходим к локальной формуле трапеций:

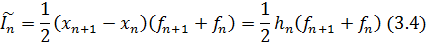
Замечание. Название формулы связано с тем, что интеграл по элементарному отрезку заменяется площадью трапеции с основаниями, равными значениям f(x) на краях отрезка, и высотой, равной _.

Суммируя (3.4) по всем отрезкам, получаем формулу трапеций для вычисления приближения к I:

В случае постоянного шага интегрирования формула принимает вид:

14.4 Формула Симпсона

На элементарном отрезке 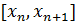используя значение функции в центре отрезка, заменим подынтегральную функцию f(x) интерполяционным полиномом второй степени:

Напомним, что мы обозначили: а значение в полуцелой точке

Вычисляя интеграл от полинома на отрезке 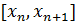приходим к локальной формуле Симпсона:

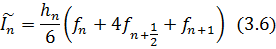
Суммируя (3.6) по всем отрезкам, получаем формулу Симпсона для вычисления приближения к I:

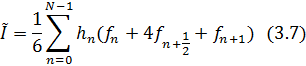
Для постоянного шага интегрирования
формула Симпсона принимает вид

Замечание. Последнюю формулу иногда записывают без использования дробных индексов, в виде

К этой записи приходим, если под локальной формулой понимать результат интегрирования по паре элементарных отрезков:

где — интерполяционный полином второй степени для f(x) на построенный по значениям в точках . Суммируя локальные приближения по всем парам, получим (3.8а). Разумеется, число пар на [a, b] в этом случае должно быть целым, т. е. N — четным.

Формулы, используемые для приближенного вычисления интеграла, называются квадратурными.