Понятие первообразной функции на промежутке. Понятие неопределенного интеграла.

Понятие первообразной функции на промежутке. Понятие неопределенного интеграла.

Пусть

О называется первообразной функции на ,

если первообразная дифференцируема на этом интервале

и выполняется равенство ,

О Пусть функция определенна на некотором промежутке. Множество всех первообразных функции на этом промежутке называется неопределенным интегралом. , где – подынтегральная функция.

Таблица неопределенных интегралов основных элементарных функций.

1.

2.

3.

4.

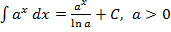
5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Понятия разбиения, диаметра разбиения, интегральных сумм и определенного интеграла.

О
Разобьем отрезок точками так, чтобы

Говорят, что задано разбиение отрезка .

Обозначим через , ,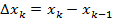

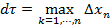
называется диаметром разбиения .

Выберем на каждом отрезке разбиения произвольным образом точку .

Составим сумму:

— интегральная сумма функции ,

составленная по разбиению и точек .

О Если существует число такое, что для можно найти так, что для любого разбиения 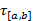c и при любом выборе точек выполняется , то число называется определенным интегралом функции по отрезку , а функция называется интегрируемой по Риману на этом отрезке.

– нижний предел интегрирования, – верхний, – подынтегральная функция.

Таким образом, определенный интеграл

Геометрический смысл определенного интеграла: понятие криволинейной трапеции, вычисление ее площади.

Возьмем произвольное разбиение

на отрезке разбиения

где

Рассмотрим произведение

– площадь k-ого прямоугольника, построенного на k-ом отрезке разбиения и высотой

Тогда

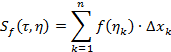
– сумма площадей всех получившихся прямоугольников.

Т. к. при уменьшении диаметра разбиения сумма площадей прямоугольников приближается к площади криволинейной трапеции, а сами интегральные суммы стремятся к . Геометрический смысл определенного интеграла – это площадь криволинейной трапеции на отрезке .

Классы интегрируемых функций.

1. Если функция монотонна, то она интегрируема по Риману на .

2. Для того чтобы функция была интегрируема по Риману на , достаточно, чтобы она была непрерывной.

3. Если функция непрерывна на , за исключением конечного числа точек разрыва 1-го рода (такая функция называется кусочно-непрерывной), то она интегрируема по Риману на .

Определение интеграла с переменным верхним пределом.

Пусть интегрируема по Риману на . Тогда функция интегрируема по Риману на 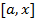, и, значит, определена функция:

– эта функция называется интегралом с переменным верхним пределом (ИСПВП).

Площадь области в декартовой системе координат.

Рассмотрим криволинейную трапецию, ограниченную сверху , снизу и прямыми , , где и непрерывны на .

Длина кривой в декартовой системе координат.

Пусть непрерывна и дифференцируема на .

Тогда длина кривой , вычисляется по формуле:

Объем тела вращения.

Рассмотрим криволинейную трапецию. на .

Найдем объем тела, полученного вращением вокруг оси Ох:

Аналогично вычисляется объем тела, полученного вращением вокруг оси Oу:

Несобственные интегралы 1-го рода (интегралы с бесконечными пределами интегрирования), их сходимость, расходимость.

Пусть , причем интегрируема по Риману на .

Символ 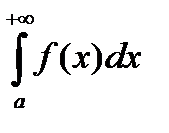называется несобственным интегралом (Н. И.) 1-го рода.

Н. И. 1-ого рода называется сходящимся, если существует и конечен, причем считается равным этому пределу. В противном случае Н. И.1-ого рода называется расходящимся, т.е., когда предел не существует или равен бесконечности.

Аналогично вводится понятие Н. И. для .

Можно также рассмотреть Н. И. вида , где определена на .

Этот Н. И. 1-го рода сходится в том случае,

когда сходятся оба интеграла и .

Н. И. 1-ого рода расходится, если хотя бы один из них расходится.

Двойные интегралы.

Пусть – компакт в

Разобьем область произвольным образом на ячейки – разбиение области . Обозначим – площадь ячейки , а

– диаметр разбиения . Возьмем в каждой ячейке произвольную точку

Составим интегральную сумму:

О Число называется двойным интегралом функции по множеству ,

если существует такое, что для любого разбиения , у которого ,

при любом выборе точек выполняется неравенство .

Двойной интеграл обозначается символом

Теорема Фубини.

Пусть 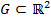такова, что ,

где и – функции, непрерывные на .

Если интегрируема на , причем функция интегрируема на , то двойной интеграл сводится к повторному интегралу по формуле:

Физическая задача

Скорость движения материальной точки задается законом .

Требуется найти закон передвижения точки .

Используя физический смысл производной:

Предположим, что

Ответ:

Геометрическая задача

Найдите семейство всех кривых, для которых угловой коэффициент касательной равен ординате точки касания.

Предположим, что искомая кривая

Фиксируем

Используя физический смысл производной:

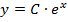( тоже входит в решение)

Задача о народонаселении

В 2012 году население Земли составило 7 миллиардов жителей.

Какого будет население Земли в 2022 году, если темп роста населения – величина постоянная ( ).

Пусть – число жителей Земли в момент времени .

Считаем:

Темп роста населения:

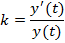
Найдем миллиардов.

ДУ:

Экономическая задача

Если задана эластичность спроса , то можно найти функцию спроса.

А именно, если – цена, то – функция спроса.

ДУ имеет вид:

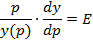
Метод решения ДУ с РП

Уравнение сводим к виду и

если 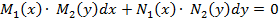, ДУ с РП, то разделяем обе переменные в разные стороны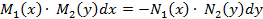

и интегрируем обе части

В результате интегрирования появляется константа,

которую можно записать в любой части ДУ.

Понятие первообразной функции на промежутке. Понятие неопределенного интеграла.

Пусть

О называется первообразной функции на ,

если первообразная дифференцируема на этом интервале

и выполняется равенство ,

О Пусть функция определенна на некотором промежутке. Множество всех первообразных функции на этом промежутке называется неопределенным интегралом. , где – подынтегральная функция.

Таблица неопределенных интегралов основных элементарных функций.

1.

2.

3.

4.

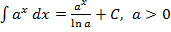
5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.