Capacity of two-wire transmission lines.

Capacity of two-wire transmission lines.

The capacity of two-wire symmetric circuits is similar to the capacitor capacity in which role of plates is carried out by wires. There are working capacity which is formed by two wires, of one (considered) circuit, and partial capacities, between a wire "a" of considered circuit and wires of other (neighboring) circuits, and between a wire "b" and wires of other circuits, and also partial capacities between each wire of a considered circuit and the ground. The main capacity which characterizing transfer (transfer parameter) is the working capacity. It is known, that the capacity represents the relation of charge Q on a wire circuit, to a potential difference between them

. (2.84)

Let's assume that the charge is distributed on conductor’s surfaces that correspond to the reality and interaction between wires is absent since they are located widely spaced. From electrodynamics course it is known, that the potential difference between two points which are on distance L from each other is defined by a ratio

, (2.85)

where 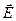- a vector of electric fieldintensity;

- a length vector element of a way between wires according to fig. 2.10 equal 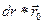, where 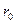- unit vector directed by L line.

Then

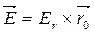, (2.86)

since vector 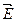of a two-wire circuit ТЕМ wave has only one component(fig. 2.2).

Thus scalar product under the sign of integral in (2.85) is defined by ratio .

According to Coulomb’s law intensity of the electric field created by charge Q on distance r from it, is defined by a ratio

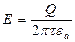, (2.87)

where 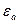- absolute dielectric permeability of medium.

If we locate cylindrical system of coordinates in the centre of wire 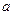then intensity of the field created by a charge of this wire 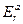on distance r from it will be defined by expression:

, (2.88)

Intensity of a field from a charge on wire 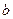, 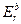in the same point will be equal

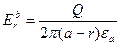, (2.89)

where 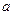- distance between wires.

The resultant intensity of a field on distance r from the beginning of coordinates will be equal

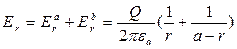. (2.90)

Then the potential difference between wires U is defined by a ratio:

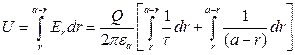. (2.91)

After integration and substitution of integration limits we will receive

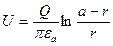. (2.92)

The capacity of a two-wire circuit will be defined by expression

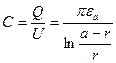. (2.93)

Absolute dielectric permeability

,

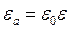where 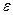- relative dielectric permeability of dielectric in space between wires;

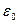- an electric constant equal in SI F/m = F/km.

Taking into account value of 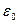, we will receive for the two-wire circuit located in free space (far from the ground), the formula defining working capacity

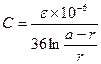, F/km (2.94)

where 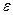- relative dielectric permeability of insulation between wires. In absence of dielectric the space between wires occupies air, for which .

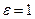Real constructions of symmetric cables, as a rule, contain many pairs and are in the general metal covers. Taking into account closeness of the adjacent pairs and influence of an external metal cover, capacity of symmetric cables for various types of twisting can be calculated by the following formula, F/km:

, (2.127)

where 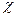- twisting coefficient of cable circuits (1,02—1,07); 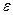- effective dielectric permeability of isolation;

- correction coefficient, that characterises closeness of conductors’ metal cover.

Calculation formulas of coefficient for various kinds of cables groups are resulted below:

Twisting type Correction coefficient

Pair . . . .

Star. . . .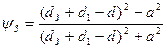

Double pair.

Capacity of two-wire transmission lines.

The capacity of two-wire symmetric circuits is similar to the capacitor capacity in which role of plates is carried out by wires. There are working capacity which is formed by two wires, of one (considered) circuit, and partial capacities, between a wire "a" of considered circuit and wires of other (neighboring) circuits, and between a wire "b" and wires of other circuits, and also partial capacities between each wire of a considered circuit and the ground. The main capacity which characterizing transfer (transfer parameter) is the working capacity. It is known, that the capacity represents the relation of charge Q on a wire circuit, to a potential difference between them

. (2.84)

Let's assume that the charge is distributed on conductor’s surfaces that correspond to the reality and interaction between wires is absent since they are located widely spaced. From electrodynamics course it is known, that the potential difference between two points which are on distance L from each other is defined by a ratio

, (2.85)

where 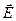- a vector of electric fieldintensity;

- a length vector element of a way between wires according to fig. 2.10 equal 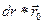, where 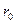- unit vector directed by L line.

Then

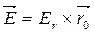, (2.86)

since vector 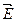of a two-wire circuit ТЕМ wave has only one component(fig. 2.2).

Thus scalar product under the sign of integral in (2.85) is defined by ratio .

According to Coulomb’s law intensity of the electric field created by charge Q on distance r from it, is defined by a ratio

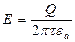, (2.87)

where 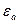- absolute dielectric permeability of medium.

If we locate cylindrical system of coordinates in the centre of wire 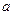then intensity of the field created by a charge of this wire 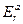on distance r from it will be defined by expression:

, (2.88)

Intensity of a field from a charge on wire 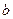, 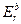in the same point will be equal

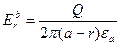, (2.89)

where 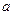- distance between wires.

The resultant intensity of a field on distance r from the beginning of coordinates will be equal

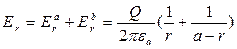. (2.90)

Then the potential difference between wires U is defined by a ratio:

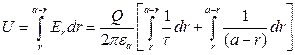. (2.91)

After integration and substitution of integration limits we will receive

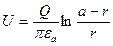. (2.92)

The capacity of a two-wire circuit will be defined by expression

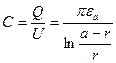. (2.93)

Absolute dielectric permeability

,

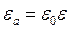where 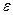- relative dielectric permeability of dielectric in space between wires;

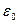- an electric constant equal in SI F/m = F/km.

Taking into account value of 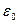, we will receive for the two-wire circuit located in free space (far from the ground), the formula defining working capacity

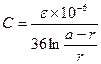, F/km (2.94)

where 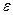- relative dielectric permeability of insulation between wires. In absence of dielectric the space between wires occupies air, for which .

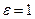Real constructions of symmetric cables, as a rule, contain many pairs and are in the general metal covers. Taking into account closeness of the adjacent pairs and influence of an external metal cover, capacity of symmetric cables for various types of twisting can be calculated by the following formula, F/km:

, (2.127)

where 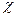- twisting coefficient of cable circuits (1,02—1,07); 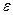- effective dielectric permeability of isolation;

- correction coefficient, that characterises closeness of conductors’ metal cover.

Calculation formulas of coefficient for various kinds of cables groups are resulted below:

Twisting type Correction coefficient

Pair . . . .

Star. . . .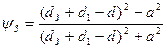

Double pair.