Стратегии инвестирования на финансовых рынках

Стратегии инвестирования на финансовых рынках

Семенихин А.И.

Введение и обзор

Инструменты инвестирования в современном мире – это, в основном, те или иные ценные бумаги. Чтобы показать объемы инвестирования приведем следующие цифры (данные 2006 года):

- ежедневный оборот на межбанковской валютной бирже Forex – 4 трлн. долл. (в год более 1200 трлн. долл.);

ежедневный объем мирового рынка ценных бумаг – около 300 млрд. долл. (в год более 90 трлн. долл.)

Для сравнения заметим, что мировой экспорт товаров за весь 2006 год составил 11,76 трлн. долл, а экспорт услуг - 2,71 трлн. долл.[1]

Применение вероятностного подхода к анализу движения цен фондового рынка ведет свою историю с диссертации француза Луи Башелье, опубликованной в 1900. Луи Башелье (Lui Bachelier, 1870-1946 г.г.) предложил рассматривать движение фондовых цен как «случайное блуждание». Приращения фондовых цен по его оценкам имели нормальное распределение.[2]

Работа Л. Башелье была недооценена современниками, практически забыта вплоть до своего повторного опубликования в 1964 году[3] в сборнике работ, посвященных вероятностным исследованиям фондового рынка. Сегодня Л. Башелье считается основателем финансовой математики.

В 60-70-х годах XX века идеи Л. Башелье получили развитие в работах П. Самуэльсона (Pall A. Samuelson), в моделях оценки опционов, предложенных Робертом Мертоном (Robert C. Merton) и Фишером Блэком (Fischer Black) вместе с Мироном Шоулзом (Myron Scholes).

Следующей революционной работой следует назвать статью Гарри Марковица (Harry Markowitz) «Выбор портфеля», опубликованную в 1952 году.[4] В последующие годы модель Г. Марковица получила развитие в работах Джеймса Тобина (James Tobin) и Уильяма Шарпа (William F. Sharpe).

Модель Марковица

Приведем самые общие допущения портфельного анализа, касающиеся индивидуального инвестора, определяющие степень знания инвестора о рынке и некоторые свойства рынка

1. Не существует операционных издержек или налогов, связанных с покупкой или продажей ценных бумаг.

2. Все инвестиционные решения принимаются только на один период времени.

3. Инвесторы могут прогнозировать ожидаемую величину доходности каждой ценной бумаги.

4. Инвесторы могут прогнозировать среднеквадратическое отклонение распределения вероятностей доходности каждой ценной бумаги. Когда каждая ценная бумага рассматривается отдельно, они используют эту цифру так, как будто она является полным измерением риска. Они могут предсказать корреляцию между доходностями для любой пары ценных бумаг.

5. Привлекательность ценной бумаги или портфеля полностью определяется тремя переменными: а) ожидаемой доходностью; б) индивидуальным риском, измеренным среднеквадратическим отклонением (или дисперсией) доходности и корреляцией данных с доходностью других ценных бумаг или их портфелем.

По поводу допущений Бромвич М. разумно замечает[9] : В теории инвестиционного портфеля считается, что инвесторы не осуществляют такие расчеты для получения ожидаемого дохода от ценных бумаг. Скорее в теории предполагается, что инвесторы действуют таким образом, как будто их «наилучшее мнение» относительно доходности любых ценных бумаг эквивалентно теоретической ожидаемой доходности. Это очень важное замечание, которое может быть отнесено, вообще, к взаимосвязи экономической теории и практики.

Логика дальнейшего изложения модели Марковица такова (конкретные выкладки осуществляются для портфеля из двух ценных бумаг):

1. Вводится и исследуется функция полезности инвестора от доходности и риска ценных бумаг.

2. На основе функции полезности строятся кривые безразличия доходности и риска для каждого уровня полезности.

3. Выводятся формулы доходности и риска портфеля ценных бумаг в зависимости от структуры портфеля и известных доходности и риске каждой ценной бумаги.

4. Строится допустимое и эффективное множества доходов и рисков портфелей ценных бумаг различной структуры при известных доходах и рисках каждой ценной бумаги.

5. На эффективном множестве находится точка касания кривых безразличия и эффективного множества – оптимальная точка для каждого инвестора.

Рис 1. Поведение инвестора не склонного к риску

Теперь покажем функцию полезности для инвестора, который, скорее всего, будет участвовать в азартной игре. Теперь наш игрок является оптимистом и оценивает вероятный выигрыш выше столь же вероятной потери. Он готов даже заплатить за участие в такой игре сумму, определяемую точкой F.[10] Величина платы так же определяется точкой, делящей пополам отрезок от точки полезности выигрыша до точки вреда проигрыша.

Рис 2. Поведение азартного инвестора

В теории инвестиционного портфеля предполагается, что игрок избегает риска, во всяком случае, ожидает за дополнительный риск дополнительный доход.

Если выражаться точнее, то в теории инвестиционного портфеля принимают разумные допущения относительно предпочтений между риском и доходностью ценной бумаги:

1. Предполагается, что при прочих равных условиях инвесторы предпочитают большую доходность меньшей.

2. Инвесторы предпочитают меньший риск большему, т. е. предполагается, что инвесторы избегают риска.

Отсюда правило:

Инвестор будет максимизировать свой ожидаемый доход при данной степени риска или минимизировать свой риск при данном уровне дохода.

В геометрической трактовке модели Марковица используются так называемые кривые безразличия. Кривые безразличия показывают зависимость доходности и риска при постоянных уровнях полезности и строятся из функции полезности, связывающей полезность с доходностью и риском.

В теории инвестиционного портфеля обычно предполагается, что предпочтения инвесторов описываются квадратной функцией полезности.[11]

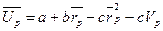, где

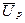- ожидаемая полезность портфеля;

- ожидаемая доходность портфеля;

- дисперсия (волатильность) доходности портфеля.

Такая функция соответствует нашим допущениям относительно поведения инвесторов. Рост ожидаемой доходности ведет к росту полезности. Рост риска, наоборот, уменьшает полезность. Два отрицательных члена в правой части уравнения обеспечивают постепенное замедление роста полезности по мере увеличения доходности.

При графическом представлении часто связывают доходность в процентах и среднеквадратическое отклонение. Дело в том, что размерность дисперсии (волатильности) – это квадрат процентов. Среднеквадратическое отклонение – корень квадратный из дисперсии – дает размерность сопоставимую с доходностью. Впрочем, графическое представление при этой замене меняется не существенно.

Квадратная форма функции полезности для инвестора, избегающего некомпенсируемого риска, дает кривую безразличия близкую к следующей

Рис. 3. Кривые безразличия

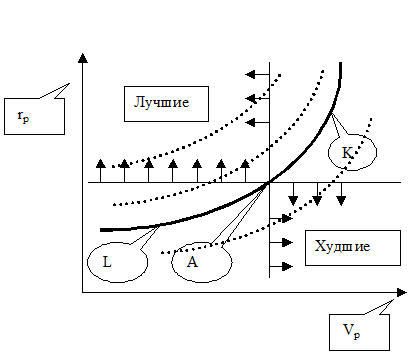
Риск инвестиционного портфеля

Если портфель состоит из двух ценных бумаг ( и ), а весами являются их доли ( и ) в портфеле, тогда из основного определения дисперсии (волатильности) пишем:

.

Путем простых преобразований приходим к следующему (подробный вывод см. в Приложении к модели Г. Марковица):

или

,

где

- коэффициент корреляции доходностей двух ценных бумаг

- среднеквадратические отклонения распределения доходностей двух ценных бумаг

Если учесть, что дисперсия есть частный случай ковариации случайной величины с самой собой, то выведенная формула может быть распространена на измерение риска портфеля из любого количества ценных бумаг:

Напомним формулы коэффициента корреляция и ковариации между доходностями двух ценных бумаг, которые выведены в представленной работе вместе с выведением формулы дисперсии для суммы дисперсий случайных величин:

Коэффициент корреляции:

, где

- коэффициент корреляции между двумя акциями

Коэффициент ковариации

В связи с этими расчетами Бромвич М. еще раз отмечает, что теория инвестиционного портфеля не предполагает, что средний инвестор действительно будет осуществлять такие сложные расчеты, необходимые для получения коэффициента корреляции для каждой пары ценных бумаг из всего множества, которые ему, возможно, приходится рассматривать. Скорее, она предполагает, что инвестор может каким-то способом прийти к заключению относительно связи между доходностями от двух различных ценных бумаг.

Рис. 4. Связь рентабельности и структуры портфеля

Риск портфеля

или

,

Очевидно, что риск портфеля при разумном сочетании ценных бумаг может быть ниже уровня неопределенности, связанной с каждой отдельной бумагой. Величина снижения риска зависит от степени корреляции между ценными бумагами

Рассмотрим возможные варианты графика дисперсии (волатильности) портфеля при упрощающих предположениях

Напомним, что риск портфеля ценных бумаг двух видов определяется так

или

,

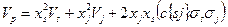где

- коэффициент корреляции двух ценных бумаг

- квадратические отклонения в распределении двух ценных бумаг

Учитывая, что , можно написать:

.

Учитывая, что первые два слагаемые правой части положительны, а коэффициент корреляции изменяется от (+1) до (- 1), дисперсия портфеля должна уменьшаться при движении коэффициента корреляции от (+1) до (- 1).

А) Если коэффициент корреляции равен 1, то есть, в случае линейной положительной корреляции двух ценных бумаг, выражение для дисперсии портфеля примет вид:

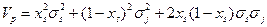
Или

В этом случае дисперсия портфеля, а значит, риск, становятся максимальными.

Если предположить для простоты, что дисперсии двух ценных бумаг одинаковы, или:

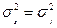, то риск портфеля максимален и представляется прямой горизонтальной линией

Рис. 5. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции (+1)

Б) Если корреляция между двумя ценными бумагами уменьшается до 0, дисперсия становится следующей:

.

при 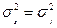или имеем:

.

Найдем точку оптимума, приравняв производную по к нулю.

.

Очевидно, что при , риск достигает минимума (половины риска каждой ценной бумаги)

.

Рис. 6. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции 0

В) Дисперсия (риск) минимальны, когда корреляция двух ценных бумаг равна (-1):

или

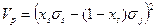
Опять же, если обратиться к нашему упрощающему предположению о равенстве дисперсий двух бумаг

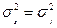или имеем при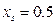

Рис. 7. Связь риска (дисперсии) и структуры для портфеля с одинаковыми дисперсиями двух ценных бумаг и коэффициентом корреляции (-1)

Рис. 8. Связь риска (дисперсии) и доходности для портфеля из двух ценных бумаг

Если мы имеем три ценные бумаги S, Q, J, то риск и доходность инвестиционного портфеля (при известных риске и доходности каждой ценной бумаги) принимает следующий вид

Рис. 9. Связь риска (дисперсии) и структуры для портфеля из трех ценных бумаг

Обратим внимание на существование множества допустимых портфелей, которое определяется точками по границам и внутри криволинейного треугольника. Но легко видеть, что инвестор, ищущий наибольшей доходности при допустимом риске или наименьшего риска при желаемой доходности, выйдет на крайнюю левую границу, которую и называют эффективной границей.

Приведем схему аналитического вывода взаимозависимости риска и доходности для портфеля из двух ценных бумаг.[12]

Пусть:

Тогда из уравнения для доходности находим, что:

Это значение 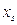подставляем во второе уравнение (уравнение риска портфеля) и т. д. и получаем соответствующее квадратное уравнение:

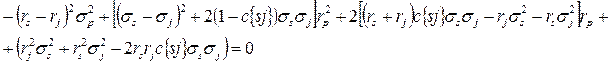Квадратное уравнение может быть исследовано по знаку определителя матрицы, составленной из коэффициентов при членах второго порядка:

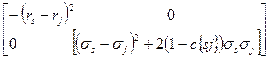
Вывод:

При и кривая является гиперболой.

При и кривая является парой прямых.

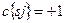При и кривая является прямой.

Для понимания конфигурации допустимого множества решений, рассмотрим крайние случаи:

1. Положим, что коэффициент корреляции двух ценных бумаг равен +1.

Тогда, учитывая, что

можно представить как

,

Получаем при :

или

.

Итак, мы получили отрезок, параметрически заданный на двумерной плоскости следующими уравнениями:

.

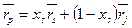
2. Положим, что коэффициент корреляции двух ценных бумаг равен (-1). Тогда аналогичным образом приходим к следующим уравнениям:

Положим . Тогда

и

И при имеем

В конце концов, мы получаем следующую конфигурацию допустимого множества для двух ценных бумаг при изменении коэффициента корреляции от (-1) до (+1).

Рис. 10. Допустимое множество для портфеля из двух ценных бумаг

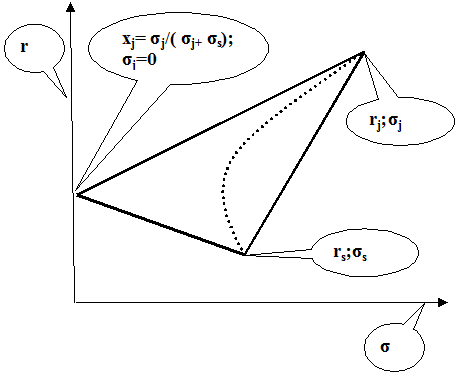
Обоснование.

Рассмотрим произвольную линию уровня , пересекающую эффективное множество портфелей. Оптимальный портфель на этой линии не лежит. Почему? Потому что существуют допустимые портфели, лежащие левее и выше линии .

Рассмотрим линию уровня . Значение функции полезности на линии уровня больше, чем на рассмотренной ранее линии . Однако оптимальный портфель и на ней не лежит. Почему? Потому что на этой линии , вообще, не лежит ни одного портфеля.

Следовательно, оптимальный портфель лежит правее и ниже линии .

Оптимальный портфель лежит между линиями и . Оптимальный портфель лежит на линии проходящей через точку .

Одноиндексная модель У. Шарпа

Модель Г. Марковица требует определения математического ожидания и дисперсии доходности каждой ценной бумаги, а также ковариации между доходами отдельных ценных бумаг. Последняя операция является особенно трудоемкой. Так, например, для анализа 100 акций необходимо рассчитать около 500 ковариаций.

У. Шарпу удалось упростить модель Г. Марковица, предложив, так называемую, индексную модель. Мы рассмотрим простой вариант – одноиндексную модель У. Шарпа.

В основе одноиндексной модели лежит линейная регрессионная модель, которая связывает доходность какой-либо ценной бумаги с тем или иным рыночным параметром (валовым внутренним продуктом, уровнем инфляции, индексом потребительских цен и т.п.). Шарп У. связывал доходность одной ценной бумаги рыночного портфеля с доходностью всего портфеля, в качестве которого принимал пакет акций, входящих в биржевой индекс S&P500.^[16]

Уравнение линейной регрессии строится следующим образом. На основании исторических данных определяются параметры и уравнения:

, где

- доходность -й ценной бумаги в момент ;

- доходность рыночного портфеля в момент ;

- свободный член уравнения, так называемый коэффициент «альфа»;

- коэффициент «бета»

- случайная ошибка (предполагается, что математическое ожидание случайной ошибки равно 0).

Неизвестные параметры и регрессионной модели определяются методом наименьших квадратов из условия минимизации суммы квадратов случайной ошибки:

Необходимо взять производные данного выражения по и , и приравнять их нулю.

Минимум случайной ошибки достигается при следующих соотношениях:

;

Заметим, что минимум суммы квадратов отклонений достигается тогда, когда отклонения считаются от математического ожидания случайной величины, то есть когда теоретические значения доходности ценной бумаги равные математическому ожиданию доходности.

При минимальной случайной ошибке коэффициент «альфа» равен разнице между среднеарифметической доходностью -й ценной бумаги и среднеарифметической доходностью портфеля, умноженной на коэффициент «бета», а коэффициент «бета» - отношению ковариации -й ценной бумаги с рыночным портфелем к дисперсии портфеля. Напомним, что дисперсия равна ковариации ценной бумаги с самой собой.

Напомним также, что коэффициенты ковариации и корреляции связаны следующими соотношениями:

Теперь проведем расчеты необходимых показателей случайных величин (математического ожидания и дисперсии), по имеющимся историческим данным за - моментов времени.

На основе вычисленных показателей случайных величин мы уже можем рассчитать параметры и регрессионного уравнения. Напомним, что:

;

.

Для решения задачи оптимизации портфеля ценных бумаг, подобные расчеты мы должны провести для каждой ценной бумаги из портфеля.

Итак, мы рассчитали параметры регрессионного уравнения, которые дают минимальную величину случайной ошибки. Но нам неизвестна еще эта величина.

Уточним допущения предложенной регрессионной модели:

1. Математическое ожидание ожидаемой случайной ошибки для всех акций равно 0;

2. Дисперсия случайных ошибок для всех акций - постоянная величина;

3. Для каждой акции портфеля отсутствует корреляция между наблюдаемыми на каждом шаге расчета случайными ошибками, то есть ;

4. Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле, то есть ;

5. Отсутствует корреляция между случайными ошибками регрессионного уравнения и рыночной доходности, то есть .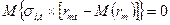

Теперь мы можем корректно рассчитать дисперсию случайной ошибки для каждой ценной бумаги.

По определению дисперсии, . Так как по первому допущению.

Поэтому

Среднеарифметическое значение дисперсии случайной ошибки вычисляется делением на , так как две степени свободы были потеряны при вычислении и .

Теперь мы можем вычислить среднеарифметическое значение доходности и риск (дисперсию) любой отдельной ценной бумаги портфеля с учетом случайной ошибки. Вернемся к нашей основной регрессионной модели:

, где

- доходность -й ценной бумаги в момент ;

- доходность рыночного портфеля в момент ;

- свободный член уравнения, так называемый коэффициент «альфа»;

- коэффициент «бета»

- случайная ошибка (предполагается, что математическое ожидание случайной ошибки равно 0).

.

Итак, подведем итоги:

Становится понятным, почему одноиндексная модель оптимизации портфеля ценных бумаг требует меньше расчетов, чем модель Марковица Г. Дело в том, что отпадает необходимость считать парные ковариации по всем ценным бумагам. Одноиндексная модель предполагает, что показатели любой ценной бумаги зависят только от выбранного индекса, его доходности и риска.

Заметим, что риск отдельной ценной бумаги портфеля раскладывается на две составляющих – риск, связанный с колебаниями портфеля в целом, нестабильностью всего рынка, и риск случайной ошибки регрессионного уравнения, то есть неустойчивости самой бумаги:

Разделим обе части равенства на . Получим:

Первое слагаемое показывает, какую долю в суммарном риске ценной бумаги можно описать с помощью регрессионной модели, а какую следует приписать ее неточности.

Мы рассчитали среднеарифметическую доходность и дисперсию каждой ценной бумаги на рынке. Теперь мы можем определить ожидаемую доходность и риск портфеля, состоящего, например, из ценных бумаг.

Математическое ожидание доходности портфеля из ценных бумаг представляется следующим образом:

, где

- математическое ожидание доходности портфеля из ценных бумаг;

- доля -й ценной бумаги в портфеле из ценных бумаг;

- математическое ожидание доходности -й ценной бумаги.

Подставим в эту формулу выражение для математического ожидания -й ценной бумаги:

Разделим слагаемые на две части, зависимую и не зависимую от рынка:

.

Для упрощения записи мы можем представить рыночный индекс как показатель условной ценной бумаги.

Для этого введем следующее:

, где

и

- портфельная «бета»

Дисперсия портфеля из ценных бумаг:

Подставим в формулу выражения, полученные ранее, а именно:

Получим, с учетом условного введения ценной бумаги:

.

При этом

и

Сформулируем одноиндексную модель У. Шарпа в целом в сравнении с моделью Г. Марковица.

Модель Г. Марковица:

При условиях:

Одноиндексная модель У. Шарпа

.

При условиях:

Модель Тобина

Для дальнейшего упрощения задачи выбора были введены новые допущения. В частности, Тобин Дж. предположил возможность инвестиций в безрисковый актив. Введение безрискового актива существенно меняет конфигурацию допустимого и эффективного множества инвестиционных портфелей

Свойства рынка капитала, принятые в теории инвестиционного портфеля с наличием безрискового актива, частично повторяют предпосылки модели Г. Марковица.

1. Все инвесторы, хотя бы в неявной форме, при осуществлении выбора своих капиталовложений ориентируются на теорию инвестиционного портфеля. Каждый индивидуум исходит в своих решениях только из прогнозов:

- ожидаемой доходности;

- дисперсий доходности;

- корреляции между доходностями из различных источников.

2. Отсутствуют какие-либо трансакционные издержки и налоговые обязательства, связанные с инвестициями.

3. На рынке существует консенсус относительно перспективы каждой продаваемой и покупаемой ценной бумаги

4. Существуют активы, полностью лишенные риска.

Предположим, что инвестор, обладающий только безрисковыми ценными бумагами, рассматривает вложение части своих средств в приобретение портфеля В, состоящего из набора рисковых ценных бумаг. Если он вложит в портфель В 10% своего капитала, то он сможет ожидать среднюю доходность, равную:

.

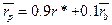Риск, связанный с получением такой доходности будет равен, исходя из формулы суммы дисперсий с учетом весов ценных бумаг, нулевых дисперсии безрисковой ценной бумаги и ковариации безрисковой ценной бумаги с рисковым портфелем:

или

или

Если инвестор 50% своего капитала в рисковый портфель, то доходность и риски станут:

Дополнительная доходность на единицу риска может быть найдена путем деления изменения доходности на изменение общего риска.

В первом случае такой расчет дает:

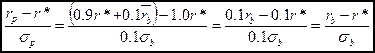
Аналогичный результат получается и для второго случая (50%).

Итак, мы приобретаем дополнительный доход за счет получения дополнительного риска.

Таким образом, общая доходность безрисковой ценной бумаги и портфеля рисковых ценных бумаг может быть представлена следующим образом:

или

Эта прямая линия называется линией рынка капитала.

Выражение 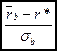можно рассматривать как рыночную цену риска. Или иначе, можно сказать, что необходимый доход от любой комбинации безрисковой ценной бумаги и портфеля рисковых ценных бумаг может быть определен как:

,

где

- рыночная цена риска.

Рис. 12. Связь доходности и риска портфеля в модели Тобина

Приведем более формальное изложение проблемы. Предположим, что эффективное множество состоит только из рискованных ценных бумаг .

Также на рынке существует безрисковый актив .

В силу вогнутости множества существует не более одной касательной к множеству , проходящей через точку .

Рассмотрим случай существования касательной. Обозначим ее через , а точку касания – через .

Теорема 1. Луч является допустимым и эффективным множеством портфелей, состоящих из бумаг .

Доказательство.

Исследуем множество допустимых портфелей. Пусть

,

,

при .

Через обозначим портфель, состоящий только из рискованных ценных бумаг , доли которых такие же, как и в портфеле . В этом случае . Легко подсчитать, что

Тогда

Ожидаемые доходность и риск портфеля равны:

(1)

Так как , то полученные параметрические уравнения (1) для и задают луч на плоскости . Следовательно, портфель находится на луче .

Портфель , состоящий из бумаг , является допустимым тогда и только тогда, когда существует допустимый портфель (то есть портфель с доходностью и риском ) такой, что .

Дело в том, что приобретение безрисковой бумаги допустимо по первоначальному допущению, а ввиду выпуклости допустимого множества точки, лежащие на отрезке, проходящем через допустимые точки множества, также допустимы. Если предположить возможность не только покупки, но и выпуска безрисковых ценных бумаг, то допустимы все точки на луче, проходящем через две допустимые точки.

Другими словами, точка , является допустимой, если допустимы точки и .

Значит, портфели, лежащие на луче , являются допустимыми, так как