Свойства выборочного среднего и выборочной дисперсии

1. Свойства .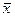

Свойство 1. Выборочное среднее 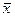является состоятельной оценкой гене­рального математического ожидания m= МX, что следует из предельной тео­ремы Чебышёва:

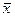
(3.12)

Свойство 2. 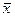является несмещенной оценкой m:

. (3.13)

Свойство 3. 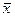не является робастной оценкой т, так как в своем составе имеет крайние элементы вариационного ряда.

Свойство 4. (3.14)

Этот результат означает, что с ростом n рассеяние 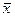уменьшается обратно пропорционально n .

Аналогично доказывается, что выборочный начальный момент 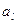поряд­ка l также является состоятельной и несмещенной оценкой генерального на­чального момента порядка l:

(3.15)

Свойства оценок для m и 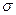в случае нормального распределения

Свойства оценок математического ожидания т.

Рассматриваем 4 выборочных характеристики 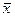, med, t_q, t_R. Так как нор­мальное распределение 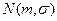- симметричное, то эти выборочные характе­ристики являются оценками m. Действительно, выборочная ме­диана med является оценкой генеральной медианы Ме, полусумма выбороч­ных квартилей является оценкой полусуммы генеральных квартилей 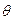_Q, а так как m = Ме = 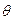_Q, то все они оценивают m. Оценка в силу симметричности конструкции также оценивает m. Все эти оценки состоятельные и несмещенные, t_q и med являются робастными оценками, 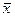и t_R - нет. Относительная эффективность этих оценок различна. При n > 4 имеют ме­сто неравенства

(3.20)

Доказано, что для нормального распределения при известном а выборочное среднее 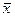является эффективной оценкой параметра m [11].

Свойства оценок среднего квадратического отклонения .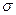

Рассматриваем 4 выборочных характеристики: - интерквартильная широта,

R=x_max -x_min - размах. Все они характеризуют рассеяние, но являются смещенными оценками 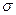, выражаются через 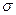, следовательно, после нормирования, означающего де­ление на соответствующий нормирующий коэффициент

, эти характеристики станут несмещенными оценками 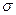. Таблица нормирующих коэффициентов приведена в приложении (таблица VII).

Образуем несмещенные оценки :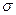

Нормированное среднее квадратическое отклонение s’=s/k_s(n); k_s(n)= . Нормированное среднее абсолютное отклонение d^*=d/k_d(n).

Нормированная интерквартильная широта q^*=q/k_q(n).

Нормированный размах R^*=R/k_R(n).

Все эти оценки - состоятельные [11], qявляется робастной оцен­кой, остальные - нет. Относительная эффективность этих оценок различна, так как различны их дисперсии. При n > 6 имеют место следующие неравенства [11]:

Свойства выборочной дисперсии

Свойство 1. Выборочная дисперсия является состоятельной оценкой гене­ральной дисперсии:

Свойство 2. Вспомогательная формула для выборочной дисперсии

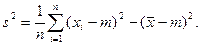(3.17)

Свойство 3. Выборочная дисперсия - смещенная оценка генеральной дисперсии с отрицательным смещением -

(3.18)

Вследствие смещённости выборочной дисперсии возникает задача создания несмещённой оценки дисперсии. Так как 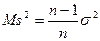, то смещение можно устранить, умножив на множитель 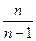: (3.19)

является несмещённой оценкой . Действительно,

В заключение заметим, что не является робастной оценкой .

7. Метод максимального правдоподобия.

Метод максимального правдоподобия, созданный Фишером (Р. Фишер -англ. математик, 1890-1962), является достаточно универсальным и плодотвор­ным методом оценивания.

Пусть имеется выборка (x₁,x₂,…x_n) из генеральной совокупности с плотно­стью вероятности f(x, , содержащей один неизвестный параметр 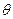. Выборка является n -мерной случайной величиной, компоненты x_i которой взаимно независимы, одинаково распределены с плотностью f(x, . Тогда плотность распределения n-мерной случайной величины (x₁,x₂,…x_n) будет равна

(3.23)

Эта функция называется функцией правдоподобия для рассматриваемой выбор­ки.

Будем считать 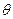переменной неслучайной величиной, а элементы (x₁,x₂,…x_n) выборки фиксированными, так как выборка фактически осущест­влена. Если придавать 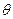различные значения, то естественно ожидать, что плотность 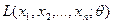примет максимальное значение в случае, когда 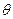окажется равным истинному его значению, так как при других значениях 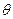ме­нее вероятно за один раз получить именно данную выборку.

Эти интуитивные соображения приводят к тому, что за оценку 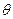берут та­кое значение , при котором функция правдоподобия достигает максимума. Технически (так как L состоит из произведений) удобнее искать max lnL (точка , дающая максимум lnL, дает и максимум L). Итак, для отыскания имеем уравнение

(3.24)

которое называется уравнением правдоподобия, а его решение , зависящее от элементов выборки, оценкой максимального правдоподобия.

При выполнении достаточно общих условий оценки максимального правдо­подобия являются состоятельными и асимптотически эффективными. В общем случае они являются смещенными [10]. В случае, когда генеральная плотность вероятности содер­жит k параметров, вместо одного уравнения правдоподобия решается система уравнений

(3.35) Пример. Рассмотрим показательный закон с плотностью

Функция правдоподобия при х > О имеет вид

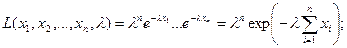
Отсюда

Оценки максимального правдоподобия и метода моментов параметра по­казательного

Замечание. Выше рассмотрены два наиболее употребительных на прак­тике метода получения оценок параметров закона распределения - методы мо­ментов и максимума правдоподобия. Существуют и другие методы, освещен­ные в литературе. Назовем еще методы квантилей, минимума хи-квадрат, наи­меньших квадратов, наименьших абсолютных отклонений, минимакса [10,11].

8. Распределение средней арифметической для выборок из нормальной совокупности.

9. Распределение Стьюдента.

10. Распределение дисперсии в выборках из нормальной генеральной совокупности

11. Распределение Хи-квадрат Пирсона.

12. Понятие доверительного интервала