Категории:

Дом Здоровье Зоология Информатика Искусство Искусство Компьютеры Кулинария Маркетинг Математика Медицина Менеджмент Образование Педагогика Питомцы Программирование Производство Промышленность Психология Разное Религия Социология Спорт Статистика Транспорт Физика Философия Финансы Химия Хобби Экология Экономика Электроника

Вопрос 1. Формальные исчисления. Выводы в исчислении. Теорема исчисления. Разрешимые и непротиворечивые исчисления.

ВОПРОСЫ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ И ТЕОРИИ АЛГОРИТМОВ (АВТФ, III семестр)

1. Формальные исчисления. Вывод в исчислении. Теорема исчисления. Разрешимые и
непротиворечивые исчисления.

2. Основные эквивалентности ИВ. Теорема о замене. Дизъюнктивная и конъюнктивная
нормальные формы.

3. Исчисление высказываний (ИВ): формулы, аксиомы и правила вывода. Понятие
доказательства, дерево доказательства. Теорема о дедукции.

4. Семантика исчисления высказываний. Непротиворечивость ИВ. Таблицы
истинности. Общезначимые и выполнимые формулы. Теорема о полноте.
Разрешимость ИВ.

5. Семантическое дерево. Алгоритм Квайна и алгоритм редукции проверки
общезначимости формул.

6. Метод резолюций в ИВ. Метод согласия. Метод резолюций для хорновских
дизъюнктов.

7. Алгебраические системы. Формулы сигнатуры Σ. Подформулы. Свободные и
связанные переменные. Предложения. Истинность формулы на элементах
алгебраической системы.

8. Общезначимые и выполнимые формулы. Теорема об общезначимости формул
сигнатуры S, соответствующих общезначимым формулам ИВ. Выполнимое множество
формул. Теорема компактности.

9. Исчисление предикатов сигнатуры Σ (ИП ^Σ)^: аксиомы и правила вывода, доказуемые
формулы. Теорема о дедукции. Тождественно истинные формулы. Теорема Гёделя о
полноте. Теорема о непротиворечивости ИП ^Σ. Теорема о существовании модели.

10. Основные эквивалентности ИП ^Σ - Теорема о замене. Пренексные и клазуальные
нормальные формы.

11. Элементарные теории. Система аксиом теории. Полные теории. к-Категоричные
теории. Теорема о полноте к-категоричной теории. ω-Категоричность теории плотного
линейного порядка.

12. Система аксиом арифметики Пеано. Нестандартные модели арифметики. Теорема
Дедекинца-Пеано.

13. Подстановка сигнатуры Σ. Композиция подстановок. Унификатор и наиболее
общий унификатор. Алгоритм унификации. Теорема об алгоритме унификации.

14. Бинарная резольвента и резольвента дизъюнктов сигнатуры Σ. Резолютивный
вывод. Полнота метода резолюций.

15. Проверка непротиворечивости множества предложений методом резолюций и
построение моделей. Формализация свойств и их доказательство с помощью метода
резолюций. Принцип логического программирования.

16. Понятие алгоритма, основные признаки алгоритма. Вычислимые функции и тезис
Чёрча.

17. Определение машины Тьюринга.

18. Основные машины Тьюринга. Операции над машинами Тьюринга.

19. Вычисление функций на машинах Тьюринга.

20. Понятие примитивно рекурсивной функции, основные примеры.

21. Примитивно рекурсивные отношения, основные преобразования над ними,
примеры примитивно рекурсивных отношений.

22. Нумерации n-ок натуральных чисел примитивно рекурсивными функциями.

23. Частично рекурсивные и рекурсивные функции. Теорема об элиминации
примитивной рекурсии.

24. Вычислимость частично рекурсивных функций на машинах Тьюринга.

25. Частичная рекурсивность функций, вычислимых на машинах Тьюринга.

26. Универсальные ЧРФ. Теорема об универсальности. Теорема о существовании ЧРФ,
недоопределимой до рекурсивной функции. Теорема Раиса.

27. Гёделевская нумерация формул, аксиом и правил вывода исчисления предикатов.
Рекурсивно перечислимые множества. Разрешимые и неразрешимые теории. Теорема
Гёделя о неполноте арифметики. Теорема Чёрча о неразрешимости исчисления
предикатов.

28. Временная и ленточная сложности машины Тьюринга, вычисляющей заданную
функцию. Теоремы о верхней границе сложности вычислений. Теорема об ускорении.

29. Класс эффективно вычислимых функций. Метод сводимости.

30. Понятие переборной задачи. Универсальные переборные задачи, примеры.

31. Основные алгоритмы сортировки и их сложность.

32. Детерминированные и недетерминированные конечные автоматы, связь между
ними.

33. Неклассические логики.

Вопрос 3. Основные эквивалентности (ИВ) формулы ,аксиомы и правила вывода. Понятия док-ва ,дерево док.. теор. о дедукции.

Алфавит.

-проиозициональные переменные Q₀,Q₁,…,Q_n,… ; A,B,C,…

-логические символы или связки Λ,v,→, ┐,├- символ следования

-вспомогательные символы:( ),

Фор-лы ив – слово алфавита ив ,кот. Опр-ся по инд.:

1)любая проп. перем. явл. ф-лой(анотамарная или элементарная ф-ла) A_n,Q₇

2)если φ,ψ –формулы ,то (φ Λ ψ),( φVψ), ( φ→ψ), ┐φ – ф-лы

Секвенции ИВ

φ₁ ,…,φ_n├ ψ,Г├ ψ

-Г├(из Г можно вывести противор.инф)

-├ общее противоречие ; φ₁ ,…,φ_n –посылки,ψ- заключение;схема аксиом: φ├ φ

Правила вывода:

1) (Г├ φ;Г├ ψ)/ (Г├(φ Λ ψ)) ; 2) (Г├(φ Λ ψ))/ (Г├φ) ; 3) (Г├(φ Λ ψ))/ (Г├ ψ) ;

4) (Г├ φ)/( Г├( φVψ)) ; 5) (Г├ ψ )/( Г├( φVψ)) ; 6) Г,φ├ ψ;Г,x├ ψ;Г├ φVψ/Г├ ψ;

7) Г,φ├ ψ/ Г├( φ→ψ) ; 8) Г├φ, Г├( φ→ψ)/ Г├ ψ ; 9)Г, ┐φ├/ Г├φ ; 10) Г├φ; Г├ ┐φ/ Г├;

11) Г₁, φ, ψ,Г₂├x/ Г₁, ψ,φ, Г₂├x ; 12) Г├φ/ ψ ├ φ;

Дерево секвенций

1)если S – секв. ,то S – дерево секвенций

2)если D₀,…,D_n-деревья ,S –секв., то D₀,…,D_n/S-дерево секвенций

Дерево D раз. Докозат. Если все начальные секвенции явл. аксиомами,а переходы осуществ. По правилам вывода.

Теорема о дедукции. Если Г,φ├ ψ,то Г├( φ→ψ) (правило 7) следствие секв. φ₁ ,…,φ_n├φ доказуема ó дказуема ф-ла (φ₁→( φ₂→…( φ_n→ ψ)…))

Вопрос 6. Метод резолюций в ИВ. Правило согласия. Метод резолюций для

Хорновских дизъюнктов.

D1=D’1 v A, D2=D’2 v`A тогда резольвента: res(D1,D2)=D’1 v D'2( по литере А),

а res (A, `A) (по литере А ) = 0

УТВЕРЖДЕНИЕ: Если res(D1,D2)=D’1 v D'2 существует, то секвенция

D1, D2 ├ res(D1,D2) доказуема

ДОКАЗАТЕЛЬСТВО: D1=1, D2=1 => в D1 или D2 истиной является другая литера=>

res(D1,D2)=1

S={D1,…,Dm}- множество дизъюнктов, последовательность дизъюнктов f1, …. , fn называется резолютивным выводом из множества S, если для любого i выполняется

fi ? S или fi=res(fj , fk), где j, k <I

ТЕОРЕМА (о полноте метода резолюций)

Множество дизъюнктов S - противоречиво( секвенция S├ доказуема) ó существует резолютивный вывод из S ? который заканчивается 0 (противоречием)

ТЕОРЕМА Если S – множество дизъюнктов содержащее все свои резольвенты, то S противоречиво ó 0 ? S

Правило СОГЛАСИЯ

K1= K’1 ٨ A , K2= K’2 ^ ‾A , res по А(K1, K2) = K’1 ^ K’2, res (A,A)=1

ТЕОРЕМА о полноте

Множество конъюнктов S = {K1, … ,K2} общезначно, (т е ╞ K1 v …. V Km)

ó существует вывод из S по правилу согласия, который заканчивается на 1 .

ХОРНОВСКИЕ ДИЗЪЮНКТЫ

Дизъюнкт D называется Хорновским, если D содержит не более одной положительной литеры

S – множество хорновских дизъюнктов. Противоречиво ли S?

0 ¢ S => выбираем из S факт , дизъюнкт С, содержащий P

res (C , P) = вычеркиваем из С литеры P

S:=(S\{C})U({res(C,P)}, процесс продолжается до вывода 0, или стабилизируется на некоторое множество Хорновских дизъюнктов, не содержащее 0

Вопрос 9.

Зафиксируем некоторую произвольную сигнатуру S и опр-им исчисление предикатов сигнатуры S( ИП^S ). Аксиомами ИП^Sявл. следующие секвенции:

1. φ ├ φ, φ-формула ИП^S

2. ├ x ≈ x, x –переменная

3. x ≈ y, (φ)^Z_X├(φ)^Z_Y_,x,y,z-переменные, φ-формула ИП^S, удовлетворяющего условию на запись (φ)^Z_x и (φ)^Z_Y

Правила вывода ИП^S таковы:

1. ; 2. ; 3. ; 4. ; 5.

6. ; 7. ; 8. ; 9.

10. ;11. ;12. ;

13. , где x не входит в члены Г свободно; 14. ; 15.

16. , где х не входит в и члены Г свободно.

Следующие секвенции доказуемы:

1. ├ $ x1,…,$xn φ

2."x1, … , "xn ψ├ (ψ)x1,…, xn

Теорема о дедукции. Если Г U {φ,ψ} – мн-во формул ИП^S, то из Г,φ-|ψ следует Г-| φ→ψ.

Теорема Гёделя о полноте. Формула φ исчисления ИП^S доказуема тогда и толь тогда, когда φ тождественно истинна.

Исчисление ИП^S непротиворечиво, т.е. не все формулы ИП^S доказуемы в ИП^S.

Док-во:

S=(├ x ≈ x)(тождественно ложная формула)

=> ╞ S => по т. о полноте S недоказуемо => ИП^S непротиворечиво.

Пример.

{ F₁(z)/x, y/z} - подстановка сигнатуры ∑ = { F₁₁⁽¹⁾}.

{ C₁/x, F₂⁽⁹⁾/y, F₁( F₂(C₁))/z} – подстановка сигнатуры ∑ = {C₁⁽⁰⁾, F₂⁽¹⁾, F₁⁽¹⁾, C₁⁽⁰⁾}.

Пусть Ө = {t₁/x₁, ..., t_n/x_n} подстановка сигнатуры ∑. W Ө - множество получаемое из W с помощью одновременной подстановки вместо x₁, ..., x_n термов t₁, ..., t_n.

Пример.

Ө = { C₁/x, F(C₂)/y, y/z }

t = F₁ (x, y, z), тогда t Ө = F₁(C₁, F(C₂), y)

Q = F (x, C₁, z)

Q Ө = F₁(C₁) ≈ F₁(C₁, C₁, y)

Ө = {t₁/x₁, t_n/x_n}

λ = { g₁/y₁, ... , g_n/y_n}

Ө λ = { t₁, λ/x₁,..., t_nλ/x_n, g₁/g_n,..., g_n/y_n}

Если y_i принадлежит { x₁ ... x_n}, то g_i/y_i - вычёркиваем

Если t_iλ = x_i , то t_i λ/x_i – вычёркиваем

Пример.

Ө = { F₁(y)/x, z/y}; λ = {C₁/x, C₂/y, y/z}

Ө λ = {F₁(y)λ/x, zλ/y, C₁/x, C₂/x, y/z} = {F₁(C₂)/x, y/y, y/z} = {F₁(C₂)/x,y/z}

Өz = Ө любая Ө

Ө ( λ μ ) = (Ө λ ) μ для любых μ, λ, Ө

Определение:пусть Ф = {φ_{1, ....} ,φ_n} – множество формул сигнатуры ∑; Ө - подстановка сигнатуры ∑. Ө называется унификатором множества Ф, если φ₁ Ө = … = φ_n Ө.

Пример.

Ф = {P (C₁,y), P(x₁) = C₂} можно заменять только переменные

Ө = {C₁/x, F(C₂)/y} – унификатор множества Ф

Определение:множество формул называется унифицируемым, если для него есть унификатор.

Определение: унификатор σ для множества {φ_{1, ....} ,φ_n} называется наиболее общим унификатором (НОУ), если для любого другого унификатора Ө существует λ такая что Ө = σλ.

Определение: пусть W = {φ_{1, ....} ,φ_n} – непустое множество атомарных формул. Множеством рассогласований множества W называется множество термов t₁, ..., t_n, где t_i входит в φ_iи начинается с символа стоящего на первой слева позиции в φ_i; на которой не для всех формул φ_{1, ....} ,φ_n находится одинаковый символ.

Пример.

W = { P(x), F(y, z), P(x, c), P(x |= (y, F₁(z)))}

Найдём множество рассогласований Д_l = {F(y, z), C |= (y, F₁(z))}

Алгоритм унификации

Определяет, унифицируемость множества атомарных формул, или нет, и если унифицируемо, то находим наиболее общий унификатор.

Дано W –множество атомарных формул.

k = 0, w₀ = w, σ₀ = ∑.
Если | w_k | = 1 следовательно, множество W унифицируемо в качестве НОК = σ_k. Иначе находим Д_k – множества рассогласований множества W_k.
Если Д_kсодержит переменную x_k и терм t_k не содержащий x_k, то переходим к 4. иначе – остановка, W не унифицируемо.
σ_k+1 = σ_k {t_k/x_k}, W_k₊₁ =W_kσ_k₊₁, k →k + 1 переходим к шагу 2.

Теорема:если W унифицируемо, то алгоритм унификации закончит работу на втором шаге и последняя подстановка σ_k является НОУ.

Пример.

W = { P ( z, x, F₂(F₁(y))), P(z, F₂(z), F₂(n))}

1. W₀= W, σ₀ = ∑.

2. | W₀| ≠ 1, тогда Д_k = {c, z}

3. 4. σ₁= σ₀, {c/z} = {c/z}

W₁ = {P (e, x, F₂(F₁(y))), P(e, F₂(e), F₂(n)}

Следовательно 2 | W₁| ≠ 1, тогда Дk = {x, F₂(e)}.

Вопрос 14.

Литера сигнатуры : атомарная формула или ее отрицание.

Дизъюнкт сигнатуры : литера или дизъюнкт литера сигнатуры

А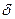; … A- дизъюнкт в ИВ

А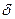, A- атомарные формулы (дизъюнкт сигнатуры )

P(c₁x₁*h (y,z)) h(g,(x),y) z

Ф-дизъюнкт сигн-ы вида

₁ … n X или ₁ … n ,

где ₁ – атомарные форм-ы сигн-ы

Пусть 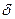- НОУ для { ₁ ,…, n }

Тогда ₁ 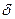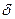наз-ся ??????? формулы Ф

Ф = P(x) P(F(y)) P₂(x)

= {F(y) / x}

Ф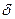= P(F(y)) P₂(F(y))

Ф₁,Ф₂ – два дизъюнкта, не имеющих общих переменных.

L₁- литера в Ф₁

L₂`=L₂- литера в Ф₂

Если L₁и L₂имеют НОУ , то дизъюнкт, получ-ый из Ф₁ Ф₂ вычерчиванием L1 и L2 наз. бинарной резольвентой дизъюнктов Ф₁ и Ф₂

L₁и L₂– отрезаемые литеры

Если Ф₁ = L₁, Ф₂ = L₂, то бинар.рез. Ф₁ и Ф₂= 0

Если Ф₁ и Ф₂имеют общие переменные, то после замены общих переменных в Ф₂ на новые обр. ???? Ф₂

Бин. рез. Ф₁ и Ф₂= бин. рез. Ф₁ и Ф₂^`

Ф₁= P₁(x) P₂(y)

Ф₂= P₁(c) P₃(x)

Ф₂^`= P₁(c) P₃(y)

L₁ = P1(x)

L₂ = P₁(c), L₂= ???(c) P₁(c) = L₂^`

= {c/x}

Бин. рез. Ф₁ и Ф₂= P₁(с) P₂(с) P₁(c) P₃(y) = P₂(с) P₃(y)

Резольвента дизъюнктов Ф₁ и Ф₂

(res (Ф₁,Ф₂)):

- бин. рез Ф₁ и Ф₂

- бин. рез. склейки Ф₁ и Ф₂

- бин. рез. Ф₁ и склейке Ф₂

- бин. рез. склейки Ф₁ и склейки Ф₂

Ф₁ = P(x) P(F(y)) P₁(F₁(y))

Ф₂ = P(F(F₁(c₁))) P₂(c₂)

res (Ф₁,Ф₂) = ?

склейка Ф₁:Ф₁` = P(F(y)) P₁(F₁(y))

L1 = P(F(y))

L2 = P(F(F₁(c₁)))

res (Ф₁`,Ф₂) = P₁(F₁(F₁(c₁))) P₁(c₂)

S – мн-во дизъюнктов.

Результативным выводом формулы Ф и S наз. полслед-ть дизъюнктов Ф1, … , Ф_к, где Ф_к = Ф

и каждый дизъюнкт Фi или принадл. S, или явл-ся резольвентой дизъюнктов, предшествующих Фi.

Ф(x₁,…,x_n)

x₁… x_n Ф(x₁,…,x_n) универсальное замыкание формулы Ф (x₁,…,x_n)

Теорема о полноте метода резолюций для ИП

Если S – мн-во дизъюнктов или , то мн-ва универсальных замыканий формулы из S противоречиво 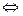сущ. рез. вывод из S.

Сложно вычислимые функции

Теорема Для любой Р.Ф. h(x) существует Р.Ф. f(x) т.ч r_f ={0,1) и для любой машины Т, вычисляющей f(x), начиная с некоторого X выполняется условие t_T(x) > h(x)

Теорема об ускорении

Для любой Р.Ф. r(x) сущ. Р.Ф. f(x) с условием, что r_f ={0,1), т.ч какова бы ни была машина Т_i, вычисляющая ф-ию f(x) найдется машина T_j, вычисляющая эту функцию с условием, что t_Ti(x) > r(t_Tj(x)), начиная с некоторого x

Пример.

r(x) = 2^x

t_Tj < log₂(t_Ti(x))

t_Tk< log₂log₂(t_Ti(x))

Вопрос 29. Эффективности вычислений:

Z={z} – массовая задача

Исходные данные представленные в виде слов Р в конечном алфавите, зависящих от z.

Размерность - длина слов Р, кодирующего исходные данные задачи z.

Пример Вектор значений булевой функции.

Массовая задача решается эффективно (просто), если существует полином Q(x), такой что время решения каждой задачи z Ć Z не превосходит Q(e(z))

Эффективное вычисление – вычисление с полиномнальной сложностью.

Переборная задача 2^e⁽^z⁾

Метод сводимости:

Массовая задача Z={z} полиномиально сводится к массовой задачи Z`={z`}, если существует словарная функция F, которая по произвольной задаче z Ć Z строит задачу F(z)=z`Ć Z`, что задача z имеет положительные ответ тогда когда z` имеет положительный ответ и время вычисления F(z) ограничено значением Q(e(z)), где Q(x) – некоторый полином, зависящий от массовых задач Z и Z`, но не от некоторых задач z и z`.

Пример. Задача о МДНФ сводится к задаче покрытия единиц множествами, образование К – мерной карты (карты корно).

Определение переборной задачи

Массовая задача Z называется переборной, если она может быть сформулирована в след. виде: по заданному значению z Ć Z выяснить, существует ли y, размерность которого e(y) не превосходит полинома e(z) и такой, что выполнено свойство R(z,y), поверяемое на машине Тьренга за время, ограниченное полиномом от e(z)+e(y). Перебор объектов y до тех пор, пока не выполнится R(z,y)

Число переборов растет по экспоненте.

1. z четно? z/y=2 Если y найден z=2y

2. Кодовый замок y – ключ.

3. f,g –булевы функции f=g

y=(q₁…….q_n) f(q₁…….q_n)=g(q₁…….q_n)

Переборная задача Z называется универсальной или полной, если любая ПЗ полиномиально к ней сводится.

1. Задача выполнимой булевой функции

2. Задача о полном подграфе

3. Задача о вершинном покрытии

Множество вершин таких, что каждое ребро графа инцедентно к некоторой вершине из этого множества.

4. Задача о существовании гамельтонова цикла в гафе.

5. Задача о раскраске графа.

6. Задача о изоморфном подграфе (для заданных графов G и G` установить существует ли в G` подграф, изоморфный графу G).

Вопрос 30.Понятие переборной задачи. Универсальные переборные задачи. Примеры.

Массовая задача Z называется переборной, если она может быть сформулированная следующим образом: по заданному zÎZ выяснить, сущ. ли такой y, размерность которого l(y) не превосходит Q(l(z)) полинома от l(z) и такой, что выполнено свойство R(z,y), проверяемое на подходящей МТ за время, не превосходящее полинома Q(l(z)+l(y)).

Решается перебором объектов y до тех пор, пока не выполнится R(z,y)

Число переборов растет экспоненциально от y.

Переборная задача Z⁰ называется универсальной, если любая переборная задача полиноминально к ней сводится.

Примеры.

1) Задача о выполнимости булевой ф-ии

2) Задача о полном подграфе (по заданному подграфу G выяснить, имеется ли в G полный К-вершинный подграф)

3) Задача о вершинном покрытии (по заданному графу G и числу K, узнать, имеется ли вершинной покрытие G мощности K)

4) Задача о существовании гамильтонова цикла в графе

5) Задача раскраски графа K цветами

6) Задача об изоморфном подграфе (для заданных графов G и G’ установить, существует ли в G’ подграф, изоморфный графу G)

Предикатные логики

1. Многосортная логика первого порядка.

ИП – логика первого порядка

"x$n >= 1 (nx = 0) – невыразима в ИП

Многосортная логика сводится к односортной.

2. D – логика.

D – бесконечн. => не вып. теорема компактности.

3. Бесконечные логики.

Допускаются бесконечные ф-лы. Т. компактности неверна.

4. Логика с новыми кванторами.

5. Темпоральная (временная) логика.

Рассматривается принципиальная возможность или невозможность события, а также причинно-следственные связи между событиями.

Требования корректности.

Требования жизнеспособности.

Атомарные ф-лы – ф-лы ИП, включающие операции над z (временные операции).

Темпоральные операторы:

О(“Next”) – следующее событие

U(“Until”) – длительность истинности некоторого св-ва, относительно другого св-ва.

Кванторы: «Всегда», «Когда-нибудь всюду», «Когда-нибудь где-то»