Численный метод расчёта ирисовых пружин

Для построения упругой нелинейной характеристики P=P(x) применим метод последовательных нагружений [21.22], задавая приращения осевой нагрузки . На каждом шаге нагружения будет решаться каноническая система уравнений метода сил, которую можно рассматривать как частный случай способа переноса граничных условий. Такое исследование необходимо для достижения основной научной цели диссертации – а именно для метода механической прогонки. Суть метода прогонки заключается в переносе граничных условии.

Воспользуемся механической моделью ирисовой пружины (рисунок 2.6). Решением системы четырёх уравнений метода сил

(2.33)

Определим приращения реакций в шарнире О :- 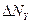, , , 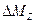. Эти приращения соответствуют реакциям 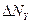, , , 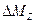на рисунке 2.6 Коэффициенты системы (2.33) получим численным подсчетом интегралов Мора от перемножаемых эпюр моментов единичных силовых факторов, соответствующих искомым реакциям и силе Р

(2.34)

При этом длину l бруса разобьем на n одинаковых участков . В пределах каждого участка изгибающие и крутящий моменты можно считать постоянными. Для i-го участка бруса, определяемого углом , текущее значение смещения относительно плоского положения ирисовой пружины обозначим . Обозначим в сечении участка : -минимальный момент инерции на изгиб вокруг радиальной оси ; -максимальный момент инерции на изгиб вокруг оси ; -крутильный момент инерции 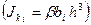. Здесь и 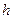соответственно ширина и толщина упругого элемента на -м участке, -малоизменяемый коэффициент, зависящий от отношения , -угол наклона -го участка к плоскости , определяется из соотношения: ; -центральный угол упругого элемента.

Таким образом, можно задавать переменными ширину и форму прогиба упругого элемента, как в виде функции, так и в виде массива данных ( ). Радиус срединной линии R, толщину упругого элемента h и центральный угол упругого элемента можно считать постоянными величинами.

После определения приращений реакций в шарнире O из (2.33) определяются приращения реакций в жёсткой заделке- При этом решаются шесть уравнений статического равновесия пространственного бруса ОВА .

Далее численным подсчетом интегралов Мора определяется приращение прогиба -го участка : (2.35) .

Здесь: 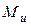- изгибающиймомент вокруг радиальной оси; - изгибающий момент вокруг оси - крутящий момент в -м сечении упругого элемента в зависимости от найденных приращений реакций и активной силы . Соответственно изгибающий момент вокруг радиальной оси, изгибающий момент вокруг оси крутящий момент в j-м сечении от единичной силы, приложенной на i- участке упругого элемента (рисунке 2.6).

Тогда новое значение смещения -го участка относительно плоского положения ирисовой пружины выразится через значение предыдущего шага в виде

= - . (2.36)

Величина перемещения Х ирисовой пружины после каждого шага нагружения определится через предыдущее значение перемещения Xn

в виде

(2.37)

где - приращение перемещения ирисовой пружины, определенное с помощью (2.35).

Величина смещения опорных колец равна

(2.38)

где Xc - исходная величина смещения опорных колец (величина заневоливания).

Полные значения реакций после нагружения силой определяются через предыдущие значения реакций в виде

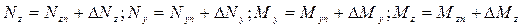
Аналогично определяются полные реакции в заделке А:

Далее следует процедура вычисления активной искомой нагрузки на один упругий элемент ирисовой пружины Р. Для этого определим полный вектор боковой реакции в шарнире О

(2.40) и угол между ним и осью Z из соотношения

(2.41)

Наконец из уравнения равновесия моментов относительно оси S , проходящей через точку А перпендикулярно плоскости , определим Р, соответствующее значению X из (2.36)

(2.42)

На этом цикл вычислений одного шага нагружения заканчивается и начинается новый шаг нагружением

За счет уменьшения смещения опорных колец до нудя (плоское положение) и далее при достижених отрицательные величин функция Р=Р(x)будет иметь нелинейный характер.

Описанный алгоритм был реализован в виде программы на языке

«Бейсик». Расчёты на ЭЦВМ проведены для ирисовых пружин сейсмоприёмника СВ-5, изготовленных из сплава «Камелон» (медно-никелевый сплав, ) с размерами:

h=0,13 мм ; Хс =4,5 мм; b=1,25 мм ; R=15,9 мм ; =1,8 рад. (2.43)

Исходное значение величины заневоливания (Xc =4,5 мм) полученоза счёт осевого смещения наружного и внутреннего опорных ко­лец на величину 5 мм в жёсткой заделке и выдержке при температуре старения 530°С в течении 1 ч 45 мин в вакууме. Таким образом после термообработки произошло упругое обратное деформирование опорных колец на 0,5 мм (10 %), свидельствующее о наличии остаточных внутренних напряжений. На рисунке 2.7 представлены исходная форма срединной линии упругого элемента (кривая 1), полученная в результате натурных измерений и исходная форма, соответствующая закону косинуса (кривая 2).

Эти формы даны в виде деформаций срединной линии по отношению к одному из колец в зависимости от длины этой срединной линии представленной в процентах. Видно, что действительная исходная форма несимметрична относительно середины упругого элемента. Это сказалось на форме прогиба, один из моментов которой (кривая 1а) вычислен на ЭВМ после прохождения опорными кольцами плоского положения. Кривая (вычисленная по М.П.) прогиба упругого элемента 2а соответствует исходной форме по закону косинуса. В этом случае сохраняется исходная симметрия.

Кривая 1 соответствует действительной исходной форме упругого элемента. Кривая 2- исходной форме, заданной по закону косинуса.

На рисунке 2.8 даны расчётные кривые распределения интенсивности напряжений по длине упругого элемента l . Кривая 1 соответствует действительной исходной форме упругого элемента (в момент мм) кривые 2 и 3 - исходной форме по закону косинуса в моменты: мм).

Очевидно, что наибольших значений напряжения достигают в местах перехода упругих элементов в опорные кольца, несколько снижаясь к середине и соизмеримы с пределом упругости ( ). Это подтверждается статистикой поломок пружин, большинство из которых происходит в местах перехода упругих элементов в опорные кольца. Современные требования к ирисовым пружинам геологоразведочных сейсмоприёмников оговаривают пределы усталостной прочности.

Рисунок 2.7 - Форма упругого элемента в результате натурных измерений (сплошные линии) в результате расчетов и при аппроксимации по закону косинуса (штриховые линии) в исходном положении (кривые 1,2) и после перехода плоского состояния

Рисунок 2.8 - Расчетные кривые распределения интенсивности напряжений s_i в зависимости от длины упругого элемента l.

Для обеспечения максимальной прочности ирисовых пружин поперечное сечение упругих элементов выполняют переменным, утолщая их в местах перехода в опорные кольца. Необходимо учесть, что в рабочем состоянии, когда ирисовая пружина приводится в плоское положение, напряжения в середине упругого элемента увеличиваются за счёт увеличения изгибающего момента от бокового усилия .

На рисунке 2.9 представлены результаты расчёта напряжений по длине упругого элемента ирисовой пружины, изготовляемой интеркорпорацией “OYO GEOSPACE” (рисунок 2.10). Очевидно, что в этой пружине заложен принцип равнопрочности. Змееобразная форма придана для удаления резонансной частоты упругого элемента от рабочей частоты прибора.

Реализованный численный алгоритм устраняет затруднения, связанные с учётом сложности исходной и деформированной формы ирисовых пружин при расчёте упругих нелинейных характеристик F=F(x).

Рисунок 2.9 - График изменения интенсивности напряжений s_i в зависимости от длины упругого элемента I ирисовой пружины “OYO GEOSPACE”

Рисунок 2.10 – Ирисовая пружина, изготовленная интеркорпорацией “OYO GEOSPACE”

На рисунке 2.11 представлены упругие характеристики ирисовой пружины с тремя упругими элементами с размерами (2.43). Кривая 1э получена экспериментально для исходной действительной формы 1, показанной на рисунке 2.7. Кривая 1 (рисунок 2.11) получена расчётным путем для той же исходной формы с заданием массива X. Расчётная кривая 2получена для исходной формы, заданной по закону косинуса.

Сравнение кривых рисунка2.11 позволяет сделать вывод, что учёт действительной исходной формы упругих элементов значительно приближает упругую расчетную характеристику к экспериментальной. Аппроксимация же исходной формы упругого элемента, несмотря на незначительные отличия (кривые 1 и 2 на рисунке 2.7, приводит к большим отклонениям расчётной и экспериментальной упругих характеристик. Это видно на рабочей точке упругой характеристики (рисунок 2.11), когда ирисовая пружина с подвешенной инерционной массой сеисмоприёмника m приводится в плоское положение (X=Xc =4,5 мм). Жёсткость ирисовой пружины С, от которой зависит задаваемая собственная частота сейсмоприёмника определяется из соотношения:

(2.44)

Для исходной формы, задаваемой по закону косинуса, жёсткость на рабочей точке принимает отрицательные значения, что является неприем­лемым.

Полученные результаты численного расчёта согласуются с опытом изготовления ирисовых пружин. Несмотря на малый допуск на толщину упругих элементов в пределах нескольких микрон отклонения жёсткости С инесущего усилия составляют десятки процентов. Это объясняется большим полем отклонении формы после термообработки ирисовых пружин. Сказывается также наличие остаточных внутренних усилий.

Однако, использование нелинейных упругих характеристик позволяет значительно уменьшать габариты низкочастотных сейсмоприемников, в массовом количестве применяемых в геологоразведке. Поэтому при сборке сейсмоприёмников ирисовые пружины подбираются по парам со взаимной компенсацией погрешностей. Таким образом представленный по численный алгоритм можно рекомендовать для уточнённого расчёта нелинейных упругих характеристик ирисовых пружин с учётом сложности исходной геометрии.

Необходимо отметить, что как аналитический, так и численный методы в данной работе рассмотрены на примерах расчёта ирисовых пружин с жёсткой заделкой опорных колец. В некоторых типах сейсмоприёмников применяют свободное отпирание опорных колец. В этом случае опорные кольца участвуют в упругих деформациях ирисовой пружины и её нагрузочная характеристика сильно отличается от случая жёсткой заделки. Поэтому для случая свободного опирания в расчётную модель нужно (рисунок 2.2) ввести последовательное соединение упругих элементов, содержащихся в кольцах ирисовой пружины .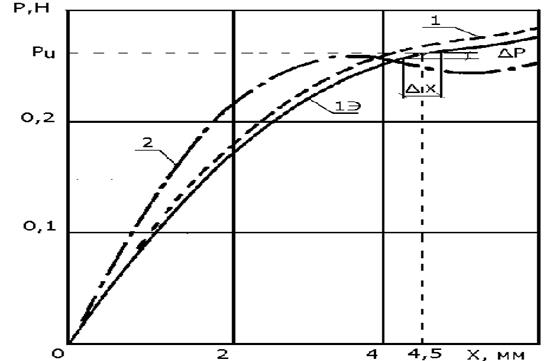

Рисунок 2.11 - Упругие характеристики трехлучевой ирисовой пружины.