Формулировка метода механической прогонки

Дадим определение разработанному алгоритму как варианту метода для расчета механических систем [142-145].

Метод механической прогонки заключается в переносе граничных условий, выраженных в механических параметрах по элементам, на которые условно расчленена механическая система. При этом за счет решения в первую очередь уравнений для ограниченного числа неизвестных внутри каждого элемента последовательно исключается неизвестные параметры внутри всей механической системы.

При реализации данного метода на ЭВМ, параметры прогонки для оболочечных конструкций удобно задавать в виде трехмерных массивов.

Основное измерение массива равно размерности вектора искомых параметров (4.51). Остальные измерения для большинства параметров можно ограничивать числом два. Это позволяет расчленять конструкции на достаточно большое число элементов (~ 100) при работе на микрокомпьютерах.

Положительные результаты, достигнутые в расчете НДС оболочек с использованием метода механической прогонки, позволяют перейти к применению этого метода для общего случая деформированного твердого тела. Задачи такого типа требуют учета большего числа степеней свободы и соответственно факторов влияния, Обзор современных работ по механике твердого тела [132 –141] показывает, что имеет место проблема роста массива данных при более полном учете факторов влияния. Разработанный алгоритм метода механической прогонки, достоинством которого является экономия памяти ЭВМ, позволит увеличить число факторов влияния.

Выводы по главе.

Сформулирован метод механической прогонки. Достоверность метода подтверждена при расчете напряженно – деформированного состояния оболоченной модели твердого тела.

ГЛАВА 5 Алгоритм метода механической прогонки на основе упругой модели конечных элементов

Упругая модель плоского конечного элемента

Целью настоящей главы является приложение метода механической прогонки к расчету НДС сплошной упругой среды твердого тела. В разрабатываемых алгоритмах для реализации метода необходимо придерживаться тенденции к решению возможно большей части совокупности уравнений на стадии их составления.

Решение части всей совокупности уравнений в процессе обхода элементов уменьшает число разрешающих уравнений и тем самым позволяет сгущать сетку разбиения, уменьшая ее шаг. В результате изменение параметров в пределах элементов приближается к линейному закону. При линейном изменении параметров элементы можно представить упругими механическими моделями.

Рассмотрим построение упругой модели на примере плоской задачи двумерной упругости прямоугольной лопатки, подверженной воздействию центробежных сил F постоянной интенсивности. Плоскость лопатки жестко заделана в основании (рисунок 5.1). В последующем эту модель можно применить как для других плоских задач НДС, так и для построения более сложных моделей тел.

Представление конечных элементов упругими эквивалентными моделями необходимо для точного определения соотношения деформаций и усилий внутри элемента. Механическую модель элемента будем строить из условия ее эквивалентности квадратному образцу из такого же материала и с такими же размерами по результатам испытания на растяжение- сжатие. Лопатку (рисунок 1) мысленно раздели на n интервалов перпендикулярно ее сторонам. Индекс i соответствует сечениям, перпендикулярным заделке лопатки, индекс j-сечением, параллельным заделке. Из числа n² квадратных элементов шириной а и толщиной листа h выделим один с i-м нижним и j-м левым сечением. Этот элемент представим в виде механической модели (рисунок 5.2), состоящей из осевых пружин 1 жесткости C₁

Рисунок 5.1 – Схема расчленения лопатки, подверженной воздействию центробежных сил, на элементы.

и контурных пружин 2 жесткости С₂ наклоненных к осевым линиям под углом 45⁰ .Концы пружин соединены шарнирами А, В, С, Д. Этими шарнирами данный элемент (его контуры обведены штриховыми линиями) соединяются с другими элементами. Отброшенные элементы по аксиоме связей заменяются векторами нормальных сил ( 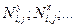) и векторами касательных сил ( ).

Коэффициенты жесткости пружин С₁ и С₂ определим из условия жесткости данного образца при одноосном нагружении, например по оси y, силой P_y. Деформация образца , по осям У и Х ( рис.5.2) соответственно определяются по закону Гука:

(5.1)

Где Е – модуль упругости Юнга, -коэффициент Пуассона. Вырежем узлы А и В сечениями 1-1 и II-II , и из решения их уравнений равновесия найдем формулы для определения С₁ и С₂

(5.2)

Перемещения шарниров А, В, С, Д по отношению к центу элемента в направлении их нормальных усилий обозначим соответственно 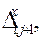(рисунок 5.2). Эти перемещения определяются из уравнений равновесия при вырезании шарниров по сечениям 1- 1,..., IV-IV в проекциях на нормальные оси. Для сокращения изложения алгоритм исследования напряженно-деформированного состояния приведет в дальнейшем для упрощенного варианта данной модели , когда оси элемента АС и ВД остаются ортогональными друг к другу и осевые пружины жестко соединены в точке их пересечения в процессе деформирования.

Уравнения равновесия представим в матричной форме.

, (5.3)

где вектор искомых перемещений и вектор нормальных условий элемента выражаются матрицами столбцами:

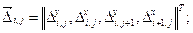(5.4)

Квадратная матрица 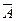определяется коэффициентами жесткости С_1, С₂

(5.5)

Где С₁₂= С₁ + С₂.

Решение системы уравнений можно представить в виде

(5.6)

Рисунок 5.2- Механическая модель элемента расчленения твердого тела в виде шарниров, соединенных структурными, дискретными, упругими связями.

Уравнение (5.6) представляют собой усовершенствованную форму физических уравнений, полученных на основе закона Гука.

В таблице 5.1 представлены пять результатов решения системы четырех уравнений (5.3) по определению в зависимости от вариантов заданных сил в шарнирах А, В, С, Д. Рассматривался элемент с модулем ( ) размерами: а= 16.66 мм; h=1мм. Полученные значения перемещений согласуются с законом Гука .

Для повышения точности моделирования предполагается задать модели с возможностью угловых деформаций стержней, что увеличит число уравнений. Однако представленная модель определяет соотношение силовых факторов и продольных деформаций двумерной упругости для одного элемента, а в их совокупности определит и угловые деформации.

Замена данными моделями упругого континиума соответствует зернисто – кристаллическому строению металлов. Упругие модели, представляющие отдельные зерна металла с анизотропной кристаллической структурой, стыкуются по границам зерен, имеющим разрывы межатомных силовых связях по отдельным направлениям.

Таблица 5.1- Результаты решения системы уравнений для элемента по определению в зависимости от вариантов заданных сил в шарнирах А,В,С,Д.

Номер варианта		Шарниры
А	Б	С	Д
	2.778 ∙10-3	-0.8337∙ 10-3	2.778 ∙10-3	-0.8337∙10-3
	2.6537∙ 10-3	-0.4169 ∙10-3	0.125 ∙10-3	0.4169 ∙10-3
	1.945∙ 10-3	1.945∙ 10-3	1.945 ∙10-3	1.945 ∙10-3
			-1000		-1000
	3.613 ∙10-3	3.613∙10-3	3.613∙ 10-3	3.613 ∙10-3
	2.362∙ 10-3	1.819 ∙10-3	2.362 ∙10-3	-0,708 ∙10-3