Свойства сходящихся числовых последовательностей.

Последовательность { x _n } называется ограниченной снизу ( сверху ), если существует такое число C , что все члены последовательности удовлетворяют условию x _n ≥ C ( x _n ≤ C ). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.

Не всякая ограниченная последовательность является сходящейся. Примером расходящейся ограниченной последовательности может служить последовательность { x _n }: x _n = (–1) ⁿ .

Теорема о трех последовательностях. Если последовательности {x_n}, {y_n}, {z_n} таковы, что x_n ≤ y_n ≤ z_n для всех n ≥ N, и

то последовательность {y_n} сходится, и

Если и для любого то a ≥ b.

Свойства сходящихся последовательностей:

Основные свойства сходящихся последовательностей

1. Если все элементы бесконечно малой последовательности {х_n} равны одному и тому же числу с, то с = 0.

2. Сходящаяся последовательность имеет только один предел.

3. Сходящаяся последовательность ограничена.

4. Сумма (разность) сходящихся последовательностей {х_n} и {у_n} есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательностей {х_n} и {у_n}.

5. Произведение сходящихся последовательностей {х_n} и {у_n} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {х_n} и {у_n}

6. Частное двух сходящихся последовательностей {х_n} и {у_n} при условии, что предел последовательности {у_n}отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {х_n} и {у_n}.

7. Если элементы сходящейся последовательности {х_n} удовлетворяют неравенству x_n ≥ b (х_n ≤ b) начиная с некоторого номера, то и предел а этой последовательности удовлетворяет неравенству а ≥ b (а ≤ b).

8. Произведение бесконечно малой последовательности на ограниченную последовательность или на число есть бесконечно малая последовательность.

9. Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

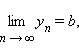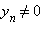Справедлива следующая теорема (основная теорема теории пределов): если то: ; ; при условии, что b ≠ 0 и для всех n.

Последовательность {α_n} называется бесконечно малой, если

Если число a – предел последовательности {x_n}, то последовательность {α_n}, где α_n = x_n – a, бесконечно малая. Примером бесконечно малой последовательности является геометрическая прогрессия {qⁿ}, где |q| < 1.

• Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
• Из определения бесконечно малой последовательности непосредственно следует, что алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что конечность числа бесконечно малых последовательностей в этой алгебраической сумме существенна.
• Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что и здесь конечность числа последовательностей также существенна, т. к. произведение бесконечного числа бесконечно малых последовательностей может уже и не быть бесконечно малой последовательностью.

Множества и называются δ-окрестностями –∞ и +∞ соответственно.

Последовательность {x_n} называется бесконечно большой, если

Другими словами, , если для любого δ > 0 найдется номер такой, что для любого Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {n²} или {1 – n}.

Пример 3. Найти предел .

Решение. При числитель и знаменатель дроби стремятся к бесконечности, т.е. применить сразу теорему о пределе частного нельзя, так как она предполагает существование конечных пределов последовательностей. Преобразуем данную последовательность, разделив числитель и знаменатель на n2. Применяя затем теоремы о пределе частного, пределе суммы и снова пределе частного, последовательно находим