Свойства определенного интеграла

1. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. , где х, t – любые буквы.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.

3. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.

4. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

5. Постоянный множитель можно выносить за знак определенного интеграла.

6. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

Теорема о среднем.Определенный интеграл от функции , непрерывной на отрезке [a, b], равен значению подынтегральной функции в некоторой «средней» точке с промежутка интегрирования, умноженному на длину этого промежутка: .

Доказательство. По свойству функций, непрерывных на отрезке достигает своего наименьшего и наибольшего значений и принимает все промежуточные значения между и : . В силу того, что , предположив, что a<b , имеем

Обозначим тогда . По свойству непрерывных функций найдется значение такое, что , Следовательно, из равенства

получим

Замечание.В выражении (14) 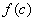называют средним (средним интегральным) значением функции на отрезке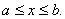

Геометрический смысл среднего значения показан на рис. 6. Значение должно быть таким, чтобы площадь прямоугольника равнялась площади криволинейной трапеции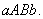

Заметим, что теорема говорит о существовании точки , но не дает способа ее нахождения.

Свойства непрерывных функций на отрезке.

Функция называется непрерывной на отрезке , если она непрерывна во всех точках интервала , непрерывна справа в точке и непрерывна слева в точке . Функции, непрерывные на отрезке, обладают рядом замечательных свойств.

Теорема 1. Если функция непрерывна на отрезке , то она ограничена на нем, т. е. существует константа такая, что выполняется неравенство .

На рисунке изображен график непрерывной функции на отрезке . Очевидно, существует число такое, что находится ниже прямой , но выше прямой В этом и заключается теорема 1.

Заметим, что если функция непрерывна на интервале или на полуинтервале или , то она не обязательно ограничена на нем. Например, функция непрерывна на полуинтервале , но не ограничена на нем.

Если эту функцию доопределить, положив , то она будет конечной в любой точке отрезка , однако, не ограниченной на нем.

Доказательство. Допустим, что не ограничена на . Тогда для каждого натурального числа найдется точка такая, что

. (1)

Последовательность ограничена ( и - конечные), и из нее можно выделить подпоследовательность , сходящуюся к некоторому числу . Но в точке функция непрерывна (если 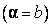, то в этой точке непрерывна справа (слева)), и потому

. (2)

Свойство (2) противоречит свойству (1). Поэтому может быть только ограниченной на .

Теорема 2 (Вейерштрасса). Если функция непрерывна на , то существует ее минимум и максимум на , т. е. существуют точки такие, что для всех . Иначе говоря .

Непрерывная функция 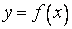достигает своего минимума на в точке и максимума в точке . В данном случае обе точки и принадлежат к интервалу . Непрерывная функция 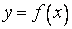, изображенная на рис. 26, достигает минимума на отрезке на левом его конце и максимума - в некоторой внутренней точке этого отрезка.

Замечание 1. По теореме 1 непрерывная на отрезке функция ограничена на нем. Следовательно, существуют конечные точные нижняя и верхняя грани на этом отрезке:

.

Теорема 2 утверждает, что эти грани на достигаются, т. е. здесь и можно заменить соответственно на и (минимум и максимум).

Рис. 26 Рис. 27

Доказательство

По предыдущей теореме непрерывная на функция ограничена, следовательно, она ограничена сверху некоторым числом :

. Но тогда существует точная верхняя грань на :

. (3)

Число 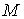обладает следующим свойством: для любого натурального числа найдется на точка такая, что .

Последовательность , как принадлежащая к , ограничена, и потому из нее можно выделить подпоследовательность , сходящуюся к некоторому числу , которое заведомо принадлежит . Но функция непрерывна в точке , и потому

С другой стороны, .

Но так как может стремиться только к одному пределу, то . Верхняя грань (3), таким образом, достигается в точке , т. е., как говорят, функция достигает в точке своего максимума на отрезке . Мы доказали, что существует точка , для которой

.

Доказательство другой части теоремы о минимуме аналогично, но его можно свести к доказательству первой части теоремы, учитывая, что

.

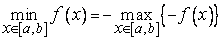Теорема 3. Если функция непрерывна на отрезке и числа и не равны нулю и имеют разные знаки, то на интервале имеется по крайней мере одна точка такая, что .

Функция, график которой изображен на рис. 27, удовлетворяет условиям теоремы 3. Она непрерывна на и , . Из геометрических соображений очевидно, что график должен пересечь ось по крайней мере в одной точке . Это и утверждает теорема 3.

Доказательство

Обозначим отрезок через . Разделим на две равные части. Если в середине функция равна нулю, то теорема доказана; если этого нет, то одна из половинок такова, что на концах ее наша функция принимает значения разных знаков. Обозначим именно эту половинку через и разделим ее на две равные части. Может случиться, что в середине наша функция равна нулю, и тогда теорема доказана. Если нет, то обозначим через ту из половинок, на концах которой принимает значения разных знаков. Рассуждая так по индукции, мы либо наткнемся на очередном этапе рассуждений на точку , для которой , и тогда теорема доказана, либо получим последовательность (бесконечную) вложенных друг в друга отрезков , на каждом из которых имеет значения разных знаков. Тогда существует точка , принадлежащая всем , следовательно, и . Очевидно, , потому что, если допустить, например, что 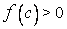, то нашлась бы окрестность точки такая, что для всех из , принадлежащих , функция 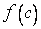была бы положительной, но этого не может быть, потому что при достаточно большом отрезок , а не сохраняет знак на . Теорема доказана.

Следствие. Если функция непрерывна на , и - произвольное число, находящееся между числами и , то на интервале найдется по крайней мере одна точка , для которой .

Это следствие можно сформулировать и так: непрерывная на отрезке функция принимает все промежуточные значения между ее значениями на концах отрезка .

БЛОК