
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Однородные сферические монохроматические волны
Сферической волной называют любое решение волнового уравнения (1.14) вида
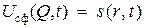 , (1.34)
, (1.34)
где  . Иначе говоря, в случае сферической волны величина
. Иначе говоря, в случае сферической волны величина  в каждый момент времени постоянна на сфере
в каждый момент времени постоянна на сфере  . Общее решение (1.34), выражающее сферическую волну, расходящуюся от начала координат, имеет вид
. Общее решение (1.34), выражающее сферическую волну, расходящуюся от начала координат, имеет вид
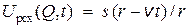 .
.
Множитель  выражает закон сохранения энергии при распространении сферической волны и учитывает, что интенсивность сферической волны
выражает закон сохранения энергии при распространении сферической волны и учитывает, что интенсивность сферической волны
 (1.35)
(1.35)
остается постоянной в процессе распространения. Здесь  — площадь поверхности сферы, а
— площадь поверхности сферы, а  – символ пропорциональности.
– символ пропорциональности.
Скалярное комплексное выражение для электрического поля сферической расходящейся монохроматической волны получается из (1.17) в результате замены t на  , так что с учетом однородности
, так что с учетом однородности  имеем
имеем

Откуда комплексная амплитуда однородной сферической расходящейсямонохроматической волны
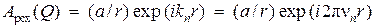 . (1.36)
. (1.36)
Так как общее выражение для сферической волны, сходящейся к началу координат, имеет вид
 ,
,
то комплексно сопряженная амплитуда
 (1.37)
(1.37)
соответствует однородной сферической сходящейсямонохроматической волне.
Сравнение выражений (1.29)и (1.36)показывает, что плоская и сферическая волны локально похожи друг на друга. В самом деле, на достаточно большом расстоянии от начала координат в некоторой малой окрестности можно приближенно считать, что, например, векторы  и
и  коллинеарны, так что
коллинеарны, так что  . Это и означает локальное совпадение комплексных амплитуд
. Это и означает локальное совпадение комплексных амплитуд  и
и 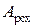 .
.
В окрестности некоторой оси, например  , сферическую волну удобно рассматривать в параксиальном приближении. В этом случае величину r в знаменателе (1.36)можно приближенно заменить на
, сферическую волну удобно рассматривать в параксиальном приближении. В этом случае величину r в знаменателе (1.36)можно приближенно заменить на  , а в фазовом множителе разложить по биному
, а в фазовом множителе разложить по биному

Тогда для комплексной амплитуды имеем

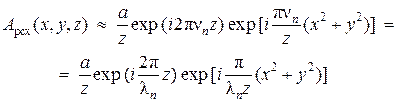 (1.38)
(1.38)
Таким образом, в параксиальном (квадратичном)приближении сферическая волна аппроксимируется параболической волной.
Однородная сферическая монохроматическая волна, так же как и плоская волна, является типовым оптическим сигналом СП. Центральная, осевая и плоскостная симметрия сферической волны соответствуют изотропности СП. При этом описание множества S входных сигналов набором сферических волн приводит к построению пространственно-координатной ВншМП СП.
Модельное представление линейной ОиЛзЭС
Внешняя линейная МП ОиЛзЭС
Всоответствии с (1.6)идентифицируем поведение ОиЛзЭСс помощью формально заданного оператора PОиЛзЭСосуществляющего преобразование множества S={s} входных оптических сигналов во множество Σ={σ}выходных (преобразованных)оптических или электрических сигналов. Явный вид оператора поведения PОиЛзЭСопределяется в каждом случае в рамках выбранной ВнтрСМ с учетом МП структурных ПЭ иклассов входных ивыходных сигналов. Воптических системах входные ивыходные сигналы могут быть вещественными (интенсивность)иликомплексными (амплитуда поля)функциями пространственных координат, времени идлины волны. Вэлектронных системах они представляют собой вещественные функции одной независимой переменной (времени), для описания которых также используется понятие комплексного сигнала.
Основной задачей ВншСМ является описание внешней структурной связности ОиЛзЭС как «черного ящика» в результате выделения типовых входных и выходных сигналов, согласованных о пространственно-временной симметрией ОиЛзЭС, и построения классов сигналов связности RS и RΣ. Так как учет внешних параметров  влияет прежде всего на конкретную МП, то без ограничения общности преобразующие свойства ВншСМ (1.6)пятимерной ОиЛзЭС, которая является отправной моделью для построения всех вариантов ММ ОиЛзЭС, описываются выражением
влияет прежде всего на конкретную МП, то без ограничения общности преобразующие свойства ВншСМ (1.6)пятимерной ОиЛзЭС, которая является отправной моделью для построения всех вариантов ММ ОиЛзЭС, описываются выражением
 PОиЛзЭС
PОиЛзЭС  (1.39)
(1.39)
где х, у, z – входные; x', y', z' – выходные независимые пространственные переменные; λ – длина волны; t – время.
В случае произвольной ОС пространственные переменные рассматриваются как координаты в пространстве предметов и пространстве изображений.
Одним из основных внешних свойств СМ является линейная структурная связность  входных и
входных и  выходных сигналов, задаваемая подмножествами в виде линейных комбинаций некоторых типовых сигналов
выходных сигналов, задаваемая подмножествами в виде линейных комбинаций некоторых типовых сигналов

 (1.40)
(1.40)
где  вообще говоря, комплексные коэффициенты. В результате выражение (1.6) с учетом (1.40) представляет собой линейно связную ВншСМ ОиЛзЭС.Более того, линейно связное представление сигналов (1.40) позволяет значительно упростить математическое описание ППС в ОиЛзЭС и конкретизировать вид МП (1.11), вводя в рассмотрение ОиЛзЭС с линейным поведением.
вообще говоря, комплексные коэффициенты. В результате выражение (1.6) с учетом (1.40) представляет собой линейно связную ВншСМ ОиЛзЭС.Более того, линейно связное представление сигналов (1.40) позволяет значительно упростить математическое описание ППС в ОиЛзЭС и конкретизировать вид МП (1.11), вводя в рассмотрение ОиЛзЭС с линейным поведением.
В общем случае ОиЛзЭС называют линейной (ЛОиЛзЭС),если ее поведение описывается линейным преобразующим оператором Pлоэс,который линейную комбинацию входных сигналов преобразует в линейную комбинацию выходных сигналов, так что
 (1.41)
(1.41)
Говорят, что ЛОиЛзЭС удовлетворяет принципу суперпозиции и переводит входную линейную связность  в преобразованную линейную связность
в преобразованную линейную связность  , так что
, так что  . Соответствующую внешнюю линейную МП (ВншЛМП)ОиЛзЭС или любого ее ПЭ b с учетом (1.11) можно представить в виде
. Соответствующую внешнюю линейную МП (ВншЛМП)ОиЛзЭС или любого ее ПЭ b с учетом (1.11) можно представить в виде
 . (1.42)
. (1.42)
Она лежит в основе общей теории линейных систем, в которых результат воздействия линейной комбинации входных сигналов носит аддитивный характер. Основное преимущество линейных систем состоит втом, что ихреакцию (отклик) на какой-либо сложный сигнал можно выразить через отклики на некоторые «элементарные» типовые входные сигналы, каждый из которых вызывает отклик известного вида [11,21,26,28].
Базисные типовые сигналы
На практике большинство оптических систем обладает осевой симметрией, обусловленной осевой симметрией зеркально-линзовых оптических ПЭ иизотропностью СП.Элементарным объектом излучения с осевой симметрией является точечный источник, 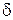 -МП которого имеет следующий вид
-МП которого имеет следующий вид
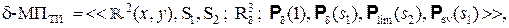
где 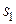 –распределения яркости L (x, у)иликомплексной амплитуды А (х,у);
–распределения яркости L (x, у)иликомплексной амплитуды А (х,у);  –δ-образная аппроксимирующая последовательность
–δ-образная аппроксимирующая последовательность  [см. (П.5.4)];
[см. (П.5.4)];  –тернарное
–тернарное 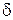 -отношение, задаваемое формулой (П.5.1); Pδ(1):
-отношение, задаваемое формулой (П.5.1); Pδ(1):  [см. (П. 5.2)]; Pδ(
[см. (П. 5.2)]; Pδ( 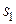 ) :
) :  [см. (П.5.10)] – операторы поведения δ-функции; Plim(s2) :
[см. (П.5.10)] – операторы поведения δ-функции; Plim(s2) :  [см. (П.5.4)] – аппроксимация δ-функции; Psv (s1) :
[см. (П.5.4)] – аппроксимация δ-функции; Psv (s1) :  [см. (П.5.12)] – фильтрующее свойство δ-функции. Поэтому одним из основных типовых сигналов является δ-функция, осевая симметрия которой согласована с осевой симметрией произвольной ОС. Используя фильтрующее свойство δ-МП, входной сигнал
[см. (П.5.12)] – фильтрующее свойство δ-функции. Поэтому одним из основных типовых сигналов является δ-функция, осевая симметрия которой согласована с осевой симметрией произвольной ОС. Используя фильтрующее свойство δ-МП, входной сигнал  можно представить в виде непрерывной линейной комбинации смещенных точечных источников, так что
можно представить в виде непрерывной линейной комбинации смещенных точечных источников, так что
 (1.43)
(1.43)
где  - переменные интегрирования в предметной плоскости х у;множитель
- переменные интегрирования в предметной плоскости х у;множитель  служит амплитудным коэффициентом, с которым суммируются δ-функции. С оптико-физической точки зрения (1.43) можно рассматривать как непрерывную двумерную сумму точечных источников
служит амплитудным коэффициентом, с которым суммируются δ-функции. С оптико-физической точки зрения (1.43) можно рассматривать как непрерывную двумерную сумму точечных источников  с амплитудой
с амплитудой  ,локализованных в фиксированных точках
,локализованных в фиксированных точках 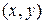 предметной плоскости
предметной плоскости  (рис. П.З). Так как выражение (1.43) справедливо для любого сигнала, то континуальный набор
(рис. П.З). Так как выражение (1.43) справедливо для любого сигнала, то континуальный набор  смещенных δ-функций образует базис в пространствах входных S и выходных Σ сигналов, а сами δ-функции называют базисными типовыми δ-сигналами в координатном представлении. Таким образом (1.43) задает связность
смещенных δ-функций образует базис в пространствах входных S и выходных Σ сигналов, а сами δ-функции называют базисными типовыми δ-сигналами в координатном представлении. Таким образом (1.43) задает связность  в виде непрерывной линейной δ-связности в классах входных и выходных сигналов путем упорядочения подмножества точечных источников и лежит в основе координатного (пространственно-координатного и координатно-временного) подхода к описанию ППС в ОиЛзЭС.
в виде непрерывной линейной δ-связности в классах входных и выходных сигналов путем упорядочения подмножества точечных источников и лежит в основе координатного (пространственно-координатного и координатно-временного) подхода к описанию ППС в ОиЛзЭС.
Каждый точечный источник  предметной плоскости формирует сферическую расходящуюся волну, и, наоборот, каждая точка
предметной плоскости формирует сферическую расходящуюся волну, и, наоборот, каждая точка  идеального геометрооптического изображения получается с помощью сходящейся сферической волны (рис. 1.6). Поэтому в СП базисные типовые сигналыпринимают вид сферических волн (1.36) и (1.37). Разложение комплексной амплитуды поля по этим волнам задается линейным оператором СП (2.13) в виде двумерной непрерывной суммы расходящихся сферических волн (2.14).
идеального геометрооптического изображения получается с помощью сходящейся сферической волны (рис. 1.6). Поэтому в СП базисные типовые сигналыпринимают вид сферических волн (1.36) и (1.37). Разложение комплексной амплитуды поля по этим волнам задается линейным оператором СП (2.13) в виде двумерной непрерывной суммы расходящихся сферических волн (2.14).
Высококорригированные оптические изображающие системы (ОИзС) с малым угловым полем формируют изображение одинакового качества в пределах всего линейного поля. Иначе говоря, они обладают симметрией сдвига, когда смещение объекта излучения приводит к соответствующему смещению изображения без изменения его качества. При этом симметрия сдвига ОИзС обусловлена не только высокой степенью коррекции объектива, но и однородностью СП. Симметрия сдвига присуща всем периодическим излучающим объектам и идентифицируется с разложением таких сигналов в тригонометрический ряд Фурье (П.2.1) или (П.2.2). Поэтому элементарным объектом излучения, обладающим симметрией сдвига, является гармоническая пространственно-частотная решетка (транспарант). Для представления непериодических сигналов в виде непрерывной линейной комбинации гармоник используется вещественный интеграл Фурье (П.3.1) с учетом (П.3.2) и (П.З.З). Тогда одним из основных типовых сигналовявляются также косинусоидальная  или синусоидальная
или синусоидальная  гармоники, задающие поведение элементарного оптического периодического объекта, симметрия сдвига которого на пространственный период
гармоники, задающие поведение элементарного оптического периодического объекта, симметрия сдвига которого на пространственный период 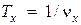 соответствует симметрии сдвига оптической изображающей и фурье-преобразующей системы.
соответствует симметрии сдвига оптической изображающей и фурье-преобразующей системы.
В силу практической универсальности разложения сигнала в дискретную или непрерывную сумму гармоник с определенной амплитудой и фазой соответствующий набор гармоник образует базис в пространстве сигналов. Поэтому сами косинусоидальные  и синусоидальные
и синусоидальные  гармоники называют базисными типовыми сигналами в частотном представлении(базисными пространственно-частотными или частотно-временными гармониками).
гармоники называют базисными типовыми сигналами в частотном представлении(базисными пространственно-частотными или частотно-временными гармониками).
При этом в основе разложения сигнала по базисным частотным гармоникам лежит гармонический анализ сигналов (прил. 2 и 3). Таким образом, представление сигнала рядом или интегралом Фурье задает гармоническую линейную  связностьв классах входных и выходных сигналов путем выделения упорядоченного подмножества гармоник и лежит в основе частотного подходак пространственно-временному описанию ППС в ОиЛзЭС.
связностьв классах входных и выходных сигналов путем выделения упорядоченного подмножества гармоник и лежит в основе частотного подходак пространственно-временному описанию ППС в ОиЛзЭС.
При освещении каждой двумерной гармонической решетки плоской нормально падающей волной на ее выходе формируются две плоские волны, дифрагирующие симметрично относительно оптической оси. Верно и обратное, каждые две плоские волны, симметрично падающие на плоскость наблюдения, образуют косинусоидальное или синусоидальное распределение амплитуды [см. (П.2.8) и (П.2.9)]. Таким образом, в СП пространственно-частотные базисные сигналыпринимают вид плоских волн. При этом разложение комплексной амплитуды поля по плоским волнам задается в виде комплексного ряда Фурье (П.2.10) и (П.2.12) или обратного преобразования Фурье (П.3.12) и (П.3.15).
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...