
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Статистическая оценка измеряемых параметров сигнала
5.7.1. Задача измерения параметров сигнала при наличии помех
В самом общем виде задача статистической оценки параметров сигналов (т.е. задача измерения параметров сигналов при наличии помех) может быть сформулирована следующим образом.
Поступающая на вход электронного тракта измерительной ОиЛзЭС реализация представляет собой некоторую комбинацию полезного сигнала  и помехи П(t). Полезный сигнал является детерминированной функцией своих аргументов, среди которых n неизвестных параметров
и помехи П(t). Полезный сигнал является детерминированной функцией своих аргументов, среди которых n неизвестных параметров  (i = 1, 2, …, n), подлежащих измерению (существенных параметров), m неизвестных параметров
(i = 1, 2, …, n), подлежащих измерению (существенных параметров), m неизвестных параметров  (j = 1, 2, …, m), в оценке значений которых нет необходимости (несущественных параметров), и q известных параметров
(j = 1, 2, …, m), в оценке значений которых нет необходимости (несущественных параметров), и q известных параметров  (k = 1, 2, …, q). Каждый из неизвестных параметров является непрерывной или дискретной случайной величиной, имеющей некоторый закон распределения. В течение времени наблюдения (времени измерения [
(k = 1, 2, …, q). Каждый из неизвестных параметров является непрерывной или дискретной случайной величиной, имеющей некоторый закон распределения. В течение времени наблюдения (времени измерения [  ,
,  ]) оцениваемые параметры
]) оцениваемые параметры  могут изменяться. Априорная вероятность присутствия полезного сигнала в реализации равна единице
могут изменяться. Априорная вероятность присутствия полезного сигнала в реализации равна единице  , так как режим обнаружения завершен и объект находится в поле зрения ОиЛзЭС.
, так как режим обнаружения завершен и объект находится в поле зрения ОиЛзЭС.
В таких условиях на основе соответствующего анализа принятой реализации ОиЛзЭС должна решить вопрос, какие значения имели существенные параметры  сигнала на интервале наблюдения [
сигнала на интервале наблюдения [  ,
,  ]. Поскольку из-за наличия случайной помехи точное измерение произвести невозможно, процесс измерения носит вероятностный характер – характер статистических оценок.
]. Поскольку из-за наличия случайной помехи точное измерение произвести невозможно, процесс измерения носит вероятностный характер – характер статистических оценок.
Существует два вида таких оценок: интервальная (доверительная) оценка и точечная оценка. В первом случае должен быть определен тот интервал, в пределах которого с заданной вероятностью находится истинное значение измеряемого параметра. Эта вероятность называется доверительной вероятностью или коэффициентом доверия, а сам интервал – доверительным интервалом.
При точечной оценке измерительная ОиЛзЭС выдает некоторое число (оценку) 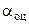 , которое характеризует с заданной достоверностью истинное значение измеряемого параметра
, которое характеризует с заданной достоверностью истинное значение измеряемого параметра 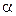 . Поскольку оценка
. Поскольку оценка  является случайной величиной, то в качестве меры достоверности используется статистическая характеристика (например, среднеквадратическое отклонение
является случайной величиной, то в качестве меры достоверности используется статистическая характеристика (например, среднеквадратическое отклонение  оценки
оценки  от истинного значения параметра
от истинного значения параметра 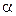 , где ).
, где ).
Теория статистических оценок позволяет с той или иной степенью приближения решить задачу в рассмотренной наиболее общей постановке. Установлено, например, что для сигналов, измеряемые параметры которых на интервале времени наблюдения [  ,
,  ] изменяются, наилучшие результаты получены при нелинейной обработке входной реализации [19]. Оптимальная линейная фильтрация может быть реализована лишь в тех случаях, когда указанным изменением практически можно пренебречь.
] изменяются, наилучшие результаты получены при нелинейной обработке входной реализации [19]. Оптимальная линейная фильтрация может быть реализована лишь в тех случаях, когда указанным изменением практически можно пренебречь.
В дальнейшем будем предполагать, что форма полезного сигнала известна и он содержит лишь один неизвестный параметр  (амплитуду, фазу, частоту, длительность и т. д.), который необходимо измерить. Сигнал полностью расположен внутри интервала наблюдения, на границах которого как сам сигнал, так и его производные равны нулю.
(амплитуду, фазу, частоту, длительность и т. д.), который необходимо измерить. Сигнал полностью расположен внутри интервала наблюдения, на границах которого как сам сигнал, так и его производные равны нулю.
Поскольку оцениваемый параметр a является значением непрерывной или дискретной случайной величины  , то наиболее полным описанием, с помощью которого можно получить представление о возможных значениях этого параметра, является функция
, то наиболее полным описанием, с помощью которого можно получить представление о возможных значениях этого параметра, является функция  , представляющая собой апостериорную условной плотность вероятности параметра
, представляющая собой апостериорную условной плотность вероятности параметра  при условии получения реализации s. Действительно, если бы на основе соответствующей обработки входной реализации удалось получить функцию
при условии получения реализации s. Действительно, если бы на основе соответствующей обработки входной реализации удалось получить функцию  (рис. 5.16а), то естественно в качестве оценки измеряемого параметра принять его наиболее вероятное значение
(рис. 5.16а), то естественно в качестве оценки измеряемого параметра принять его наиболее вероятное значение 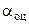 , соответствующее Кр 1° (Котельникова) максимума апостериорной условной вероятности
, соответствующее Кр 1° (Котельникова) максимума апостериорной условной вероятности  или
или  (см. рис. 5.16а). Причем если функция имеет не один, а несколько максимумов, то оценкой должно являться (рис. 5.16б) значение параметра, соответствующее наибольшему максимуму (верхней грани).
(см. рис. 5.16а). Причем если функция имеет не один, а несколько максимумов, то оценкой должно являться (рис. 5.16б) значение параметра, соответствующее наибольшему максимуму (верхней грани).
5.7.2. Нахождение 
Формула для совместной плотности вероятности  аналогична по структуре выражению (5.2) для вероятности совместного появления двух событий:
аналогична по структуре выражению (5.2) для вероятности совместного появления двух событий:
 . (*)
. (*)
Откуда  , (**)
, (**)
где  - полная априорная плотность вероятности измеряемого параметра
- полная априорная плотность вероятности измеряемого параметра  ;
; 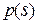 - полная априорная плотность вероятности получения реализации
- полная априорная плотность вероятности получения реализации 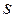 ;
;  - найденная на эксперименте условная апостериорная плотность вероятности получения реализации
- найденная на эксперименте условная апостериорная плотность вероятности получения реализации 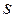 при условии, что измеряемый параметр имеет значение
при условии, что измеряемый параметр имеет значение 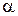 . При этом
. При этом  , рассматриваемая как функция
, рассматриваемая как функция 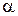 , называется функцией правдоподобия (см. п. 5.2, стр. 284) и имеет два значения
, называется функцией правдоподобия (см. п. 5.2, стр. 284) и имеет два значения 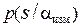 и
и  .
.
1) В случае дискретной обработки входной реализации 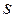 плотности вероятности
плотности вероятности 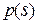 и
и  являются N-мерными плотностями, где N – объем выборки. 2) При непрерывной обработке эти плотности вероятности бесконечномерны и могут рассматриваться как пределы N-мерных плотностей при N → ∞.
являются N-мерными плотностями, где N – объем выборки. 2) При непрерывной обработке эти плотности вероятности бесконечномерны и могут рассматриваться как пределы N-мерных плотностей при N → ∞.
Аналогично характер функции  зависит от вида априорного распределения
зависит от вида априорного распределения  измеряемого параметра a. Поскольку
измеряемого параметра a. Поскольку
 , (5.69')
, (5.69')
где  - область возможных значений параметра
- область возможных значений параметра 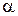 . Далее (5.69') с учетом (**) можно представить в виде
. Далее (5.69') с учетом (**) можно представить в виде
 , (***)
, (***)
Откуда  . (5.70)
. (5.70)
Подставляя (5.70) в формулу (**), получим
 . (****)
. (****)
Таким образом, для нахождения искомой апостериорной условной плотности вероятности  измеряемого параметра
измеряемого параметра  необходимо знать 1) априорную плотность
необходимо знать 1) априорную плотность  и 2) с помощью принятой реализации
и 2) с помощью принятой реализации 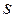 найти функцию
найти функцию  .
.
1) Как и при решении задач обнаружения, априорная информация  может отсутствовать. Тогда в отношении функции
может отсутствовать. Тогда в отношении функции  должна быть принята некоторая гипотеза, которая соответствует наихудшим условиям измерений и гарантирует получение более качественных результатов при всех других видах априорного распределения. Иначе говоря, при оценке неизвестных параметров сигналов так же, как и при обнаружении сигналов может применяться Кр 3° максимума правдоподобия, или минимаксный критерий. В этом случае не требуется знания априорной вероятности
должна быть принята некоторая гипотеза, которая соответствует наихудшим условиям измерений и гарантирует получение более качественных результатов при всех других видах априорного распределения. Иначе говоря, при оценке неизвестных параметров сигналов так же, как и при обнаружении сигналов может применяться Кр 3° максимума правдоподобия, или минимаксный критерий. В этом случае не требуется знания априорной вероятности  .
.
2) Что касается функции правдоподобия  , то её определение представляет серьезные трудности. Выходом является переход к отношению правдоподобия. Поскольку
, то её определение представляет серьезные трудности. Выходом является переход к отношению правдоподобия. Поскольку
 , (5.71)
, (5.71)
то подставляя из (5.71)  =
= 
 в (****), получим
в (****), получим
 =
=
 (5.72)
(5.72)
В результате для получения искомой апостериорной условной плотности вероятности  измеряемого параметра
измеряемого параметра 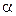 достаточно извлечь из принятой реализации отношение правдоподобия, т. е. вначале решения в режиме обнаружения и оценки параметров сигнала с этой точки зрения совпадают. Однако в дальнейшем процессы формирования решения различны. В ОиЛзЭС обнаружения отношение правдоподобия сравнивается с его пороговым значением (п. 5.2).
достаточно извлечь из принятой реализации отношение правдоподобия, т. е. вначале решения в режиме обнаружения и оценки параметров сигнала с этой точки зрения совпадают. Однако в дальнейшем процессы формирования решения различны. В ОиЛзЭС обнаружения отношение правдоподобия сравнивается с его пороговым значением (п. 5.2).
В измерительной ОиЛзЭС использующей, например, правило оценки по Кр 1° максимума апостериорной условной вероятности, необходимо, используя (5.72), найти функцию  и получить значение параметра
и получить значение параметра 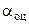 , которому соответствует верхняя грань этой функции (рис. 5.16).
, которому соответствует верхняя грань этой функции (рис. 5.16).
При решении задачи измерения параметров сигналов, помимо Кр 1° максимума апостериорной условной вероятности, используются и другие критерии, сходные с критериями обнаружения. Однако прежде чем перейти к описанию правил формирования оценок, рассмотрим общие положения по анализу эффективности этих правил.
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...