Функция потерь, линейная по модулю

Подставляя (5.74) в (5.79) при линейной по модулю функции потерь для апостериорного условного риска имеем

Тогда уравнение (5.80) для отыскания байесовской оценки 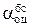принимает вид

Откуда

, (7)

и, следовательно, байесовская оценка 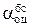соответствует тому значению измеряемого параметра 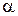, при котором площади Ë(D₁) и Ë(D₂) областей и под кривой апостериорной плотности вероятности 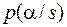слева и справа равны (рис. 5.19). Иначе говоря, оценка 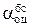есть медиана апостериорного распределения 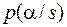измеряемого параметра.

Подставляя (5.74) при в (5.78), получим безусловный средний риск

, (8)

т.е. байесовский риск при линейной по модулю функции потерь равен минимальному среднему отклонению байесовской оценки от истинного значения параметра.

Квадратичная функция потерь

Для квадратичной функции потерь из (5.79) и (5.75) следует

,

так что условие (5.80) для нахождения байесовской оценки имеет вид

Откуда с учетом получим

. (9)

Таким образом, байесовская оценка при квадратичной функции потерь равна среднему значению по апостериорной плотности распределения измеряемого параметра. Из (5.78) и (5.75) получим соответствующий байесовский риск (безусловный средний риск), который минимизирует

(10)

Он равен минимальному среднему значению квадрата отклонения оценки 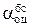от истинного значения 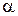измеряемого параметра, т.е. дисперсии байесовской погрешности.

Прямоугольная функция потерь

При прямоугольной функции потерь из (5.79) и (5.76) имеем

(5.81)

В итоге получаем уравнение для нахождения оценки 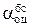в виде

или

. (11)

Откуда следует (рис. 5.20), что байесовская оценка при прямоугольной функции потерь равна такому значению параметра 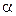, при котором апостериорные плотности вероятности, соответствующие значениям и , равны между собой.

Второй член в формуле (5.81) определяет вероятность появления события, заключающего в том, что истинное значение параметра в данной реализации находится в диапазоне от до . Следовательно, в соответствии с этой же формулой апостериорный условный риск 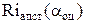при прямоугольной функции потерь равен вероятности того, что истинное значение параметра 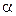не находится в этом диапазоне, т.е.

Байесовский риск

т.е. определяет минимальную вероятность того, что погрешность выйдет за пределы диапазона .

5.8.4. Выводы

На основании изложенного для нахождения оценки неизвестного параметра 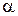сигнала необходимо:

1. В зависимости от характера решаемой задачи, определяющей связь между погрешностью измерения и вызываемыми ею последствиями (т.е. её «стоимостью»), выбрать соответствующую функцию потерь .

2. Подвергнуть принятую реализацию 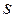такой обработке, при которой можно получить:

2.1. Отношение правдоподобия 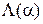, если функция потерь суть 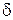-равномерная, а априорное распределение измеряемого параметра можно считать равномерным;

2.2. Апостериорную условную плотность вероятности 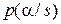измеряемого параметра при всех остальных функциях потерь; а также при 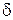-равномерной функции потерь, если известно, что априорное распределение отличается от равномерного.

3. В соответствии с выбранной функцией потерь провести анализ функци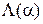й или , на базе которого найти оценку неизвестного параметра, являющуюся наилучшей (оптимальной в некотором смысле) оценкой.

Критерий оптимальности оценки также зависит от выбранной функции потерь .

3.1. При 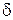-равномерной функции потерь работает критериймаксимума апостериорной вероятности (Кр. 1°); или (если априорное распределение измеряемого параметра равномерное) критерий максимума правдоподобия (Кр. 3°). В обоих случаях измерительная ОиЛзЭС, работающая по этим критериям, обеспечивает максимальную вероятность правильной оценки, т.е. максимальную вероятность того, что оценка 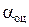совпадает с истинным значением параметра .

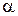3.2.При линейной по модулю функции потерь байесовская оценка дает возможность получить минимум математического ожидания (среднего значения) погрешности .

3.3. При квадратичной функции потерь байесовская оценка 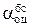идентифицирует минимум среднеквадратического отклонения оценки от истинного значения измеряемого параметра, т.е. минимизирует дисперсию погрешности .

3.4. При прямоугольной функции потерь байесовская оценка 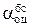идентифицирует минимальную вероятность выхода погрешности измерения за границы поля допуска .

4. Вообще говоря, байесовские оценки при линейной, квадратичной и прямоугольной функции потерь не совпадают друг с другом, а также с при 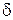-равномерной функции потерь, т.е. с оценкой по максимуму апостериорной вероятности [см. рис. 5.18 (стр. 335а), 5.19 (стр. 336а) и 5.20 (стр. 337а)]. Совпадение всех оценок возможно, лишь тогда, когда апостериорное распределение 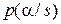унимодально и симметрично (рис. 5.18, стр. 335а).

При линейной обработке входной реализации , т.е. при получении линейных оценок достаточно, чтобы помеха имела нормальное распределение. При других видах распределения помехи или при нелинейной обработке входной реализации требуется идентификация апостериорной условной плотности распределения вероятности измеряемого параметра при заданной измерительной ОиЛзЭС.