Разложение функции в степенные ряды

Математическое введение

Разложение функции в степенные ряды

Любую непрерывную функцию y = f(x) можно разложить в ряд по степеням (x-a) в окрестности точки а (ряд Тэйлора). Ряд имеет следующий вид:

f(x) = f(a) + f ’(a)*(x-a) + 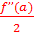*(x-a)² + …

у

х

а

Геометрический смысл разложения в ряд. Оставим вначале лишь первую степень. Если мы оставим так, то это аппроксимация функции линейной зависимости. Если мы оставляем и вторую степень в разложении, то мы аппроксимируем функцию параболы, имеющую тот же наклон и ту же выпуклость. Это более точная аппроксимация, чем прямой.

Примеры разложения некоторых функций.

y = ln(1+x)

u – полезность.

c – потребление

функция полезности человека.

y = ln(1+x)

y’ = (ln(1+x))’

u’(V(x) = u’(V)* V’(x)

y’ =

y’’ = ( )’ = -(1+x) ^-2 = -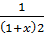

ln(1+x) = x – ½ * x²

ln (1+x) = x – x²/2

При малых х, получается ln(1+x) = x. Разложение функции в ряд эффективно в малых окрестностях точки.

Соответствующая функция полезности имеет вид:

u = ln (1 + W/W₀)

W – богатство.

Второй пример. экспоненциальная функция полезности.

е^х

е^-х

-е^-х

u = 1 – e ^–W/Wo

Разложим функцию в ряд.

y =e^-x

y’ = -e^-x

y’’ = - (e^-x)’ = e^x

f(x) = 1 – x + ½ x²

y = e^x = 1 – x + x²/2

y = 1 – e^-x = 1 – (1 – x + x²/2) = x – x²/2

При малых х получим, что e^x = 1 + x

Третья модельная функция.

y = x^α

(x+a)^α – a^α

u(W) = (W+Wo) ^α– Wo ^α

y = (x+a)^α – a^α

y’ = (x+a)^α-1 = α*a ^α-1

y’’ = α*(α-1)*(x+a)^α-2 = α(α-1)* a^α-2

y = α*a^α-1 * x + (α(α-1)* a^α-2 )/2 * x² = α+a^α-1 * (x+ (α-1/2a) * x²)

Самая простая модельная функция полезность – квадратичная.

W₀² – (W – W₀)² , W<W₀

Замечание. Поскольку имеют значение лишь предельные полезность, постоянные слагаемые в полезности можно не писать.

W₀² – (W – W₀)² , 1 – e ^–W/Wo, (W+Wo) ^α– Wo ^α , ln (1 + W/W₀)

В формуле степенной функции полезности Wo иногда не пишут.

Замечание о правдоподобности модели полезности. Квадратичная модель мало похожа на реальность, т.к. предельная полезность изменяется с изломом

u’ = - 2(W-Wo) = Wo-W.

Экспоненциальная модель полезности означает насыщение полезности и очень сильное избегание риска

u’ = 1/Wo * e ^–W/Wo .

Наиболее реальной считается степенная модель полезности. Предельным случаем её является логарифмическая при α стремящейся к 0

u‘ = 1/ (1+W/Wo) * 1/Wo = 1/ Wo + W.

Операции статистического усреднения.

Допустим х – случайная величина. Она характеризуется статистическими параметрами – статистическими моментами.

Первый момент: математическое ожидание или среднее значение (х или <x> или Е(х))

х = х₁р₁ + х₂р₂ + …

Второй момент: х² = х₁ ²р₁ + х₂ ²р₂ + …

Второй центральный момент: (х - х)² – дисперсия. Это средний квадрат случайных колебаний вокруг ожидаемого значения.

Стандартное отклонение или мера риска: Ổ = √ (х – х)

Для двух случайных величин рассматривают смешенные вторые моменты:

<x*y> = х₁*у₁*р₁ + х₂*у₂*р₂ + … - второй смешенный момент.

Второй смешенный центрированный момент: Bxy = <(x – x)*(y – y)> - ковариация.

Другие представления дисперсии и ковариации:

Ổх² = (х – х)² = х² – 2х*х + х = х² – х² – дисперсия

Bxy = <(x – x)*(y – y)> = <x*y –x*y – x*y + x*y > = <x*y> - x*y

<xy> = Bxy + x*y

Ковариация легко поддается расчету, однако не является наглядной величиной. Более наглядной считается корреляция.

Рху = Bxy / (Ổx*Ổy)

Корреляция P может быть в пределах от -1 до 1. Корреляция считается мерой статистической связи. Когда от 0 до 1, то статистическая связь положительная. Когда от -1 до 0, то преимущественно величины изменяются в противоположных направлениях.

Тема. Основа теории полезности

Полезность – микроэкономическая категория, которая характеризует субъективную оценку привлекательности определенного блага или события с точки зрения конкретного индивидуума. Полезность позволяет описать выбор с точки зрения конкретного потребителя. Полезность конкретного товара или набора потребления можно выразить с помощью индивидуальной функции полезности, которая характеризует зависимость полезности от количества потребляемого товара.

U - полезность

Количество товара

Поведение рациональных потребителей подчиняется закону убывающей предельной полезности, которая предполагает, что каждая следующая единица потребляемого товара приносит меньшую полезность, чем предыдущая. Предельная полезность (MU) – дополнительная полезность, которая приносит потребителю единицы потребляемого товара.

MU = ∆U / ∆количество товара = U’

Микроэкономический выбор между различными вариантами потребления описывается с помощью кривой безразличия. Кривая безразличия – кривая соединяющая различные варианты потребления приносящую одинаковую полезность

дрова Рв = 5, Рд = 2, W = 10

2 Валенки

Выбор потребителя осуществляется при совмещении кривых безразличия с бюджетным ограничением, учитывающим доступные средства и цены товаров. При фиксированном уровне цен набор потребляемых товаров, при определенном уровне дохода, будет конкретным и будет приносить конкретную полезность. На основе этого можно построить функцию полезности доходов.

богатство

При этом для рационального потребителя будет справедливо убывающая предельная полезность дохода. Вследствие этого закона потери воспринимаются потребителем чувствительней, чем соответствующее приобретен.

Гипотеза ожидаемой полезности

В соответствии с данной гипотезой в условиях риска индивидуумы действуют таким образом, чтобы максимизировать ожидаемую полезность своего потребления. При этом ожидаемая полезность – средневзвешенная по вероятности полезность различных возможных исходов.

EU = ΣPi*Ui*Wi

Примерчик. Инвестор может получить рискованный доход 1000 рублей с вероятностью 1/2 или гарантированный доход 300 рублей. Какой вариант для него более предпочтительный.

Решение:

Вариант 1: W = 300

U(300)

Вариант 2: W = 1000 p = ½

W = 0 p = ½

U = ½ U(1000)+1/2U(0) = 1/2U(1000)

Инвестор выберет второй вариант.

Убывающая предельная полезность дохода предполагает, что рациональные потребители являются избегающими риска. Это означает, что безрисковый доход они ценят выше, чем рискованный с таким же ожидаемым значением.

Примерчик. Имеется возможность получить доход 900 рублей с вероятностью 1/3 или безрисковый доход 300 рублей.

Решение.

U(300) > 1/3U(900)

U

W

300 900

В случае если инвестор безразличен к риску рискованные и безрисковые доходы он будет рассматривать как одинаково привлекательные, а азартный инвестор (расположенный к риску) будет предпочитать рискованный доход.

Безрисковый рисковый

В реальной экономической ситуации большинство инвесторов являются избегающими риска.

Модельные функции полезности.

Модельные функции математически описывают поведение рациональных инвесторов избегающих риска. Они используются для упрощения реальных экономических задач.

Квадратическая функция полезности.

U(W) = C² – (W – C)²

C – индивидуальный параметр избегания риска конкретным инвестором.

U’(W) = 2(C – W)

2C

C

Логарифмическая функция.

U(W) = ln(1+W/C)

U’(W) = 1/ (1+W/C) * 1/C

Экспоненциальная функция

U(W) = 1 – e ^–W/C

U’(W) = 1/C * e ^–W/C

Степенная функция.

U(W) = W^α , 0<α>1

U’(W) = α*W ^α-1

Задачи!!!!!!!!!!!!!!!!!!!

Гипотеза ожидаемой полезности Неймона-Моргенштерн.

Ф.Найт в 1921 году. Самостоятельно прочитать про него: Найт «риск и неопределенность».

u = p₁u₁ + p₂u₂ …

Основы теории оценивания активов.

Тобин, конец 1950

Шарп,1964. CAPM – первая версия теории оценивания

Блэк, Шоуз1973

Как охватить финансовые активы картиной полезности? Основная функция финансовых активов перераспределять потребления между периодами времени.

t t+1

Поэтому, чтоб охватить картину финансовой полезности нужно рассматривать многопериодную функцию полезности.

U (C_t, C_t+1,…)

Принимается следующая модель полезности

U (C_t, C_t+1,…) = u(Ct) + Ɣ< u(C_t+1)> (1) - базованя модель полезности

Ɣ = 1 означало бы, что потребителю все равно иметь ли сейчас или в следующем периоде.

Ɣ= ½, означает, что благо сейчас приносит вдвое больше удволитворения чем в следующем периоде.

Ɣ = 0 означает, что потребление потом не имеет значение.

Все что, связано с будущим периодом, связано с риском.

Pt – на момент t

Ct – за определенный момент.

Вывод формулы справедливой цены актива.

В каком случае индивид будет относиться к покупке актива безразлично? Предположим в момент t мы покупаем немного акций. pt – цена одной акции в начальный момент. Пусть xt+1 – момент дохода продажи акций в момент t/ Тогда U_новое = u(Ct - pt∆₰) + Ɣ <u(C_t+1 + xt+1∆₰)>

Справедливая цена будет такой при которой производная U’(∆₰) = 0.

u’(ct - pt∆₰) = (-pt) + Ɣ <u’(C_t+1 + x_t+1∆₰)*x_t+1>

поскольку мы ищем производную вблизи состояния равновесия то можно пренебречь pt∆₰ и x_t+1∆₰.

u’(ct)(-pt) = Ɣ <u’(C_t+1)*x_t+1>

pt = ₰ * (<u’(Ct+1)*xt+1> / u’(ct)) (2)– формула цены.

Экономический смысл формулы цены: зависимость от ₰. Если ₰ уменьшается, цены активов падают.

Чем больше ожидаемая будущая продажная цена акции (x_t+1) тем текущая цена выше.

Чем богаче рассчитывает быть потребитель в будущем тем ниже текущая цена акций. активы оцениваются на фоне предполагаемого будущего потребления индивида.

pt = ₰ * (<u’(C_t+1)*x_t+1> / u’(ct)) = ₰{u(C_t+1*x_t+1 + B_u’x}/ u’(Ct)

К чему приводит статистическая связь будущего благосостояния и будущей цены активов. Предположим C_t+1 и x_t+1 изменяются связанно с положительной корреляцией. Такое обычно характерно для большинства акций. U’(C_t+1) x_t+1. Для таких активов корреляция будет отрицательна. Для большинства ценных бумаг корреляция будет отрицательна. Эта статистическая связь будет снижать цену. Это снижение цены объясняются тем, что люди избегают риска. Активы, работающие противоположным образом – это например страховки.

Переход к описанию в терминах ожидаемой доходности. Для дальнейшего введем обозначение mt₊₁ = ₰U’(C_t+1)/ U’(Ct) – субъективный фактор дисконтирования. Тогда формулу цены можно переписать так:

p_t = <m_t+1*x_t+1> ( 2’)

Хотя формула 2 и 2’ имеет прозрачный экономический смысл, проверить их на опыте не представляется возможным, поскольку x_t+1 никогда не известно. Поэтому, от описания в терминах цены переходят к описанию в терминах ожидаемой доходности, т.к. появляется возможность проверить модель на опыте. Пусть R_t+1 = x_t+1/Pt = 1+r_t+1 – валовая доходность. p_t = <x_t+1>/<R_t+1>. <R_t+1> - дисконт, с которым оценивается актив по отношению к своей предполагающей будущей цене.

Например. Если в будущем мы хотим получить 1000 с доходностью 20% , то мы должны вложить 100/1,2 = 883. Смысл формул: не прирост, а дисконт.

Прежде всего разделим формулу 2’ на текущую цену. Получим:

1 = <m_t+1*R_t+1>. Воспользуемся формулой . Получается: 1 = В*(mt+1*Rt+1) + <mt+1>*<Rt+1>. Рассмотрим оценивание безрискового актива. Получим: p_t = <m_t+1>*x_t+1 Разделим на Pt. Получим: 1 = <m_t+1>*x_t+1/Pt Получим:

<m_t+1> = 1/Rt. (3)

Подставим: 1 = В*(m_t+1*R_t+1) + 1/Rt*<R_t+1> Далее помножим все на Rf. Получим: Rf = Rf*В*(m_t+1*R_t+1) + <R_t+1> Получаем:

<Rf > = Rf – Rf*B(m_t+1*R_t+1) (4)

Экономический смысл: дисконт, с которым оценивается актив получается суммой 2х слагаемых: безрисковой доходности (Rf) и премией за риск (Rf*B(m_t+1*R_t+1)). Эта премия за риск определяется ковариацией будущей доходности актива с фактором дисконтирования. Поэтому, для большинства обычных ценных бумаг ковариация будет отрицательна и премия за риск оказывается положительной (задача 2.1).

Дисконтирование – изменение ценности денег со временем в отсутствии риска, обязано во первых тому, что люди нетерпеливы, Ɣ<1 и во вторых – в среднем люди ожидают роста благосостояния. Изменение ценности денег во времени иногда называют эффектом процентной ставки. В его основе лежит экономический рост. И все это без учета риска.

Построение кривых безразличия

Построение кривых безразличия позволяют инвестору сформулировать свои цели связанные с построением портфеля. Выбирая инвестиционный портфель инвестор стремиться выбрать такой набор активов, который обеспечивает ему максимально ожидаемую полезность из доступных вариантов.

<u(w_T)> стремиться к максимуму

w_T = w_o(1+r_p)

<u(w₀+w₀*r_p)> стремиться к максимуму

Поскольку предполагается, что срок инвестирования небольшой и получаемая за этот период доходность близка к 0 можно разложить данную функцию в степенной ряд вблизи доходности равной 0.

r_p = 0

f(x) = f(a) + f’(a)(x-a) + f’’(a)/2! * (x-a)² + …

<u(w0+w0*rp)> = <u(w0+w0*0)> + <u’(w0+w0*0)*(rp-0)*w0> + <u’’(w0+w0*0)w0² * (rp-0)²/ 2!> = max

<u(w_T)> = u(w₀) + u’(w₀)*w₀*<r_p>*u’’(w₀)*w₀²/2 * <r_p²> = max

<u(w_T)> = u’(w₀)*w₀*(r_p + u’’(w₀)*w₀/2u’(w0) *< rp²>) = max

<u(w_T)> = r_p + u’’(w₀)*w₀/2u’(w0) *< rp²> = max

Отношение к риску конкретного инвестора измеряется с помощью 2х показателей:

1) Коэффициент относительного избегания риска показывает на какое увеличение риска согласен инвестор при увеличении доходности на 1 %

φ = - u’’(w₀)*w₀ / u’(w₀)

2) Коэффициент толерантности к риску показывает какое увеличение доходности требует инвестор при увеличении риска на 1%.

ι = 2/φ = - 2u’’(w0)*w0 / u’(w0)

Вторая производная функции полезности всегда будет отрицательной величиной в следствии закона убывающей предельной полезности, поэтому перед выражениями стоит знак минус, чтобы коэффициенты были положительными.

rp = φ/ι *<r_p²> = max

rp = <r_p>/ι = max

Ổ_rp² = <r_p²> - r_p²

<r_p²> = Ổ_rp² + r_p²

rp = Ổ_rp² + r_p²/ι = max

поскольку доходность портфеля близка к 0 квадрат этой величины будет ещё меньше и при оптимизации структуры портфеля ей можно пренебречь.

<u> = r_p - Ổ_rp²/ι = max - функция полезности марковеца.

В теория выбора портфеля Марковеца выбор структуры инвестиций происходит на основе максимизации данного выражения. При этом инвестор стремиться увеличивать ожидаемую доходность портфеля (поскольку это увеличивает ожидаемую полезность) и стремиться минимизировать риск (поскольку он снижает ожидаемую полезность).

Все портфели лежащие на одной кривой безразличия приносит инвестору одинаковый уровень ожидаемой полезности и являются для него одинаково ценными несмотря на то, что имеют разные инвестиционные характеристики.

<u(A)> = <u(B)>

r_p^a = 20%

Ổ_rp^a = 25%

r_p^B = 30%

Ổ_rp^B = 33.5%

<u(A)> = 0.2 – 0.252/0.5 = 0.075

<u(B)> = 0.3 – 0.3352/0.5 = 0.075

Конкретный инвестор имеющий конкретное отношение к риску оценивает 2 портфеля лежащие на одной кривой безразличия одинаково и не может из них выбрать. Портфели лежащие на разных кривых безразличия имеют разный уровень привлекательности для инвестора. Чем на более высокой кривой лежит портфель, тем выше его полезность.

Формируя инвестиционный портфель инвестор стремится выбрать из доступных вариантов такой, который лежит на самой высокой кривой безразличия и обеспечивает наибольшую ожидаемую полезность. Кривые безразличия конкретного инвестора зависят от его толерантности к риску. Чем сильнее инвестор избегает риска, тем больше будет наклон кривых безразличия. Избегающий риска инвестор за небольшое увеличение риска требует большое увеличение доходности для того, чтобы портфель приносил такую же полезность, а агрессивный инвестор за небольшое увеличение доходности готов согласиться на большое увеличение риска. Отношение инвестора к риску измеряется коэффициентом толерантности и относительным избеганием риска.

<u> = 0

0 = ∆rp - Ổp² / ι

Толерантность характеризует, какое увеличение дисперсии инвестор согласен принимать при увеличении доходности на 1%.

Коэффициент относительного избегания риска показывает на сколько должна увеличиться доходность портфеля при изменении дисперсии на 1. Толерантность и избегание риска зависят от первоначального богатства инвестора и от характеристик его функций полезности.

Содержание уравнения CML

Линейное эффективное множество, рассматриваемое всеми инвесторами и представляющее собой сочетание рыночного портфеля с безрисковыми активами называется линией рынка капитала (CML).

CML

Характеристики любого эффективного портфеля лежащего на CML могут быть описаны в виде уравнения прямых.

y = a + b*x

a = y(0)

a = r_f

b = y₁-y₀ / x₁-x₀

b = r_M – rf / Ổm

rp = r_f + (r_M – rf / Ổm)*Ổp - уравнение CML

Уравнение CML описывает ожидаемую доходность любого портфеля являющегося эффективным. Все другие портфели, которые можно сформировать на рынке будут лежать ниже CML. Уравнение CML показывает, что ожидаемая доходность эффективного портфеля зависит от риска этого портфеля прямой линейной зависимостью. Ожидаемая доходность портфеля, являющегося эффективным зависит от следующих параметров:

1) Безрисковая доходность (чем больше доходность безрисковых инвестиций, тем больше результат он хочет получать от рискованных вложений)

2) Среднерыночная премия за единицу риска (r_M – rf / Ổm ). Чем большая доходность требуется на рынке в целом тем больше требуемая доходность конкретного портфеля.

3) Риск конкретного эффективного портфеля.

u’(c_t+1) = u’(st + st*r^p_t+1) = u’(st) + u’’(st)* st * r^p_t+1 = u’(st)*(1+u’’(st)/u’(st) * st * r^p_t+1 = u’(st)*(1- (-u)’’(st)/u’(st) * st * r^p_t+1 = u’(st)*(1-φ* r^p_t+1)

Тогда фактор дисконтирования: mt+1 = Ɣu’(st)/u’(ct) *(1-φ* r^p_t+1)

m_t+1 = G*(1-φ* r^p_t+1)

Дисконт будет тем больше, чем больше доходность портфеля и чем больше избегание риска.

B(Rt+1, mt+1) = <(R_t+1 – R_t+1)(m_t+1 – m_t+1)>

mt+1 = G*(1-φ* r^p_t+1)

m_t+1 – m_t+1 = -G*φ(r^p_t+1 – r^p_t+1)

m_t+1 – m_t+1 = -G*φ(R^p_t+1 – R^p_t+1)

B(Rt+1, mt+1) = <(R_t+1 – R_t+1)(m_t+1 – m_t+1)> =-Gφ <(R_t+1 – R_t+1)*(R^p_t+1 – R^p_t+1) > = -G*φ*B(Rt+1,R^p_t+1)

<R_t+1> = R_f + R_f *G* φ*B(Rt+1,R^p_t+1)

Выразим безрисковую доходность в портфельном приближении

Rf = 1/m_t+1 = 1/G*(1-φ* r^p_t+1)

<R_t+1> = R_f + G*φ/ G*(1-φ* r^p_t+1) – B(R_t+1, R^p_t+1)

<R_t+1> = R_f + φ/ (1-φ* r^p_t+1) – B(R_t+1, R^p_t+1)

В портфельном приближении пренебрегают (1-φ* r^p_t+1)

<Rt+1> = R_f+φ*B*(R_t+1, R^p_t+1) – уравнение оценивания в портфельном приближении

Премия за риск зависит от:

1) Ковариации доходности актива с портфелем (Ổ*Ổp*Ῥip)

2) Степени избегания риска инвестором (φ)

Проблема межвременного выбора

С оцениванием активов тесно связана проблема межвременного выбора. Какую часть богатства индивид будет стремиться направить на потребление, а какую на сбережение, вкладывая в активы. Описать выбор между потреблением и сбережением.

u(ct) + Ɣ<u((w₀ - c_t)R_t+1)>

u’(ct) - Ɣ<u’((w₀ - c_t)R_t+1)*R_t+1> = 0

задача 3.1.

w0 = 6000

Rf = 1.08

Ɣ = 0.98

u(c) = ln(1+c / c)

решение.

u’(c) = 1/ c+c

1/c+ct – Ɣ * Rf/c + (w0-ct)*Rf

Математическое введение

Разложение функции в степенные ряды

Любую непрерывную функцию y = f(x) можно разложить в ряд по степеням (x-a) в окрестности точки а (ряд Тэйлора). Ряд имеет следующий вид:

f(x) = f(a) + f ’(a)*(x-a) + 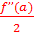*(x-a)² + …

у

х

а

Геометрический смысл разложения в ряд. Оставим вначале лишь первую степень. Если мы оставим так, то это аппроксимация функции линейной зависимости. Если мы оставляем и вторую степень в разложении, то мы аппроксимируем функцию параболы, имеющую тот же наклон и ту же выпуклость. Это более точная аппроксимация, чем прямой.

Примеры разложения некоторых функций.

y = ln(1+x)

u – полезность.

c – потребление

функция полезности человека.

y = ln(1+x)

y’ = (ln(1+x))’

u’(V(x) = u’(V)* V’(x)

y’ =

y’’ = ( )’ = -(1+x) ^-2 = -

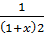
ln(1+x) = x – ½ * x²

ln (1+x) = x – x²/2

При малых х, получается ln(1+x) = x. Разложение функции в ряд эффективно в малых окрестностях точки.

Соответствующая функция полезности имеет вид:

u = ln (1 + W/W₀)

W – богатство.

Второй пример. экспоненциальная функция полезности.

е^х

е^-х

-е^-х

u = 1 – e ^–W/Wo

Разложим функцию в ряд.

y =e^-x

y’ = -e^-x

y’’ = - (e^-x)’ = e^x

f(x) = 1 – x + ½ x²

y = e^x = 1 – x + x²/2

y = 1 – e^-x = 1 – (1 – x + x²/2) = x – x²/2

При малых х получим, что e^x = 1 + x

Третья модельная функция.

y = x^α

(x+a)^α – a^α

u(W) = (W+Wo) ^α– Wo ^α

y = (x+a)^α – a^α

y’ = (x+a)^α-1 = α*a ^α-1

y’’ = α*(α-1)*(x+a)^α-2 = α(α-1)* a^α-2

y = α*a^α-1 * x + (α(α-1)* a^α-2 )/2 * x² = α+a^α-1 * (x+ (α-1/2a) * x²)

Самая простая модельная функция полезность – квадратичная.

W₀² – (W – W₀)² , W<W₀

Замечание. Поскольку имеют значение лишь предельные полезность, постоянные слагаемые в полезности можно не писать.

W₀² – (W – W₀)² , 1 – e ^–W/Wo, (W+Wo) ^α– Wo ^α , ln (1 + W/W₀)

В формуле степенной функции полезности Wo иногда не пишут.

Замечание о правдоподобности модели полезности. Квадратичная модель мало похожа на реальность, т.к. предельная полезность изменяется с изломом

u’ = - 2(W-Wo) = Wo-W.

Экспоненциальная модель полезности означает насыщение полезности и очень сильное избегание риска

u’ = 1/Wo * e ^–W/Wo .

Наиболее реальной считается степенная модель полезности. Предельным случаем её является логарифмическая при α стремящейся к 0

u‘ = 1/ (1+W/Wo) * 1/Wo = 1/ Wo + W.