метод. Метод двойного предпочтения

Если таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем.

В каждом столбце отмечают знаком V клетку с наименьшей стоимостью. Затем то же проделывают в каждой строке. В результате некоторые клетки имеют отметку VV. В них находится минимальная стоимость, как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая из рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по ячейкам, отмеченным знаком V. В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.

Пример 2.6.3

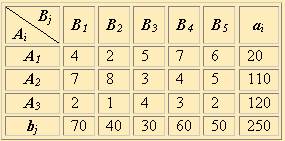
Применим метод двойного предпочтения к задаче, условия которой записаны в табл. 2.8.

Таблица 2.8

Сначала, отмечаем знаком V ячейку с наименьшей стоимостью в каждом столбце, затем - в каждой строке (табл. 2.9).

Таблица 2.9

Ячейки A1B4 , A2B1 , A3B5 имеют отметку VV, следовательно, с них и начинаем заполнение. Затем заполняем ячейку A4B2 (т.к. в столбце B2 нет ни одной ячейки с отметкой VV). В оставшейся части таблицы последовательно заполняем ячейки по минимальной стоимости A1B3 , A4B3 , A4B5 . План, полученный в табл. 2.10, является вырожденным опорным планом.

Таблица 2.10

Вычислим общую сумму затрат на перевозку груза по этому плану:

Z = 100*1 + 200*2 + 50*10 + 200*2 + 200*8 + 50*12 + 50*13 = 4250 (ед.).

Таким образом, наименьшую стоимость имеет опорный план, полученный методом двойного предпочтения, следовательно, он наиболее близок к оптимальному плану.

Упражнения

Составить опорные планы различными методами, сравнить значения суммарной стоимости перевозок по каждому плану.

1.

2.

3.

4.

Открытые модели ТЗ и усложнения в ее постановке

Транспортная задача, в которой суммарные запасы и потребности совпадают, т. е. выполняется условие называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая:

а) суммарные запасы превышают суммарные потребности: ;

б) суммарные потребности превышают суммарные запасы: .

Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.

Открытая модель ТЗ решается приведением к закрытой модели. В случае (а), когда суммарные запасы превышают суммарные потребности, т.е. , вводится фиктивный потребитель (столбец Вn+1), потребности которого . В случае (б), когда суммарные потребности превышают суммарные запасы, т.е. , вводится фиктивный поставщик (строка Am+1), запасы которого .

Стоимость перевозки единицы груза, как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится.

После преобразований задача принимает вид закрытой модели и решается обычным способом. При равных стоимостях перевозки единицы груза, от поставщиков к фиктивному потребителю, затраты на перевозку груза реальным потребителям минимальны, а фиктивному потребителю будет направлен груз от наименее выгодных поставщиков. То же самое получаем и в отношении фиктивного поставщика.

Замечание 1. Прежде чем решать какую-нибудь транспортную задачу, необходимо сначала проверять, к какой модели она принадлежит, и только после этого непосредственно составлять распределительную таблицу.

Замечание 2. При составлении первоначального опорного плана методом минимальной стоимости или двойного предпочтения необходимо наименьшую стоимость выбирать только среди стоимостей реальных поставщиков и потребителей, а запасы фиктивного поставщика (потребности фиктивного потребителя) распределять в последнюю очередь. Это позволит получить план, более близкий к оптимальному.

Отмеченное во втором замечании используют также при введении фиктивно запятых клеток.

Рекомендации приведения задачи к обычной ТЗ

При решении конкретных транспортных задач приходится часто учитывать некоторые дополнительные ограничения: невозможность (запрет) поставки груза из Ak в Вi (блокировка), обеспечение пункта Вj , заданным количеством aij единиц груза за счет пункта отправления Ai и т.п. В этих случаях поступают следующим образом:

Запрет перевозок груза из Ai в Вj осуществляется занесением в клетку Ai Вj числа cij = М > 0 (здесь и в последующем М - сколь угодно большое число). При оптимальном плане эта клетка будет блокирована.

По условию задачи требуется доставить из Ai в Вj αij единиц груза. Следует занести в начале заполнения таблицы в клетку Ai Вj число αij , считать ее в дальнейшем свободной (cij = М), а потребности bj и запасы аi уменьшить на αij. Найденный оптимальный план новой задачи будет оптимальным и для исходной (с добавлением xij = αij ).

Если требуется из Ai в Вj завести груз xij ≥ 0 - заданного числа, то уменьшают запасы аi и потребности bj на αij и находят оптимальный план новой задачи, по которому определяют и решение исходной задачи (x*ij = αij + xij, где xij > 0 - компонента плана новой задачи).

Иногда требуется перевезти из Ai в Вj груза не более заданного объема xij < αij. Тогда, чаще всего, поступают следующим образом: в таблицу вводят дополнительный столбец В*j с тарифами, равными тарифам столбца Вj , кроме клетки Ai Вj , где полагают cij = М. При этом потребности пункта Вj считаются равными αij , a В*j - равными bj - αij .

Находят решение полученной задачи обычными методами или устанавливают ее неразрешимость. Заметим, что исходная ТЗ разрешима лишь в том случае, когда для нее существует хотя бы один опорный план.

Пример 2.8.2

Выпуск продукции трех заводов А1 , А2 , А3 составляет соответственно 260, 240 и 300 т. Потребности четырех потребителей В1 , В2 , В3 , В4 равны соответственно 300, 200, 250 и 100 т. Известно, что:

Продукция завода А1 не требуется пункту В4 .

С завода А3 потребителю В2 должно быть доставлено груза не более 50 т.

Стоимость перевозки одной тонны продукции из Аi в Bj задана матрицей

Определить план прикрепления потребителей к заводам, удовлетворяющий поставленным условиям и обеспечивающий минимальные затраты на транспортировку всей продукции завода.

Решение. Заметим, что и поэтому вводим фиктивного поставщика А4 с запасами a4 = 50 и нулевыми тарифами (4-ая строка). Получим закрытую модель ТЗ. Заполняем распределительную таблицу (табл. 2.14) в следующем порядке. В клетку А1 B4 записываем число М (блокируем), тем самым выполнив первое условие задачи. Далее в столбце B2 записываем потребности b2 = 50, остальные b*ij = 150 заносим в дополнительный столбец B*2 . Все тарифы в нем такие же, как и в B2 , лишь в клетке A3 B*2 ставим число М. Далее по принципу минимальной стоимости заполняем клетки таблицы.

Таблица 2.15

Получаем опорный план

X= проверяем его на оптимальность, для чего составляем систему уравнений потенциалов:u1 + v1 = 3, u4 + v3 = 0, Получаем u3 = 0, найдём: v1 = 4, u1 = - 1,

u1 + v2 = 4, u4 + v4 = 0. v2 = 3, u2 = - 4,

u2 + v3 = 2, v3 = 6, u3 = 0,

u3 + v1 = 4, v4 = 6, u4 = - 6.

u3 + v2 = 3,

u3 + v4 = 6,

Проверив свободные клетки, убеждаемся, что для них выполнятся условие (2.23) теоремы 5, следовательно, план X является оптимальным и Zmin = 2680 (ед.).

Пример 2.8.3

По данным примера таблицы 2.16 найти оптимальный план при условии полного обеспечения потребностей пункта В3.

Таблица 2.16

Следуя принципу минимальной стоимости, вносим в клетку А2 В3 груз 240 т. и недостающие 10 т. потребителю B3 заносим из A1. Исключаем из рассмотрения строку A2 и столбец B3 , уменьшая при этом a1 = 260 на 10 т. Решаем новую задачу (табл.2.16)

Таблица 2.17

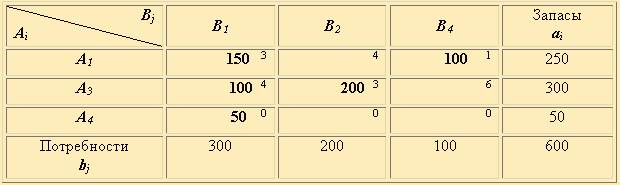
Проверяем оптимальность плана в табл. 2.16 методом потенциалов, и убеждаемся, что все ui+vj < cij в свободных ячейках. Находим Z1 = 1550. Добавив в матрицу, соответствующую последней таблице, строку A2 и столбец B3 из табл.3.18, находим решение задачи

и Zmin = 2090 (ед.).

В основном открытая модель транспортной задачи используется при решении ряда экономических задач.

Упражнения

Решить следующие транспортные задачи с дополнительными условиями (в ячейках таблицы даны тарифы cij, справа от таблицы - запасы ai, внизу ее - потребности bj ).

1.

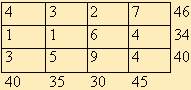
Полностью удовлетворить В2.

Заблокировать клетку А1В4.

2.

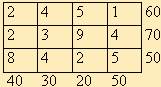
Из А3 в В4 доставить 20 ед. груза.

Вывезти полностью груз из А3.

3.

.

Из А2 в В4 доставить не более 10 ед. груза.

4.

Из А2 в В5 доставить не менее 30 ед.

Пример составления математической модели транспортной задачи

Условие:

Однородный груз сосредоточен у m поставщиков в объемах a1, a2, ... am.

Данный груз необходимо доставить n потребителям в объемах b1, b2 ... bn.

Известны Cij, i=1,2,...m; j=1,2,...n - стоимости перевозки единиц груза от каждого i-го поставщика каждому j-му потребителю.

Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью, и суммарные затраты на перевозку всех грузов являются минимальными.

Исходные данные транспортной задачи записываются в виде таблицы:

Исходные данные задачи могут быть представлены в виде:

вектора А=(a1,a2,...,am) запасов поставщиков

вектора B=(b1,b2,...,bn) запросов потребителей

матрицы стоимостей:

Математическая модель транспортной задачи

Переменными (неизвестными) транспортной задачи являются xij , i=1,2,...,m j=1,2,...,n - объемы перевозок от i-го поставщика каждому j-му потребителю.

Эти переменные могут быть записаны в виде матрицы перевозок:

Так как произведение Cij*Xij определяет затраты на перевозку груза от i-го поставщика j-му потребителю, то суммарные затраты на перевозку всех грузов равны:

По условию задачи требуется обеспечить минимум суммарных затрат.

Следовательно, целевая функция задачи имеет вид:

Система ограничений задачи состоит из двух групп уравнений.

Первая группа из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью и имеет вид:

Вторая группа из n уравнений выражает требование удовлетворить запросы всех n потребителей полностью и имеет вид:

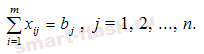
Учитывая условие неотрицательности объемов перевозок математическая модель выглядит следующим образом:

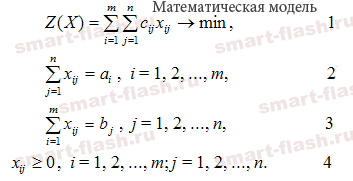
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.:

Такая задача называется задачей с правильным балансом, а модель задачи закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а модель задачи - открытой.

Математическая формулировка транспортной задачи такова: найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений (цифра 2 на математической модели) , (3), условиям неотрицательности (4) и обеспечивающие минимум целевой функции (1)

Пример 34.1

Составить математическую модель транспортной задачи, исходные данные которой приведены в таблице 34.2

Решение:

1. Вводим переменные задачи (матрицу перевозок):

2. Записываем матрицу стоимостей:

3. Целевая функция задачи равняется сумме произведений всех соответствующих элементов матриц C и X.

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

4. Составим систему ограничений задачи.

Сумма всех перевозок, стоящих в первой строке матрицы X, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы X равняться запасам второго поставщика:

Это означает, что запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы X, должны быть равны запросам соответствующих потребителей:

Это означает, что запросы потребителей удовлетворяются полностью.

Необходимо также учитывать, что перевозки не могут быть отрицательными:

Ответ: Таким образом, математическая модель рассматриваемой задачи записывается следующим образом:

Найти переменные задачи, обеспечивающие минимум целевой функции (1) и удовлетворяющие системе ограничений (2) и условиям неотрицательности (3).

Домашнее задание

Вопросы для самоконтроля

1. Сформулируйте математическую постановку транспортной задачи по критерию стоимости перевозок.

2. Опишите структуру распределительной таблицы ТЗ.

3. Сформулируйте математическую модель ТЗ.

4. Какая модель ТЗ называется закрытой, а какая - открытой?

5. Каковы правила приведения открытой модели ТЗ к закрытой?

6. Что называется опорным планом ТЗ?

7. Каковы требования, предъявляемые к опорному плану ТЗ?

8. Что такое цикл и каковы правила его построения в распределительной таблице?

9. Сформулируйте правило «минимального элемента» построения начального опорного плана перевозок.

10. Сформулируйте теорему о потенциалах. Каков её экономический смысл?

11. Опишите алгоритм решения ТЗ методом потенциалов.

12. При каких условиях ТЗ имеет бесконечное множество оптимальных планов перевозок?

13. Как найти всё множество оптимальных планов перевозок ТЗ.

14. Сформулируйте экономическое содержание ТЗ в усложнённой постановке.

15. Сформулируйте экономическое содержание и математическую модель задачи о назначениях.

16. Каковы особенности математической модели задачи о назначениях?

17. Можно ли получить решение задачи о назначениях методом потенциалов?

18. Использование транспортной модели при решении распределительных задач в экономике.