
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Открытая и закрытая модели транспортной задачи
Транспортная задача называется закрытой, если все ее ограничения имеют форму уравнений. В противном случае модель называется открытой. Если бы от каждого поставщика требовалось вывезти всю имеющуюся у него продукцию, ничего не оставляя, а к каждому потребителю было необходимо привезти строго заданное количество продукции, без излишков, то модель была бы закрытой.
 Критерий разрешимости для закрытой модели
Критерий разрешимости для закрытой модели
|
| |

Легко убедиться, что рассмотренный выше пример (задача о холодильных установках) представляет собой открытую модель, и так как 120 + 40 + 90 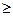 150 + 90 (250
150 + 90 (250 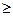 240), она разрешима. Если поставить эту модель, как закрытую, она станет неразрешимой, так как невозможно без излишков поставить 250 холодильных установок в центры сбыта, которые нуждаются всего лишь в 240 установках.
240), она разрешима. Если поставить эту модель, как закрытую, она станет неразрешимой, так как невозможно без излишков поставить 250 холодильных установок в центры сбыта, которые нуждаются всего лишь в 240 установках.
Любую открытую модель можно преобразовать в закрытую.
Если общие запасы превышают потребности (  ), то в модель вводят еще одного потребителя, (m+1)-го по счету. Его принято называть дополнительным или фиктивным. На самом деле его нет, но условно можно считать, что именно к нему свозят все излишки. Соответственно, его «потребность» в продукции bm+1 примем равной
), то в модель вводят еще одного потребителя, (m+1)-го по счету. Его принято называть дополнительным или фиктивным. На самом деле его нет, но условно можно считать, что именно к нему свозят все излишки. Соответственно, его «потребность» в продукции bm+1 примем равной  . Одновременно в модель вводятся n новых переменных xim+1,
. Одновременно в модель вводятся n новых переменных xim+1, 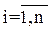 . Каждая из этих переменных по экономическому смыслу представляет собой излишек продукции у i-го поставщика (столько продукции «везут» от i-го поставщика фиктивному потребителю). При этом все новые переменные в целевую функцию не входят (т.е. входят с нулевыми коэффициентами
. Каждая из этих переменных по экономическому смыслу представляет собой излишек продукции у i-го поставщика (столько продукции «везут» от i-го поставщика фиктивному потребителю). При этом все новые переменные в целевую функцию не входят (т.е. входят с нулевыми коэффициентами
cim+1 = 0), поскольку на самом деле перевозки этой продукции не осуществляются. Излишек продукции остается у поставщиков, следовательно, и платить за его перевозку не надо.
Тогда транспортная задача примет вид:
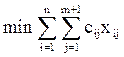
| |

При этом целевая функция в модели (6) может также иметь вид  (отброшенные слагаемые все равно нулевые).
(отброшенные слагаемые все равно нулевые).
Собственно, в зависимости от экономической интерпретации открытой модели критерий ее разрешимости можно и вообще снять. А именно, если общий объем потребностей превышает объем запасов ( 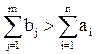 ), можно аналогично ввести дополнительного (фиктивного) поставщика, (n+1)-го по счету. Условно будем считать, что именно у этого поставщика находится вся недостающая продукция, поэтому его запасы
), можно аналогично ввести дополнительного (фиктивного) поставщика, (n+1)-го по счету. Условно будем считать, что именно у этого поставщика находится вся недостающая продукция, поэтому его запасы
аn+1 =  . При этом также придется ввести m новых переменных xn+1j,
. При этом также придется ввести m новых переменных xn+1j,  - это дефицит продукции у j-го потребителя (т.е. та продукция, которую ему «везут» от несуществующего поставщика; этому потребителю ее не хватит). Разумеется, за перевозки несуществующей продукции не платят, поэтому все cn+1j = 0.
- это дефицит продукции у j-го потребителя (т.е. та продукция, которую ему «везут» от несуществующего поставщика; этому потребителю ее не хватит). Разумеется, за перевозки несуществующей продукции не платят, поэтому все cn+1j = 0.
Тогда модель примет вид:
 или
или 
|
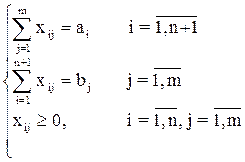
Итак, если в транспортной модели допускается дефицит, то она всегда будет разрешима после преобразования открытой модели в закрытую.
Чтобы преобразовать задачу о холодильных установках в закрытую, необходимо ввести дополнительный (третий) центр сбыта, потребность которого в холодильных установках будет равняться 10 (b3 = 250 - 240 = 10). Одновременно в модель будут введены три новые переменные: x13, х23 и х33 – число установок, не вывезенных соответственно из Стокгольма, Триеста и Руана. В целевую функцию они не войдут (войдут с нулевыми коэффициентами с13 = с23 = с33 = 0) – в самом деле, если установки остаются в центрах производства, затраты на их перевозку не осуществляются. Тогда задача примет вид:
min (25x11 + 14x12 + 18x21 + 8x22 + 12x31 + 6x32)
 x11 + x12 + x13 = 120
x11 + x12 + x13 = 120
x21 + x22 + x23 = 40
x31 + x32 + x33 = 90
x11 + x21+ x31 = 150
x12 + x22+ x32 = 90
x13 + х23 + х33 = 10
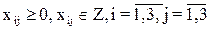
3.4 Задача о распределении специалистов, как пример альтернативной экономической интерпретации транспортной задачи
Рассмотрим пример использования транспортной модели в ситуации, не связанной с перевозкой продукции.
Например, рассмотрим следующую экономическую ситуацию:
Специалистов n различных групп нужно распределить наиболее эффективным образом по m видам работ. Задана матрица эффективности использования специалиста i-й группы на j-м виде работ cij. Кроме того, задано общее количество специалистов каждой группы ai,  и общая потребность в работниках по каждому виду работ bj,
и общая потребность в работниках по каждому виду работ bj,  .
.
Введем переменные хij - количество специалистов i-й группы, занятых на j-м виде работ. Тогда модель строится следующим образом:
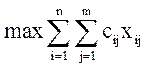
|

Например, НИИ разрабатывает 2 научные программы для молодых ученых, к которым необходимо привлечь соответственно 10 и 7 человек. На участие в них претендуют выпускники аспирантуры 4 учебных заведений, по 5 человек из каждого. Экспертная комиссия пришла к выводу, что эффективность использования одного выпускника каждого учебного заведения в программе № 1 может быть оценена по 5-балльной шкале соответственно в 2, 3, 5 и 1 балл. Для программы № 2 эти оценки составят 3, 1, 5 и 2 балла. Необходимо распределить молодых ученых по научным программам наиболее эффективным образом.
Для построения модели введем переменные xij - количество выпускников i-го учебного заведения, направляемых на j-ю программу. Модель примет вид:
min (2x11 + 3x12 + 3x21 + x22 + 5x31 + 5x32 + x41 + 2x42)
 x11 + x12
x11 + x12  5
5
x21 + x22  5
5
x31 + x32  5
5
x41 + x42  5
5
x11 + x21+ x31 + x41 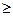 10
10
x12 + x22+ x32 + x42 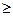 7
7

Задача (8) разрешима при тех же условиях, что и модель (1). Действительно, если общая потребность в работниках не превышает общего числа специалистов, то ее ОДП не пуста (система ограничений здесь такая же, как в модели (1)). Однако целевая функция здесь не минимизируется, а максимизируется. Может ли она быть не ограничена сверху? Нет, не может. Если выбрать в матрице коэффициентов целевой функции самый большой элемент  {cij} и предположить, что каждого специалиста каким-то образом удалось устроить на работу с этой самой большой эффективностью, то мы получим суммарную величину эффективности путем умножения
{cij} и предположить, что каждого специалиста каким-то образом удалось устроить на работу с этой самой большой эффективностью, то мы получим суммарную величину эффективности путем умножения  {cij} на общее число специалистов
{cij} на общее число специалистов  . Значение целевой функции не может быть больше этой величины. В рассмотренном примере самая большая оценка – 5 баллов, а молодых ученых – 20 человек. Следовательно, суммарная эффективность не может превысить 20 * 5 = 100.
. Значение целевой функции не может быть больше этой величины. В рассмотренном примере самая большая оценка – 5 баллов, а молодых ученых – 20 человек. Следовательно, суммарная эффективность не может превысить 20 * 5 = 100.
Взяв коэффициенты целевой функции с противоположным знаком, эту задачу можно поставить на min, и тогда очевидна ее эквивалентность транспортной задаче (1).
Транспортная задача в традиционной интерпретации (о перевозках) также может быть поставлена на максимум. Предположим, что коэффициенты целевой функции cij представляют собой не затраты на перевозку единицы продукции от i-го поставщика к j-му потребителю, а прибыль от реализации единицы продукции i-го поставщика у j-го потребителя. Целью операции будет получение наибольшей прибыли, т.е. max  .
.
Особый класс транспортных задач представляют собой задачи о назначениях*.
3.5 Опорный план транспортной задачи
Метод решения транспортной задачи представляет собой развитие идеи симплекс-метода [3] и тоже основан на переборе опорных планов этой задачи. Опорный план должен включать столько базисных переменных, сколько в задаче линейного программирования независимых уравнений.
Если бы система ограничений закрытой транспортной задачи была линейно независимой, то базисных переменных было бы m+n. Но из задач (6) и (7) видно, что такая система линейных уравнений является линейно зависимой (например, если сложить все ограничения из первой и все из второй группы, а затем вычесть из одной суммы другую, в левой части получится ноль). Можно доказать, что если удалить из системы одно ограничение, то она станет независимой (одно ограничение является лишним, оно следует из остальных). Следовательно, базисных переменных должно быть m+n-1.
Для построения опорного плана транспортной задачи разработано несколько способов, наиболее распространенным является метод северо-западного угла.
3.5.1 Метод северо-западного угла построения опорного плана транспортной задачи
Этот метод принято сокращенно обозначать МСЗУ.
Представим опорный план транспортной задачи в виде таблицы, строки которой будут соответствовать поставщикам (с их запасами ai), столбцы – потребителям (с их потребностями bj), а ячейки – компонентам опорного плана (например, в первой строке первого столбца будет стоять значение переменной x11). Будем заполнять лишь те ячейки, которые будут соответствовать базисным компонентам, переменные в незаполненных ячейках равны нулю.
| x11 | a1 | |||||
| a2 | ||||||
| an | ||||||
| b1 | b2 | bm |
Применение метода начинают с того, что рассматривают левый верхний («северо-западный») угол таблицы, который соответствует переменной x11, т.е. перевозкам от первого поставщика к первому потребителю. Сравнивают их запас и потребность - a1 и b1.
1). Если a1 < b1, то x11 = a1, т.е. всю продукцию первого поставщика отправляют к первому потребителю.
После этого первую строку исключают из рассмотрения (все остальные x1j = 0). В самом деле, ведь запасы первого поставщика уже закончились. Следовательно, больше никому ничего везти от него нельзя.
Первому столбцу вместо b1 ставят в соответствие b1`= b1 - a1, поскольку потребность первого потребителя снизилась (она уже частично удовлетворена).
Затем снова рассматривают левый верхний угол оставшейся части таблицы (без первой строки), т.е. х21.
2). Если a1 > b1 , то x11 = b1., т.е. первого потребителя полностью удовлетворяют за счет запасов первого поставщика, после чего этого потребителя (первый столбец) исключают. Запасы первого поставщика уменьшаются a1`= a1 - b 1.
Затем рассматривают левый верхний угол оставшейся части таблицы (без первого столбца), т.е. х12.
3). Если a1 = b1, то можно исключить либо столбец, либо строку.
Далее действуют аналогично, т.е. либо принимают х21 = min {b1`;a2}, либо принимают х12 = min {b2; a1`}. Процесс продолжается до тех пор, пока не будут исключены из рассмотрения все ячейки. При этом окажется заполненной m+n-1 клетка таблицы.
Рассмотрим применение данного метода к задаче о холодильных установках. Для этого необходимо построить таблицу из трех строк и столбцов, соответствующих шести центрам производства и сбыта (включая дополнительный). Чтобы построить опорный план, необходимо заполнить
3 + 3 – 1 = 5 клеток этой таблицы.
Ее левый верхний угол будет соответствовать поставкам холодильных установок из Стокгольма в Лейпциг (переменной x11). Так как в Стокгольме производится меньше установок, чем необходимо поставить в Лейпциг
(a1 < b1, 120 < 150), то направим все эти 120 установок в Лейпциг (x11 = 120). После этого Стокгольм (первую строку таблицы) можно исключить из рассмотрения, так как холодильных установок в этом центре сбыта больше не осталось. В Лейпциг же необходимо поставить еще 150 – 120 = 30 установок, поэтому Лейпцигу (первый столбец) ставится в соответствие новое значение потребностей – 30:
| Лейпциг | Лион | дополнительный центр сбыта | ||
 Стокгольм Стокгольм
| ||||
| Триест | ||||
| Руан | ||||
| |
Левый верхний угол новой таблицы соответствует поставкам продукции из Триеста в Лейпциг. Так как min{30; 40} = 30, в Лейпциг направляется 30 установок (x21 = 30), после чего потребности Лейпцига удовлетворены полностью, и второй столбец можно исключить из рассмотрения. В Триесте осталось 10 установок:
 |
| Лейпциг | Лион | дополнительный центр сбыта | ||
 Стокгольм Стокгольм
| ||||
| Триест | | |||
| Руан | ||||
| |
Аналогично поставки продукции из Триеста в Лион принимают равными 10 (x22 = 10), а из Руана в Лион – 80 (x32 = 80). После этого в Руане остается еще 10 установок, которые следует перевезти в дополнительный центр сбыта (т.е. потребность в них в рамках данной модели на самом деле отсутствует) - x33 = 10. После этого можно будет исключить из рассмотрения и последний столбец:
 |  | ||
| Лейпциг | Лион | дополнительный центр сбыта | ||
  Стокгольм Стокгольм
| ||||
| Триест | | |||
| Руан | | |||
| | |
Итак, заполнены пять клеток таблицы, соответствующие базисным переменным. Остальные четыре переменные являются небазисными и равны нулю (x12 = x31 = x13 = x23 = 0), т.е. при таком плане перевозок из Стокгольма в Лион и из Руана в Лейпциг холодильные установки не перевозятся, при этом из Стокгольма и Триеста вывозятся все установки, излишков не остается.
Получен допустимый план, который можно использовать в качестве опорного и начать с него решение задачи. Впоследствии от этого плана мы будем переходить к другим, более дешевым. Чтобы наглядно убедиться, что впоследствии мы получим более выгодные планы перевозок, можно подсчитать, во сколько обойдется оплата перевозок по плану, построенному МСЗУ. Для этого подставим его в целевую функцию задачи: 25x11 + 14x12 +
+ 18x21 + 8x22 + 12x31 + 6x32 = 25*120 + 18*30 + 8*10 + 6*80 = 4100 (ф.ст.)
Метод наименьшей стоимости
Недостатком метода северо-западного угла является то, что при построении исходного опорного плана никак не учитываются коэффициенты целевой функции. Если бы удалось их учесть, то можно было бы сразу построить более дешевый план. Тогда в ходе решения можно было бы быстрее перейти к самому дешевом, т.е. оптимальному плану. Существуют методы, позволяющие сразу построить этот план таким образом, что значение целевой функции на нем будет ближе к искомому оптимуму.
Один из них - метод наименьшей стоимости, который для задачи на минимум применяют следующим образом. Строят такую же таблицу, как и при использовании МСЗУ, но указывают в ней коэффициенты целевой функции для каждой ячейки. Таблицу начинают заполнять с той ячейки, которой соответствует наименьший коэффициент cij., т.е. вначале отправляют продукцию по тому направлению, где перевозки самые дешевые.
Пусть наименьшая цена перевозки соответствует переменной xiojo. Тогда
1). Если aio < bjo, то xiojo = aio.
После этого строку io исключают из рассмотрения (все xioj = 0), а первому столбцу вместо bjo ставят в соответствие bjo`= bjo - aio.
2). Если aio > bjo , то xiojo = bjo. Исключают столбец jo, aio`= aio - bjo.
3). Если aio = bjo, то можно исключить либо столбец, либо строку.
Затем снова выбирают наименьший коэффициент cij из оставшихся и рассматривают соответствующую ячейку.
Если клеток с наименьшим коэффициентом несколько, то берется та из них, которой можно присвоить наибольшее значение; если и таких несколько, то любая из них.
Далее действуют аналогично, пока не будут исключены из рассмотрения все клетки таблицы. Если при этом заполнены менее чем
m+n-1 клетка таблицы, то вводят в базис со значением 0 переменную, которой соответствует наименьший коэффициент cij из незаполненных клеток.
Рассмотрим применение данного метода к той же задаче. В левый верхний угол каждой клетки таблицы впишем значения коэффициентов целевой функции при переменных. Наименьшие коэффициенты, равные нулю, находятся в третьем столбце (при трех переменных - x13, x23, x33). Какую из них выбрать? Если сравнивать запасы и потребности, оказывается, что в любом центре производства производится больше установок, чем необходимо дополнительному центру сбыта. Следовательно, при выборе любой из этих переменных ее нужно приравнять к 10. Возьмем, например, переменную x13, т.е. излишек установок в Стокгольме. Так как 120 > 10
(a1 > b3), будем считать, что все 10 «лишних» установок производятся именно в Стокгольме и там останутся (x13 = 10). После этого дополнительный центр сбыта можно исключить из рассмотрения, а из Стокгольма останется вывезти еще 110 установок:

| Лейпциг | Лион | дополнительный центр сбыта | ai |
| Стокгольм | | |||
| Триест | ||||
| Руан | ||||
| bj | 150 |
Теперь наименьший коэффициент, равный 6, соответствует стоимости перевозки одной установки из Руана в Лион. В Руане производится столько же установок, сколько необходимо поставить в Лион, поэтому x32 = 90, а из рассмотрения можно исключить либо третью строку, либо второй столбец. Исключим из рассмотрения Руан, а новые потребности Лиона примем равными нулю:

| Лейпциг | Лион | дополнительный центр сбыта | ai |
| Стокгольм | | |||
| Триест | ||||
 Руан Руан
| ||||
| bj | 150 | |
В оставшейся части таблицы дешевле всего поставки из Триеста в Лион (min {25; 14; 18; 8} = с22 = 8), но их следует принять равными нулю
(x22 = 0), так как потребности Лиона уже полностью удовлетворены. После этого в рассмотрении останутся только поставки в Лейпциг из Стокгольма и Триеста. Везти установки из Триеста дешевле (с21 = 18), и эти перевозки следует принять равными 40 (x21 = 40). Оставшиеся в Стокгольме
110 установок поставляются в Лейпциг (x11 = 110):
 
| Лейпциг | Лион | дополнительный центр сбыта | ai |
| Стокгольм | | |||
 Триест Триест
| ||||
 Руан Руан
| ||||
| bj | | |
Заполненные 5 клеток таблицы соответствуют базисным переменным опорного плана. Отметим, что здесь базис вырожденный [3], так как одна из базисных переменных (x22) равна нулю. Полученный таким способом план несколько дешевле, чем план, полученный методом северо-западного угла: 25*110 + 18*40 + 6*90 = 4010 < 4100. Можно предположить, что если начать решать задачу с этого плана, то оптимальный план будет получен быстрее.
Если транспортная задача поставлена на максимум, а не на минимум, то рассмотренный метод превращается в метод наибольшей стоимости, и заполнение таблицы начинают с той ячейки, в которой коэффициент целевой функции – самый большой.
Метод аппроксимации Фогеля
Еще более близкий к оптимальному план может быть получен с использованием метода аппроксимации Фогеля.
Этот метод принято сокращенно обозначать МАФ.
Метод является эвристическим, т.е. интуитивным, не обоснованным строго. Следует отметить, что во многих случаях план, полученный с его помощью, совпадает с тем, который получается при использовании метода наименьшей стоимости.
Алгоритм метода состоит в следующем:
1). Рассматривая матрицу затрат на перевозки, вычисляют штрафы для строк и столбцов, вычитая наименьший элемент строки (столбца) из следующего за ним по величине элемента этой же строки (столбца).
2). Выбирают столбец (строку) с наибольшим штрафом (если их несколько, то любой(-ую) из них). В нем (ней) выбирают клетку с наименьшим коэффициентом целевой функции и заполняют ее (алгоритм заполнения, пересчета свободных членов и исключения строки (столбца) такой же, как и в ранее рассмотренных двух методах).
3). Для оставшихся столбцов (строк) с ненулевыми свободными членами снова вычисляют штрафы и возвращаются к пункту 2, и так пока все клетки не будут исключены из рассмотрения.
4). Если из рассмотрения не исключены только столбцы (строки) с нулевыми свободными членами, к ним применяют метод наименьшей стоимости.
Для рассматриваемого примера наибольшим штрафом будет 14 – для Стокгольма. Из этого центра производства дешевле всего поставлять продукцию в дополнительный центр сбыта (не поставлять никуда) - с13 = 0. Поэтому примем x13 = 10:
 |
| Лейпциг | Лион | дополнительный центр сбыта | ai | штраф | |
| Стокгольм | | 14-0=14 | |||
| Триест | 8-0=8 | ||||
| Руан | 6-0=6 | ||||
| bj | 150 | ||||
| штраф | 18-12=6 | 8-6=2 | 0-0=0 |
При пересчете штрафов оказывается, что наибольший снова соответствует Стокгольму. Теперь из него дешевле всего поставлять продукцию в Лион, и эти поставки следует принять равными 90 (x12 = 90):
 |

| Лейпциг | Лион | дополнительный центр сбыта | ai | штраф |
| | 25-14= | ||||
| Стокгольм | | =11 | |||
| Триест | 18-8=10 | ||||
| Руан | 12-6=6 | ||||
| bj | 150 | ||||
| штраф | 18-12=6 | 8-6=2 |
Наибольший штраф (25) по-прежнему в первой строке. Следовательно, оставшиеся в Стокгольме 20 установок будут перевезены в Лейпциг (x11 = 20). После этого наибольший штраф будет соответствовать Триесту, откуда следует перевезти 40 установок в Лейпциг (x21 = 40). Недостающие после этого в Лейпциге 90 установок будут поставлены из Руана (x31 = 90):
 
| Лейпциг | Лион | дополнительный центр сбыта | ai | штраф |
| | |||||
  Стокгольм Стокгольм
| | ||||
| Триест | |||||
| Руан | |||||
| bj | | ||||
| штраф | 18-12=6 |
Подставив полученный план в целевую функцию, легко убедиться, что он еще дешевле – 3560 ф.ст. Более того, как будет показано в дальнейшем, этот план является и оптимальным, т.е. в данном случае методом аппроксимации Фогеля сразу получено решение задачи, что для задач небольшой размерности случается очень часто. Однако, в общем случае это не так, и оптимальное решение следует искать методом потенциалов.
Можно доказать, что план, построенный любым из трех перечисленных методов, будет действительно опорным (т.е. что систему ограничений можно привести к такому виду, что столбцы коэффициентов при ненулевых переменных будут линейно независимы) [1, 14].
Метод потенциалов
Общим методом решения транспортных задач является метод потенциалов.
Рассмотрим закрытую модель транспортной задачи на минимум (n поставщиков и m потребителей). Поставим в соответствие каждому поставщику некоторое число ui,  , а каждому потребителю - vj,
, а каждому потребителю - vj,  . Назовем эти числа потенциалами (по своему смыслу это переменные задачи, двойственной транспортной; ui соответствуют первой группе ограничений, а vj – второй [4, 5]).
. Назовем эти числа потенциалами (по своему смыслу это переменные задачи, двойственной транспортной; ui соответствуют первой группе ограничений, а vj – второй [4, 5]).
Если представить опорный план транспортной задачи в виде таблицы, то каждой ячейке можно поставить в соответствие сумму потенциалов (сложить потенциалы, соответствующие строке и столбцы, на пересечении которых находится эта ячейка). Кроме того, каждой ячейке соответствует коэффициент целевой функции. Применяя метод потенциалов, мы будем сравнивать эти коэффициенты с суммами потенциалов.
Метод потенциалов решения транспортной задачи основан на двух теоремах [1, 12, 14], которые здесь приводятся без доказательства:
Теорема об изменении плана транспортной задачи.
Условие теоремы: пусть Хо, Х1 - опорные планы. Для всех базисных компонент первого из них сумма потенциалов равна коэффициенту целевой функции (т.е. если переменная xijо – базисная, то cij = ui + vj). Во втором плане Х1 все номера базисных компонент те же, кроме одной (т.е. при переходе от первого плана ко второму одна переменная из базиса вышла, а другая вошла). При этом для новой базисной переменной xi1j1, сумма потенциалов больше коэффициента целевой функции (ci1j1 < ui1 + vj1).
Утверждение теоремы: тогда новый план дешевле или по крайней мере не дороже (т.е.  - при переходе к плану Х1 целевая функция не возрастает).
- при переходе к плану Х1 целевая функция не возрастает).
Замечание: можно доказать, что при этом значение целевой функции уменьшится на xi1j11(ui1 + vj1 - сi1j1). В этом произведении второй сомножитель – обязательно положительный по условию теоремы, а вот первый может быть нулевым, если опорный план – вырожденный. Поэтому в случае вырожденности опорных планов (если xi1j11 = 0) значение целевой функции может не измениться.
На рисунке 1 серым цветом условно обозначены заполненные ячейки таблицы, т.е. базисные компоненты плана. Стрелкой показано, какая переменная вышла из базиса, и какая вошла. Если при переходе от первого плана ко второму выполнилось условие теоремы, то был получен план, который стоит дешевле (не дороже). Так, в результате последовательных переходов от одного плана к другому, в ходе решения будет получен оптимальный план.
| u1 | ||||||

| … | |||||
| ui1 | ||||||
| … | ||||||
| un | ||||||
| v1 | … | vj1 | … | vm |
| xi1j11 | ||||||
Рисунок 1 – Иллюстрация к теореме об изменении плана
транспортной задачи
Чтобы определить, в какой момент это произойдет, применяют следующую теорему.
Теорема о критерии оптимальности транспортной задачи.
Пусть существует опорный план, для всех компонент которого сумма потенциалов не больше коэффициента целевой функции (т.е. ui + vj  cij
cij  i,j). Причем для базисных компонент этого плана имеет место строгое равенство: ui + vj = cij. Тогда это оптимальный план.
i,j). Причем для базисных компонент этого плана имеет место строгое равенство: ui + vj = cij. Тогда это оптимальный план.
Сам метод потенциалов представляет собой итерационный (т.е. основанный на последовательном использовании результатов предыдущих вычислений) процесс пересчета элементов таблицы. Он включает следующие этапы.
1. Строится опорный план транспортной задачи. Это можно сделать любым из рассмотренных выше способов.
2. Для базисных элементов плана (т.е. заполненных клеток таблицы) формируется система уравнений {ui + vj = cij с неизвестными ui и vj.
Осуществляют решение этой системы. В этой системе (m+n–1) уравнение на (m+n) переменных, и она имеет бесконечное множество решений. Находят хотя бы одно решение.
3. Находят суммы потенциалов (ui + vj) для всех клеток таблицы. Они сравниваются с коэффициентами целевой функции cij также для всех клеток таблицы: {ui + vj  cij.
cij.
Если это верно, то имеющийся план оптимален (по соответствующей теореме).
Если это не так, то находят ту клетку, для которой сумма потенциалов больше коэффициента целевой функции, т.е. (i1,j1): ui1 + vj1 > ci1j1
4. На основе (i1,j1) строится цикл пересчета плана.
Циклом пересчета плана называется замкнутая ломаная, каждая вершина которой лежит в одной из клеток таблицы, причем одна в пустой, а остальные в заполненных. Звенья ломают горизонтально или вертикально.
Можно доказать, что цикл можно построить (причем единственный) для любой пустой клетки.
Возможно самопересечение цикла. Пример самопересечения представлен на рисунке 2. На этом рисунке пять из шести вершин цикла находятся в заполненных ячейках (темных), а одна – в пустой. При этом звенья цикла пересекают друг друга (вершины в этом пересечении нет).
Построение цикла необходимо для того, чтобы построить следующий план допустимым.
5. Осуществляют разметку цикла следующим образом: в пустой клетке ставят знак «+», а затем помечают вершины цикла, чередуя знаки «-» и «+» (поскольку число клеток четное, направление безразлично).
6. Определяют величину пересчета плана, как наименьшее число из всех базисных компонент, помеченных знаком «-».
7. Строится новый опорный план следующим образом: в пустой клетке ставят число, равное величине пересчета плана - эта компонента входит в базис. К остальным вершинам цикла прибавляют или вычитают эту величину в зависимости от того, каким знаком они помечены. Компонента, соответствующая той клетке, в которой стояло это число, выходит из базиса, становится равной нулю. Если минимум (величина пересчета плана) достигается в нескольких клетках, то одну из этих клеток оставляют пустой, а в остальных ставят нули (имеет место вырожденный базис).
Затем возвращаются к пункту 2.

| ||
Рисунок 2 – Самопересечение цикла
Сходимость процесса основана на том, что переход к новым опорным планам осуществляют таким образом, что согласно теореме об изменении плана на каждом шаге процесса значение целевой функции уменьшается, а она ограничена снизу.
Отметим, что для того, чтобы п
Последнее изменение этой страницы: 2016-08-11
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...